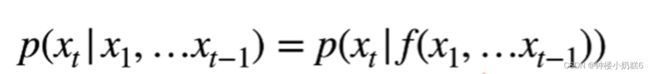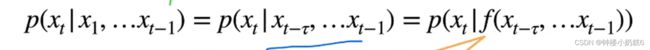深度学习——序列模型（笔记）

1.序列数据：

①现实生活中有很多数据是有时序结构，比如电影的评分随时间的变化而变化。

②统计学中，超出已知观测范围进行预测是外推法，在现有的观测值之间进行估计是内插法

 

2.统计工具：处理序列数据选用统计工具和新的深度神经网络架构

①在时间t观察到xt,那么得到T个不独立的随机变量

（x1…xT）~p(x)

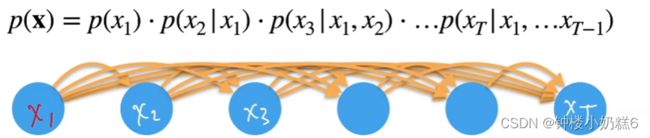
②使用条件概率展开

p(a,b)=p(a)p(b|a)=p(b)p(a|b)

注：

①p(b|a)是a发生前提下b发生概率,即如果已知a发生了,则b发生的概率

②不独立的随机变量：变量之间存在某种关联

 表示从x1一直到xT的方向，想要知道时序序列T时刻发生的事情：T时刻之前所有时刻发生的事情

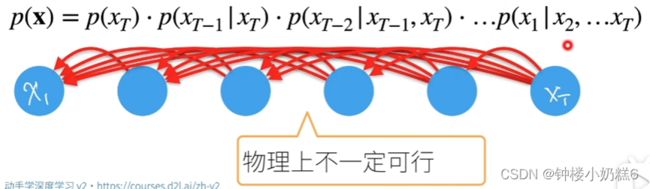
 表示先计算xT在依次计算到x1，反序。已知未来T时刻发生的事情，反推过去时刻发生的事情，物理上不一定可行。

3.序列模型

 ①对条件概率建模

对见过的数据建模，也称自回归模型：有一些数据，预测数据的时候，使用的是本数据样本而不是其他数据。

可以对t时刻之前的数据进行建模，使用自回归模型（给定一些数据，预测数据的时候使用的是本数据样本，而不是其他数据），表示成一个函数，可以看作是机器学习模型，在t时刻之前的数据上进行训练，然后取预测t时刻的数据。

4.各个方案

方案A—马尔科夫假设

 ①假设当前的数据只跟τ个过去数据点相关

 

 假设τ=2，只跟前面2个数据相关，第3个是预测的值。所以每预测一个新数据，只需要看过去τ个数据就可以。τ越小模型简单，τ的值是固定的，不会随着时间的增大而增大（过去预测的时间越长，关联程度小）

 例如在过去数据上训练一个MLP模型

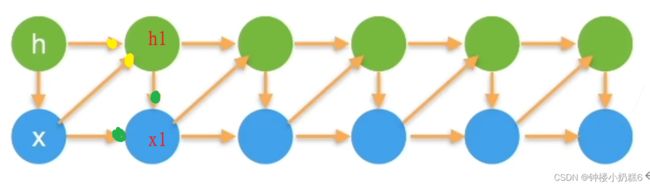
方案B-潜变量模型

 

①引入潜变量ht来表示过去信息ht=f(x1,…, xt-1)  这样xt=p(xt|ht)

引入了潜变量h,h是不断更新的。h和前一个时刻的h和x相关。等价于两个模型：一个模型是根据前一个时刻的潜变量h和x，重新计算h1。第二个模型是根据潜变量h1，和x计算x1。拆分成两个模型，每个模型和1个或2个相关，计算容易。

 【总结】

①时序模型中，当前数据跟之前观察到的数据相关

②自回归模型使用本身过去的数据去预测未来

③马尔科夫模型假设当前只跟最近少数数据相关，从而简化模型

④潜变量模型使用潜变量来概括历史信息。

【代码实现】

1.# 使用正弦函数和一些可加性噪声来生产序列数据，时间步为1，2，...1000

import torch
from torch import nn
from d2l import torch as d2l

# 使用正弦函数和一些可加性噪声来生产序列数据，时间步为1，2，...1000
T = 1000
time = torch.arange(1, T + 1, dtype=torch.float32)  # time:1~1000
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

2.

# 马尔可夫假设 将数据映射为数据对yt=xt  feature-label对
# 从第五个时刻开始，每个时刻的label是该时刻的x值。该时刻的输入是前4个时刻的整体向量，训练数据996个4维数据
# 以4为长度并且滑动，每4个为特征，第5个是标签

tau = 4
features = torch.zeros((T - tau, tau))  # 996*4个训练数据
# 每4个为特征，第5个是标签
for i in range(tau):  # i取值0-3
    features[:, i] = x[i:T - tau + i]
labels = x[tau:].reshape((-1, 1))

batch_size, n_train = 16, 600  # 使用600个特征-标签对进行训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                            batch_size, is_train=True)

3.使用一个简单的结构：拥有两个全连接层的多层感知机

# 初始化网络权重函数
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform(m.weight)


# 多层感知机
def get_net():
    net = nn.Sequential(nn.Linear(4, 10), nn.ReLU(), nn.Linear(10, 1))
    net.apply(init_weights)
    return net


loss = nn.MSELoss()

4.训练

# 训练
def train(net, train_iter, loss, epochs, lr):
    trainer = torch.optim.Adam(net.parameters(), lr)
    for epoch in range(epochs):
        for x, y in train_iter:
            trainer.zero_grad()
            l = loss(net(x), y)
            l.backward()
            trainer.step()
        print(f'epoch {epoch + 1}, '
              f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')


net = get_net()
train(net, train_iter, loss, 5, 0.01)

5.单步预测，检查模型预测下一个时间步的能力

onestep_preds = net(features)
d2l.plot([time, time[tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
         'x', legend=['data', '1-step preds'], xlim=[1, 1000],
         figsize=(6, 3))

6.多步预测

multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
    multistep_preds[i] = net(
        multistep_preds[i - tau:i].reshape((1, -1)))

d2l.plot([time, time[tau:], time[n_train + tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy(),
          multistep_preds[n_train + tau:].detach().numpy()], 'time',
         'x', legend=['data', '1-step preds', 'multistep preds'],
         xlim=[1, 1000], figsize=(6, 3))

7.K步预测

max_steps = 64

features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i（i=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)

steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
         [features[:, tau + i - 1].detach().numpy() for i in steps], 'time', 'x',
         legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
         figsize=(6, 3))