DBNet学习笔记

1 概述

搞懂了DBNet的二值化处理和标签制作就理解了DBNet网络。

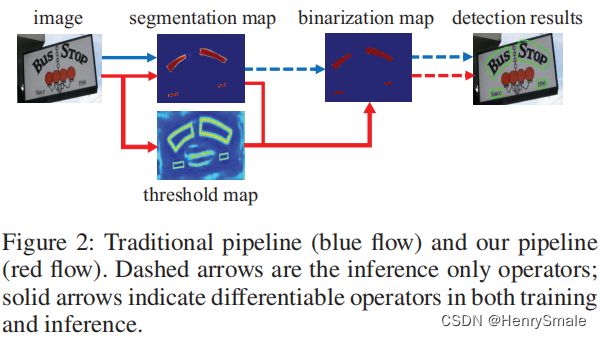
1.1 传统方法和DBNet的比较

传统分割算法流程（蓝色箭头部分）：

• 先通过网络输出文本分割的概率图；
• 然后使用设定阈值将概率图转化为二值图；
• 最后通过后处理得到检测结果（文本框坐标）。
• 缺点：在于阈值的选取非常困难。

DBNet提出可微分二值化（红色箭头部分）来解决这个缺点：

• 对每一个像素点进行自适应二值化；
• 二值化阈值由网络学习得到，彻底将二值化这一步骤加入到网络里一起训练，这样最终输出的阈值图就非常鲁棒。

1.2 DBNet网络结构

DBNet网络结构主要由3个模块构成，分别说明如下。
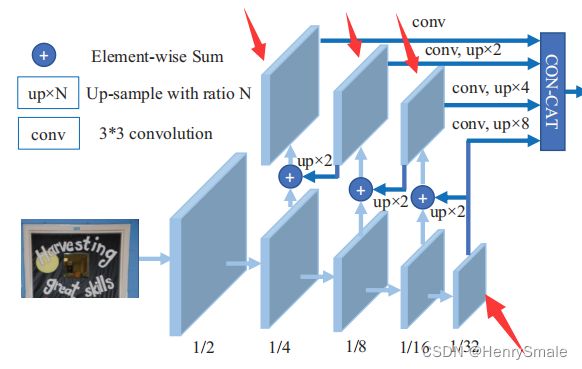
（1）模块1（FPN 结构）：分为自底向上的卷积操作与自顶向下的上采样，以此来获取多尺度的特征

• 主干网络是ResNet，在stage2-4中使用Deformable convolution来更好地检测长文本；

• 1 图下半部分是 $3\times 3$ 的卷积操作，分别获取原图大小比例的 1/2、1/4、1/8、1/16、1/32 的特征图；

• 然后自顶向下进行上采样 $\times 2$，然后与自底向上生成的相同大小的特征图融合得到1图的上半部分；

• 融合之后再采用$3\times 3$ 的卷积消除上采样的混叠效应；

• 经过FPN后，得到了四个大小分别为原图的1/4，1/8，1/16，1/32的特征图;
  

• 将四个特征图分别上采样，统一为 1/4 大小的特征图；

• 最后将四个1/4大小的特征图concat，得到F。

问：如何进行concat？
答：我估计是四个特征图对应像素点进行平均，具体如何concat，建议去看源代码。

（2） 模块2（FCN 网络结构）：获取概率图 P 和阈值图 T

• 将 1/4 大小的特征图经过一系列卷积和转置卷积的操作后，生成与原图一样大小的概率图 P 和阈值图 T。

1         binary = self.binarize(fuse)   #由F得到P,输入fuse代表F
2         if self.training:
3             result = OrderedDict(binary=binary)
4         else:
5             return binary #如果在推理阶段，直接用P得到文本框
6         if self.adaptive and self.training: #如果在训练阶段且自适应阈值，则计算threshold map
7             if self.serial:
9                 fuse = torch.cat(
10                        (fuse, nn.functional.interpolate(
11                            binary, fuse.shape[2:])), 1)
12            thresh = self.thresh(fuse) #由F得到T，self.thresh与self.binarize实现一样，只是训练得到的参数不同。

self.binarize函数具体实现如下：

1         self.binarize = nn.Sequential(
2             nn.Conv2d(inner_channels, inner_channels //
3                       4, 3, padding=1, bias=bias),   #shape:(batch,256,1/4W,1/4H)
4             BatchNorm2d(inner_channels//4),
5             nn.ReLU(inplace=True),  
6             nn.ConvTranspose2d(inner_channels//4, inner_channels//4, 2, 2), #shape:(batch,256,1/2W,1/2H)
7             BatchNorm2d(inner_channels//4),
8             nn.ReLU(inplace=True),
9             nn.ConvTranspose2d(inner_channels//4, 1, 2, 2),  #shape:(batch, W, H)
10            nn.Sigmoid())

流程如下：

• 1）F（shape:(batch,256,1/4W,1/4H)）–>shape:(batch,64,1/4W,1/4H)： 先经过卷积层，将通道压缩为输入的1/4，然后经过BN和relu，得到的特征图shape；（代码2至5行）
• 2）shape:(batch,64,1/4W,1/4H)–> shape:(batch,256,1/2W,1/2H)：将得到的特征图进行反卷积操作，卷积核为(2,2)，得到的特征图shape为(batch,256,1/2W,1/2H)，此时为原图的1/2大小；（代码第6行）
• 3） shape:(batch,256,1/2W,1/2H)–>shape:(batch,W,H)：再进行反卷积操作，同第二步，不同的是输出的特征图通道为1，得到的特征图shape为(batch,W,H)，此时为原图大小。（代码第9行）
• 4）shape:(batch,W,H)–>[0,1]：最后经过sigmoid函数，输出概率图，probability map。（代码第10行）

（3）模块3（DB操作）：获取近似二值图

• 将概率图 P 和阈值图 T 经过 DB （可微二值化）操作，得到近似二值图。

thresh_binary = self.step_function(binary, thresh) #binary和thresh分别为P和T，thresh_binary为近似二值图

def step_function(self, x, y):
	return torch.reciprocal(1 + torch.exp(-self.k * (x - y)))

利用上面三个模块，可以得到概率图、阈值图和近似二值图。
训练过程对这三个图进行监督学习，更新各个模块的参数。
推理过程直接使用概率图，然后使用固定阈值获取结果。

2 二值化

2.1 标准二值化

在传统的图像分割算法中，我们获取概率图后，会使用标准二值化（Standard Binarize）方法进行处理，将低于阈值$t$的像素点置0，高于阈值$t$的像素点置1：
$$B_{i,j}=\{\begin{array}{c}1,\text{if}{P}_{i,j}\ge t,\\ 0,\text{otherwise.}\end{array}$$
标准的二值化是不可微的，无法放入到网络中进行优化学习。

2.2 可微二值化

可微二值化就是将标准二值化中的阶跃函数进行了近似：
$${\hat{B}}_{i,j}=\frac{1}{1+e^{-k(P_{i,j}-T_{i,j})}},$$
$k$ 是膨胀因子（经验型设置为50）。
可微二值化本质上是一个 带系数 $k$ 的 sigmoid 函数，取值范围为(0,1)；$P_{i,j}$指概率图像素点，$T_{i,j}$指阈值图像素点。

2.3 SB和DB曲线

标准二值化和可微二值化的对比如图 (a) 所示，$x>0$属于正样本（文字区域），$x<0$属于负样本（非文字区域）。
SB 代表标准二值化曲线，DB 代表可微二值化曲线，可以看到曲线变得更为平滑，也就是可微：

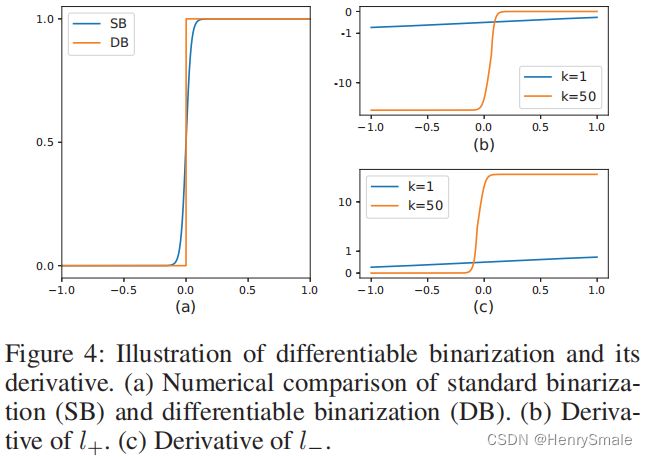
除了可微之外，DB 方法也会改善算法的性能，在反向传播是梯度的计算上进行观察。当使用交叉熵损失（$y=1$代表文字区域）时，正负样本的 loss 分别为 $l_{+}$ 和 $l_{-}$，公式如下：

• 交叉熵损失函数: $L=-[y\log \hat{B}+(1-y)\log (1-\hat{B})]$
• 正样本 ($y=1$) 损失: $l_{+}=-\log \left(\frac{1}{1+e^{-k\left(P_{i,j}-T_{i,j}\right)}}\right)$
• 负样本 ($y=0$) 损失: $l_{-}=-\log \left(1-\frac{1}{1+e^{-k\left(P_{i,j}-T_{i,j}\right)}}\right)$

对输入 $x=P_{i,j}-T_{i,j}$ 求偏导，令$f(x)=\frac{1}{1+e^{-kx}}$，则会得到：
$$\begin{array}{c}\frac{\delta l_{+}}{\delta x}=-kf(x)e^{-kx}\\ \frac{\delta l_{-}}{\delta x}=-kf(x),\end{array}$$
分析图(b)和©，可以得到如下一些结论：

• 增强因子$k$会使得错误预测对梯度的影响变大，从而促进模型的优化过程，产生更为清晰的预测结果；
• 图(b)为$l_{+}$的导数曲线，如果发生误报（正样本被预测为负样本$x<0$），图(b)小于 0 的部分导数非常大，证明损失也是非常大的，则更能清晰的进行梯度回传。
• 图©为$l_{-}$的导数曲线，当发生误报（负样本被预测为正样本$x>0$），导数也是非常大的，损失也比较大。

3 构建真实标签

在训练DBNet的时候，需要概率图$G_s$、阈值图$G_d$及近似二值图作为监督信息（ground-truth）:

• 概率图：每个像素点的值表示该位置属于文本区域的概率；
• 阈值图：每个像素点的值表示该位置的二值化阈值；
• 近似二值图：每个像素点的值为 0 或 1，利用概率图和阈值图通过 DB 算法计算得到。

因为近似二值图可以由概率图和阈值图计算得到，所以只需要构建阈值图和概率图两个标签。
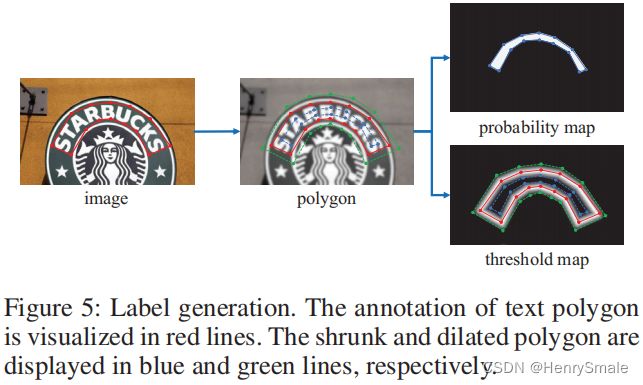
阈值图和概率图：参考 PSENet 中的方法，使用扩张和收缩的方式；在该方法中，对于一幅文字图像，文本区域的每个多边形使用一组线段$G={\left\{S_k\right\}}_{k=1}^n$来进行描述， $n$为线段个数。

3.1 概率图$G_s$和近似二值图的标签构建方法

• 概率图和近似二值图：使用收缩的方式（Vatti clipping算法）构建标签；
• 标签为：蓝线区域内为文字区域，蓝线区域外为非文字区域；
• 将原始的多边形文字区域$G$（红线区域）收缩到$G_s$（蓝线区域），收缩的偏移量$D$按照如下公式计算：
  $$D=\frac{A\left(1-r^2\right)}{L},$$
  其中：
  – $L$：多边形的周长；
  – $A$：多边形的面积；
  – $r$：收缩因子，经验设置为 0.4。

问题：原始的多边形文字区域$G$（红线区域）是怎么得到的？

3.2 阈值图$G_d$的标签构建方法

• 类似于概率图$G_s$和近似二值图的标签构建过程，为阈值图生成标签；
• 首先将原始的多边形文字区域$G$扩张到$G_d$（绿线区域），偏移量$D$同概率图中的$D$；
• 将收缩框$G_s$（蓝线）和扩张框$G_d$（绿线）之间的间隙视为文本区域的边界，计算这个间隙里每个像素点到原始图像边界$G$（红线）的归一化距离（最近线段的距离）；
• 计算完之后可以发现，扩张框$G_d$上的像素点和收缩框$G_s$上的像素点的归一化距离的值是最大的，并且文字红线上的像素点的值最小，为0。呈现出以红线为基准，向$G_s$和$G_d$方向的值逐渐变大。
• 所以再对计算完的这些值进行归一化，也就是除以偏移量$D$，此时$G_s$和$G_d$上的值变为1，再用1减去这些值;
• 最后得到，红线上的值为1，$G_s$和$G_d$线上的值为0；
• 呈现出以红线为基准，向$G_s$和$G_d$方向的值逐渐变小。此时$G_s$和$G_d$区域内的值取值范围为[0,1]；
• 最终再进行缩放，比如归一化到 [0.3，0.7]，这就是最终的标签。

有了标签，就可以进行监督学习啦！！

4 损失函数

损失函数为概率图的损失、二值化图的损失和阈值图的损失的和：
$$L=L_s+\alpha \times L_b+\beta \times L_t$$
其中：

• $L$为总的损失；
• $L_b$为近似二值图的损失，使用 Dice 损失（二元交叉熵）；
• $L_s$为概率图损失，为平衡正负样本的比例，使用带 OHEM 的 Dice 损失进行困难样本挖掘，正样本:负样本=1:3；
• $L_t$为阈值图损失，使用预测值和标签间的 $L_1$ 距离；
• $\alpha$ 和 $\beta$ 为权重系数，分别设置为1和10。

$$L_s=L_b=\sum _{i\in S_l}{y}_i\log x_i+\left(1-y_i\right)\log \left(1-x_i\right),$$
其中$S_l$表示使用OHEM进行采样，正负样本比例为1:3。
$L_t$计算预测值和标签间的 $L_1$ 距离：
$$L_t=\sum _{i\in R_d}\left|y_i^{\ast }-x_i^{\ast }\right|$$