机器人系统辨识——基于MATLAB的非线性系统辨识

Hello，欢迎做客我的博客。
这里会介绍关于机器人的方方面面，希望对你有所帮助。
今天的内容关于机器人动力学模型的参数辨识，这是在做机器人控制前的关键一步！

工具和参考链接

由于机器人动力学模型往往都是非线性的，这里用到的工具是：

MATLAB的System Identification Toolbox（系统辨识工具箱），其中的Nonlinear Grey-Box Models（非线性灰箱建模工具），链接如下：

System Identification Toolbox

Nonlinear Grey-Box Models

主要的参考示例：
Modeling an Industrial Robot Arm

1 机器人动力学模型

在对模型参数进行辨识之前，首先需要对机器人进行建模，建模的方法通常是牛顿欧拉法或者拉格朗日方法。关于建模的部分，读者可以参考我之前的博客。如：
机器人动力学建模之牛顿欧拉法推导

此处，直接给出机器人的非线性动力学模型如下：
$$\begin{array}{rl}{\dot{x}}_1& =K_a\sin x_2\\ {\dot{x}}_2& =K_b{x}_3^2\\ {\dot{x}}_3& =u\\ y_1& =x_1\\ y_2& =x_2\\ y_3& =x_3\end{array}$$
其中，$x$代表状态，$u$代表输入，$y$代表输出。
$K_a$和$K_b$为待辨识参数。

2 辨识前的准备——采集实验数据

在进行参数辨识前，我们需要采集输入和输出数据，即给定一组$u$，然后记录系统的$y$。通常，我们可以让$u$是正弦信号，或者多个正弦信号的叠加，以获得更好的辨识效果。

通常来说，我们需要通过实验去采集数据。

在这里，我们的目的是介绍MATLAB系统辨识工具箱的用法，为了更加直观的看出系统辨识的效果，我们可以基于上述动力学模型生成一组数据，来检验MATLAB的系统辨识效果。

数据生成程序：

clc;
clear all;
close all;

period = 0.01; % 注意这里是采样时间
T = 10;

% 参数设置
Ka = 1.21;
Kb = -0.6;

x1 = 0;
x2 = 0;
x3 = 0;

Input = [];
Output = [];

for t = 0:period:T
    % 给定输入，正弦函数
    u = sin(2*pi/10*t);
    % 系统动力学模型迭代
    x1_p = x1 + Ka*sin(x2)*period;
    x2_p = x2 + Kb*x3^2*period;
    x3_p = x3 + u*period;
    x1 = x1_p;
    x2 = x2_p;
    x3 = x3_p;
    % 输出
    y1 = x1;
    y2 = x2;
    y3 = x3;
    % 保存数据
    Input = [Input; u];
    Output = [Output; y1,y2,y3];
end

% 保存数据
save('blogexample.mat', 'Input', 'Output');

注意，这里我们设置了$K_a=1.21$以及$K_b=-0.6$。下面，我们可以看看MATLAB是否能辨识得到这组参数。

3 系统辨识——MATLAB代码示例

利用MATLAB进行系统辨识的步骤分为两步：

• 定义模型文件（定义机器人动力学模型）
• 设置辨识过程（）

3.1 模型文件

程序如下：

function [dx, y] = blogmodel_m(t, x, u, Ka, Kb, varargin)
%% 函数的参数dx，y，t，x，u不可更改
%% 函数参数Ka，Kb即为待辨识参数
  % 输出方程
  y = [x(1); x(2); x(3)];
  % 动力学模型（微分方程），dx即为x的导数
  dx = [Ka*sin(x(2)); ...
        Kb*x(3)^2; ...
        u];
end

3.2 定义辨识过程

整个辨识过程主要用到四个函数：

• idnlgrey：生成一个系统辨识对象（包含了系统模型，输入，状态，输出向量等等信息）
• iddata：将数据打包为iddata格式，便于系统辨识工具箱使用
• nlgreyest：系统辨识函数（主要函数，执行的就是优化参数的过程）
• compare：对比真实输出和模型输出的结果

下面是详细程序以及注释：
程序如下：

clc;
clear all;
close all;

%% 配置模型
FileName     = 'blogmodel_m';               % 模型文件.
Order        = [3 1 3];                     % 输出、输入和状态向量的维数 [ny nu nx].
Parameters   = [1, -1]';                    % 待辨识参数的初始值
InitialStates = zeros(3, 1);                % 系统状态的初始值
Ts            = 0;                          % Time-continuous system.
% 生成一个系统辨识对象
nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ...
                        'Name', 'Blog Example Model', ... % 定义对象的名称
                        'InputName',  {'Voltage'}', ... % 定义输入向量的名称
                        'InputUnit', {'V' }', ... % 定义输入向量的单位
                        'OutputName', {'Position' 'Velocity' 'Acceleration'}', ... % 定义输出向量的名称
                        'OutputUnit', {'m' 'm/s' 'm/s^2'}', ... % 定义输出向量的单位
                        'TimeUnit', 's'); % 定义时间的单位
% 设置系统状态向量的名称和单位            
nlgr = setinit(nlgr, 'Name', {'Position' 'Velocity' 'Acceleration'}');
nlgr = setinit(nlgr, 'Unit', {'m' 'm/s' 'm/s^2'}');
% 设置待辨识参数的名称
nlgr = setpar(nlgr, 'Name', {'Ka : coeff 1' 'Kb : coeff2' });
nlgr.Parameters(1).Fixed = false; % 将参数1设置为可变参数，默认即为可变参数，若设置为固定参数，则优化时，该参数不变
nlgr.Parameters(1).Minimum = -10; % 设置参数1的下界为-10
nlgr.Parameters(1).Maximum = 10;  % 设置参数1的上界为10
% 打印出nlgr的信息
present(nlgr)

%% 导入数据
dataset = load('blogexample.mat');
z = iddata(dataset.Output, dataset.Input, 0.01, 'Name', 'Actual Data'); % 将数据打包为iddata格式，注意这里面的0.01代表了数据采样时间为0.01秒
z.InputName = {'Voltage'}; % 定义输入向量的名称
z.InputUnit = {'V' }; % 定义输入向量的单位
z.OutputName = {'Position' 'Velocity' 'Acceleration'}; % 定义输出向量的名称
z.OutputUnit = {'m' 'm/s' 'm/s^2'}; % 定义输出向量的单位
z.Tstart = 0; % 定义起始时刻
z.TimeUnit = 's'; % 定义时间单位

present(z);

%% 参数效果
X0init = zeros(3,1);
nlgr = setinit(nlgr, 'Value', num2cell(X0init)); % 设置状态向量的初始值
figure(1)
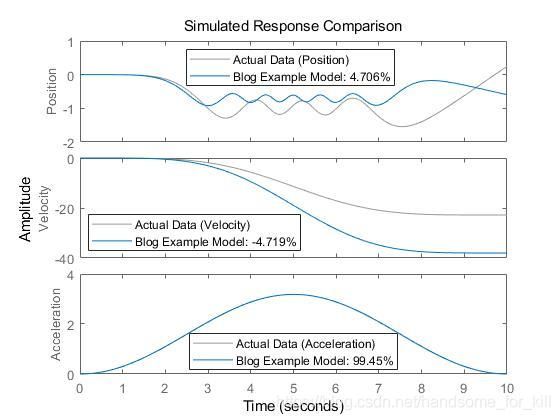
% 对比系统真实输出和模型输出（参数辨识前）
compare(getexp(z, 1), nlgr, [], compareOptions('InitialCondition', X0init)); 

%% 辨识系统参数
nlgr = nlgreyest(nlgr, getexp(z, 1), nlgreyestOptions('Display', 'on')); % 系统辨识
figure(2) 
% 对比系统真实输出和模型输出（参数辨识后）
compare(getexp(z, 1), nlgr, [], compareOptions('InitialCondition', X0init));

4 系统辨识结果

4.1 辨识前

4.2 辨识后

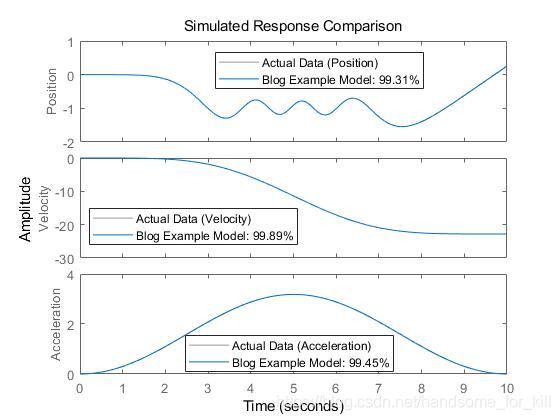
参数辨识的结果为：$K_a=1.211$和$K_b=-0.600$。和我们生成数据时设置的$K_a=1.21$以及$K_b=-0.6$几乎完全相同。

另外，从辨识结果也可以看到，参数辨识的效果相当只好。

5 更多

更多关于参数辨识过程的设置，比如优化算法，容许误差，可参考：
nlgreyestOptions

关于模型验证，参数辨识效果的展示，可参考：
Model Validation

关于本文的实例，大家可从下面链接中下载整理好的版本：
MATLAB参数辨识的小例子