DeepFM模型

在推荐系统中，学习特征的交互对于最大化CTR是非常重要的。尽管现有的方法都取得很大的成功，对于低阶和高阶的特征交互研究很少，还需要一些实验和特征工程。在本文中，我们展示了低阶和高阶交互的端对端学习。采用的模型是DeepFM，它将推荐系统的FM模型和深度模型进行整合。通过和谷歌的Wide&Deep模型对比，DeepFM的wide和deep部分共享输入，不需要对原始数据进行特征工程。基于bench-mark data和commercial data对DeepFM在CTR预估方面进行综合试验。

1.简介

在推荐系统中，CTR预估是非常重要的，它的任务就是估计用户点击推荐项目的概率。在许多推荐系统中，它们的目标就是最大化点击次数，通过CTR返回用户对物品的点击可能性的排序。在其他的一些应用领域，例如在线广告，它们的目标是提高广告收入，所以它们的策略调整为CTR×bid，其中，bid是用户每次点击所带来的收益。

学习用户的隐含交互特征对于CTR预估是非常重要的。在我们研究主流的app市场时发现，用户常在午餐时间下载有关外卖的app，表明app的种类和时间戳是CTR预估重要的信息。

另外，我们发现青少年男性喜欢射击游戏和角色扮演游戏，这表明app的种类、用户的性别、用户的年龄对于CTR预估是一个有用的信息。通常，用户低阶和高阶的交互特征在点击预估中扮演着重要的角色。

最有挑战性的在于寻找有效的交互特征。有些特征是根据专家的先验知识设计的，特别容易理解。有些交互特征隐藏在数据中，很难根据先验知识发现，这只能通过自动化学习捕获。。 即使对于易于理解的交互，专家似乎也不可能对它们进行详尽的建模，尤其是当功能数量很大时。

2.研究现状

FTRL是线性模型，不具备学习交叉特征能力。通常需要手工设计一些二阶交互特征，对于高阶特征的缺乏泛化能力。FM原则上可以进行高阶 交叉，考虑到计算的复杂性，在实际应用中，通常使用二阶交叉。

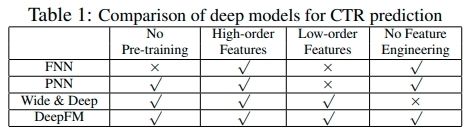
CNN更加偏向学习相邻特征的交互性，RNN对于点击存在序列依赖性。PNN和FNN很难捕捉低阶特征交互。Wide&Deep同时考虑了低阶和高阶的特征交互，在这个模型中，将线性模型（“wide”）和深度模型组合在一起。在这个模型中需要两部分输入，“wide part"和"deep part”，“wide part”特征工程部分以来专家经验。

我们可以发现，现存的模型偏好低阶、高阶特征的交互，或者依赖特征工程。在本文中，我们可以不需要任何特征工程，端对端学习所有不同阶特征交互。我们的主要贡献存在以下几点：

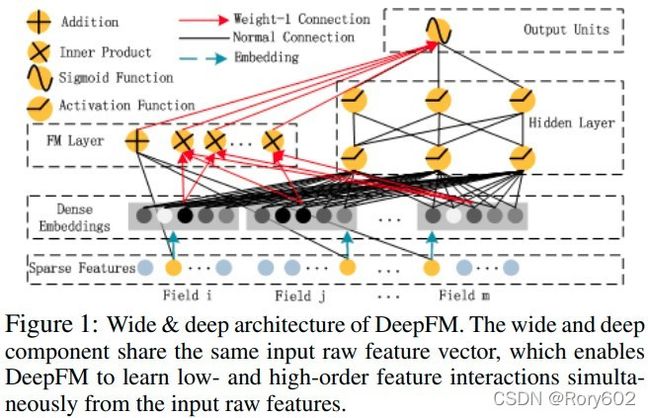
• 我们整合FM模型和DNN模型生成新的神经网络模型DeepFM（Figure 1），FM模型学习低阶特征的交互，DNN学习高阶特征交互。和Wide&Deep不同的是，DeepFM可以端对端训练，不需要进行特征工程。
• DeepFM由于它的“wide part”和“deep part”,模型的训练更加高效。
• 基于benchmark data和commercial data对DeepFM进行评估和现有的模型进行对比。

3.模型实现

假设我们的训练数据包含n个样本，$(\chi ,y)$ ，其中$\chi$是m-fileds数据，记录user和iterm，$y\in (0,1)$描述用户的点击行为，1表示用户点击item，否则是0。$\chi$ 可能包括类别变量和连续变量。类别变量进行onehot操作，数值变量不做改变，或者对数值变量进行离散化，然后进行onehot编码。然后每个样本可以用$(x,y)$表示，其中，$x=\left[x_{{\text{field}}_1},x_{{\text{field}}_2},\dots ,x_{{\text{filed}}_j},\dots ,x_{{\text{field}}_m}\right]$ 是一个多维向量，$x_{{\text{filed}}_j}$ 代表$\chi$的$j$ -th filed。通常来说，$x$ 是高维稀疏的。CTR预测就是建立$\hat{y}=CT{R}_{model}(x)$ 估计用户在给定背景（特征）情况下点击的概率。

3.1DeepFM

我们的目标是学习特征低阶和高阶的特征交互。如Figure 1所示，DeepFM有两个组件构成，FM部分和Deep部分，它们共享输入。对于特征$i$，$w_i$作为权重衡量特征一阶特征重要性，向量隐向量 $V_i$是衡量该特征和其他特征的交互影响。$V_i$喂给FM衡量二阶交互效应，同时喂给Deep部分用于衡量高阶交互效应。所有的参数，包括：$w_i,V_i$

和网络参数$(W^{(l)},b^{(l)})$在预测模型一起进行训练：
$$\hat{y}=sigmoid(y_{FM}+y_{DNN})(1)$$
其中，$\hat{y}\in (0,1)$是CTR预测值，$y_{FM}$是FM部分输出，$y_{DNN}$是深度部分的输出。

FM是在推荐系统中，用于学习特征交互的因子分解机。模型是由线性部分（一阶）和二阶特征交互组成，二阶特征交互是由两个隐向量内积表示。当特征稀疏的情况下，FM比之前的方法更能有效的捕捉二阶特征的交互效应。在之前的方法中，特征$i$和特征$j$只有在特征$i$和特征$j$都有记录的情况下才能学习。但是在FM模型中，可以通过隐向量$V_i$和$V_j$的内积衡量。由于这种弹性设置，当特征$i$或者特征$j$出现在数据记录中，FM模型可以训练隐向量$V_i(V_j)$。由于交互特征很少同时出现在训练数据中，通过FM模型可以更好的学习。

如Figure2所示，FM的输出是加法单元和内积单元的求和：
$$y_{FM}=⟨w,x⟩+\sum _{j_1=1}^d\sum _{j_2=j_1+1}^d⟨V_i,V_j⟩x_{j_1}\cdot x_{j_2}(2)$$
其中，$w\in R^d$和 $V_i\in R^k(k是给定的{)}^2$。加法单元$(⟨w,x⟩)$反应1阶特征的重要性，内积单元反映二阶特征的交互效应。

Deep部分是学习高阶特征交互的前向传播的神经网络。如图3所示，特征向量直接作为神经网络的输入 。图像和音频的处理输入的数据是连续和稠密的，而CTR的输入不同，它们需要对网络结构进行重新的设计。特别地，CTR原始的输入数据是稀疏的，高维的，类别变量和数值变量混合在一起。这表明，在输入到隐藏层之前，embedding层需要将输入向量压缩成低维稠密向量，以避免过拟合。

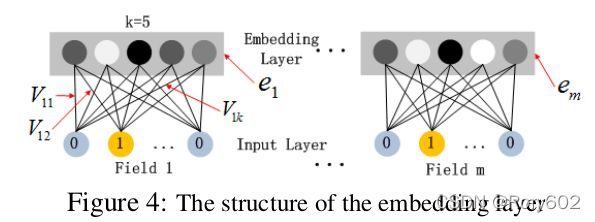
Figuire4展示来自输入层到embedding层的子网络结构。我们需要指出该网络结构有意思的两点。1）输入特征向量的维度是不同的，但是，他们的embedding的大小都是相同（$k$）。2）作为一种网络权重的FM模型隐向量（$V$）是通过压缩输入向量到embedding向量生成的。在有关于$V$的处理过程中，有些人是通过FM模型预训练$V$,我们没有那么做，我们将FM模型作为全局学习的一部分，此外还有DNN。embedding层的输出如下：
$$a^{(0)}=\left[e_1,e_2,\dots ,e_m\right](3)$$
$e_i$是embedding第$i$个filed，m是field的数量。然后，$a^{(0)}$是神经网络的输入，前向传播过程如下：
$$a^{(l+1)}=\sigma \left(W^{(l)}{a}^{(l)}+b^{(l)}\right)(4)$$
其中，$l$是层的深度，$\sigma$是激活函数。$a^{(l)}，W^{(l)},b^{(l)}$分别是输出、模型的权重、$l$层的常熟项。然后，产生稠密的实数特征向量。作为sigmoid函数的输入，进行CTR预测：$y_{DNN}=\sigma \left(W^{|H|+1}\cdot a^H+b^{|H|+1}\right)$,其中，$|H|$是隐藏层的层数。

需要重点指出的是FM和DNN共享特征的embedding层，这样有两个好处：1）同时能够学习低阶和高阶的特征交互。2）不像Wide&Deep需要特征工程，DeepFM不需要进行特征工程。

3.2和其他神经网络模型的对比

本节对DeepFM和现存的其他用于CTR预测的深度模型进行对比。

FNN模型：FNN是通过FM模型初始化的神经网络模型。通过FM进行预训练存在两方面的限制：1）embedding层的参数受FM模型的影响。2）FM模型预训练的引入，导致模型的效率降低。除此之外，FNN只能捕捉高阶的特征交互。

PNN:为了捕捉高阶特征的交互，PNN在embedding层和第一个隐藏层之间引入乘积层。根据乘积方式的不同，PNN存在以下3种情况：IPNN.OPNN和PNN*，其中，IPNN是基于向量的内积。OPNN是外积，PNN*是兼顾内积和外积。

为了使计算更加高效，作者对内积个外积计算采用近似的方式：1）内积计算随机删除一些神经元。2）外积是将m个k维的特征向量压缩成1个k维的向量。由于压缩会 导致很多信息丢失，所以我们认为，这种结果是不稳定的。尽管内积更加值得信赖，但是，计算复杂度较高，因为乘积层的输出需要连接隐藏层所有的输出。和PNN相比，DeepFM直接连接最后一层输出（只有一个神经元），像FNN一样，所有的PNNs忽略低阶特征交互。

这个模型利用 FM代替LR，这个操作类似DeepFM，DeepFM共享FM和Deep之间的Embedding层。Embedding共享机制通过低阶和高阶特征交互影响特征表示。

总结：DeepFM和其他深度模型的对比如下图所示：

4.实验

4.1实验设置

数据集：

1)Criteo Dataset: 包括4500万用户的点击记录。其中13个连续变量，26个类别变量。将数据集按照9:1进行划分，90%用于训练，10%用于测试。

2)Company Dataset: 为了验证DeepFM在工业化CTR预估中表现，我们使用Company*dataset。我们收集来自Company* APP Store中连续7天用户点击数据用于训练。下一天的数据作为测试。整个过程大约有10条数据，在这个数据集中 ，有app特征数据（唯一标示，类别）、user的特征数据（用户是否下载app）、上下文特征（操作的时间）。

评估方式

使用auc和logloss（交叉熵）

模型比较

我们对9个模型进行实验：LR、FM、FNN、PNN(3种情况)、Wide&Deep(wide部分包括LR和FM)和DeepFM。Wide&Deep将这两种情况分别命名为LR&DNN和FM&DNN。

参数设置

FNN&PNN: (1) dropout:0.5 (2) 网络结构：400-400-400；（3）优化器：Adam （4）激活函数：IPNN采用tanh，其他深度模型采用relu。为了公平起见，DeepFM采用同样的设置。LR和FM分别采用FTRL和Adam优化器，FM隐向量的维度是10.

4.2效果评估

效率评估
$$评估公式=\begin{array}{c}\text{ ltraining time of deep }CTR\text{ model }\\ \text{ |training time of }LR|\end{array}$$
Figure 6左侧是cpu训练，右侧是GPU训练 ，结论如下：

• FNN的预训练导致模型整体效率降低。
• 尽管在GPU上IPNN和PNN*训练的效率有了显著的提升，由于内积操作的原因，计算过程复杂度仍然较高。
• DeepFM在效率方面获得较好的表现。

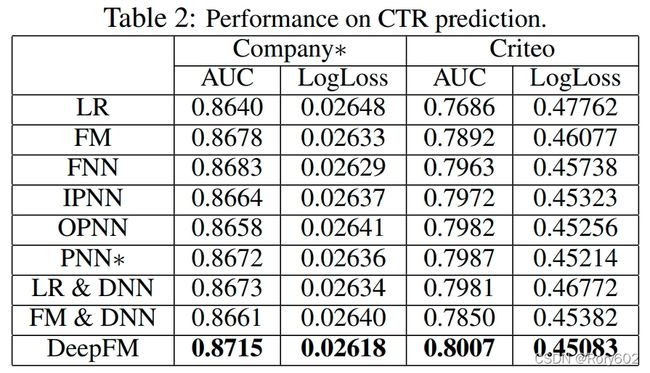
效果对比

• 特征交互会提高CTR模型的预估的效果。未采用特征交互的LR模型效果比其他模型效果差。
• 同时学习高阶和低阶交互特征的DeepFM比只采用低阶交互的FM或者高阶特征交互的（FNN,IPNN,OPNN,PNN*）模型效果好。
• 共享特征embedding层相对于采用分离式embedding层的（LR&DNN和FM&DNN）效果好。

4.3超参数研究

基于Company*dataset，调研以下参数对模型修过的影响：1）激活函数；2）drop rate ;3)每层网络神经元的个数；4）隐含层个数；5）网络的形状

激活函数

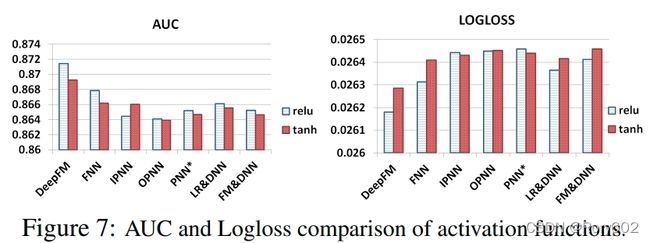
relu和tanh比sigmoid更适合深度模型。在本文中，我们比较relu和tanh的模型效果。如Figure 7所示，relu比tanh更适合深度模型，IPNN除外。可能原因：relu会导致数据的稀疏性。

Dropout

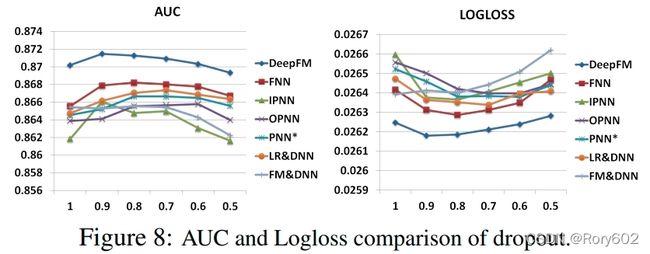
Dropout对模型的精度和复杂性进行折中的方法。我们设置dropout为1.0.0.9,0.8，0.7,0.6,0.5。如Figure8所示，当设置合适的dropout，模型会达到最好的效果。

每层网络神经元的个数

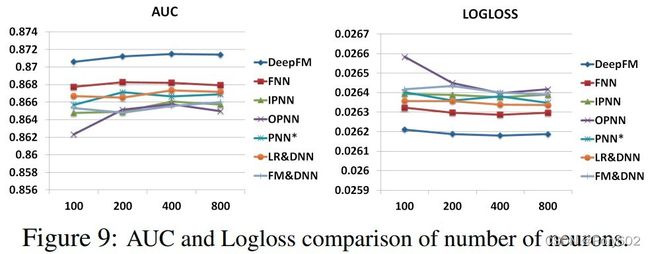
当其他影响因素保持不变时，增加每层网络神经元的个数会增加模型的复杂性。从Figure 9中发现，增加神经元的个数不能总是带来效果的提升。举例来说，当神经元的个数从400增加到800时，DeepFM模型整体表现比较稳定，OPNN甚至表现出模型效果下降。这是因为过于复杂的模型容易导致过拟合，在本数据集中，200或者400是比较不错的选择。

隐藏层的个数

如Figure10所示，随着隐藏层个数的增加，模型效果开始提升，增加到一定的程度，模型效果开始下降。这也是过拟合的原因导致。

网络结构

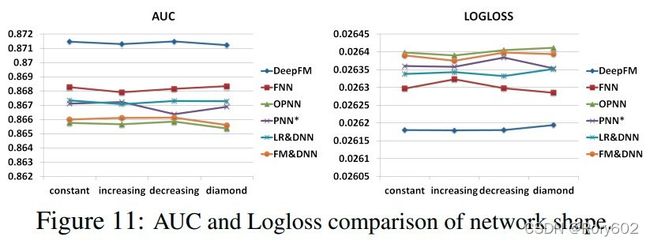
我们尝试测试不同的网络结构：常数型、增加型、下降型、锥形型。当我们改变网络结构时，我们固定隐含层的个数和神经元的总数。例如，我们的隐含层是3，总体神经元个数是600，四种不同的网络结构分别是：常数型（200-200-200），增加型(100-200-300),下降型(300-200-100）,锥形型(150-300-150)。如Figure 11所示，常数型的网络结构比其他三种效果要好。

5.结论

DeepFM克服现存模型的不足，具有良好的模型效果。主要的优势有以下几点：1）不需要进行预训练；2）学习到高阶和低阶的特征交互；3）引入特征embedding，避免特征工程。在实际数据集应用中，获得良好的效果，主要体现以下两点：1）根据auc和logloss评估，效果最好。2）通过和其他模型的对比，效率最高。