字典树基础与应用

字典树（Trie)

字典树（Trie）也叫前缀树，是一种针对字符串进行维护的树。

• 其中的键通常是字符串，由节点在树中的位置决定，键保存在边而不是在节点

• 一个节点的所有子孙具有相同的前缀，也就是这个节点代表的字符串，根节点代表空字符串

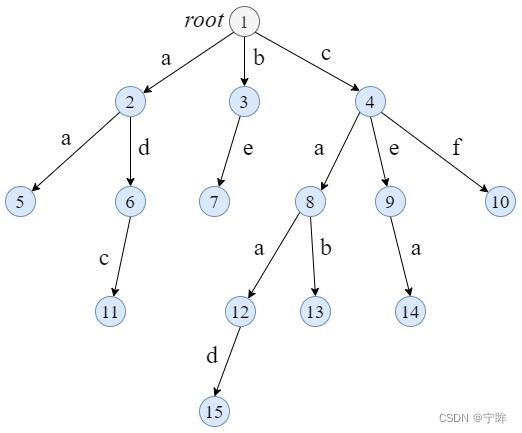
下图中，1 - 4 - 8 - 13有3条边，表示字符串cab

初始化根节点

• 假设字典中只有26个小写字母，则每个节点至多有26个子节点
• is_end表示当前字符串是否在这里截止，False代表前缀，True代表末尾

class Trie:

    def __init__(self):
        self.children = [None] * 26
        self.is_end = False

插入字符串

从字典树的根开始，向下查找字符串的插入位置，对于当前字符对应的子节点，有两种情况：

• 子节点存在，node = node.children[ch]，向下查找子节点
• 子节点不存在，创建一个新的节点，放在当前字符对应的位置上，再向下查找子节点
• 遍历完字符串word，也就是到了word对应的最后一个节点，打上标记node.is_end = True

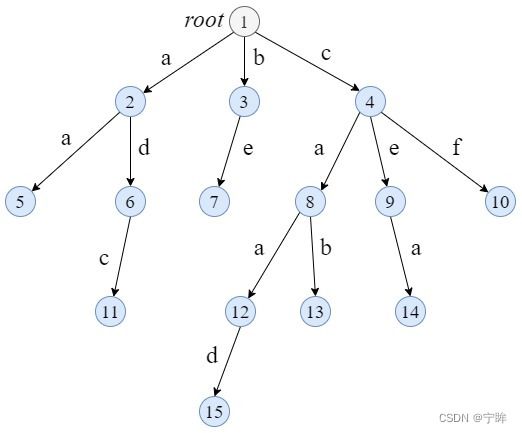
比如说在下面的字典树中插入字符串cat，

查找第一个字符c存在，继续向下，a也存在，继续向下，t不存在

于是在a的子节点下面，创建一个新节点t，至此，cat字符串就被插入到了字典树中

    def insert(self, word: str) -> None:
        node = self
        for ch in word:
            ch = ord(ch) - ord('a')
            if not node.children[ch]:
                node.children[ch] = Trie()
            node = node.children[ch]
        node.is_end = True

查询字符串

从字典树的根开始，向下查找字符串，对于当前字符对应的子节点，有两种情况：

• 子节点存在，node = node.children[ch]，向下查找子节点
• 子节点不存在，说明字典树中没有该前缀，返回None
• 根据前缀查找结果，判断最后节点是否是末尾节点，如果是，说明找到了该字符串；如果不是末尾节点，说明只找到了该字符串的前缀

    def searchPrefix(self, prefix: str) -> "Trie":
        node = self
        for ch in prefix:
            ch = ord(ch) - ord('a')
            if not node.children[ch]:
                return None
            node = node.children[ch]
        return node


    def search(self, word: str) -> bool:
        node = self.searchPrefix(word)
        return node is not None and node.is_end


    def startsWith(self, prefix: str) -> bool:
        node = self.searchPrefix(prefix)
        return node is not None

---

完整代码

对应Leetcode上的题目：208. 实现 Trie (前缀树) - 力扣（Leetcode）

class Trie:

    def __init__(self):
        self.children = [None] * 26
        self.is_end = False


    def insert(self, word: str) -> None:
        node = self
        for ch in word:
            ch = ord(ch) - ord('a')
            if not node.children[ch]:
                node.children[ch] = Trie()
            node = node.children[ch]
        node.is_end = True
    
    
    def searchPrefix(self, prefix: str) -> "Trie":
        node = self
        for ch in prefix:
            ch = ord(ch) - ord('a')
            if not node.children[ch]:
                return None
            node = node.children[ch]
        return node


    def search(self, word: str) -> bool:
        node = self.searchPrefix(word)
        return node is not None and node.is_end


    def startsWith(self, prefix: str) -> bool:
        node = self.searchPrefix(prefix)
        return node is not None

字典树的应用

1803. 统计异或值在范围内的数对有多少 - 力扣（Leetcode）

给你一个整数数组 nums （下标 从 0 开始 计数）以及两个整数：low 和 high ，请返回 漂亮数对 的数目。

漂亮数对 是一个形如 (i, j) 的数对，其中 0 <= i < j < nums.length 且 low <= (nums[i] XOR nums[j]) <= high 。

• $1<=nums.length<=2\ast 10^4$
• $1<=nums[i]<=2\ast 10^4$
• $1<=low<=high<=2\ast 10^4$

---

题目求解异或结果在 [low, high]之间的数对个数，可以转换为求解异或结果在(0, high]和(0, low)的个数之差

用$f(x)$表示数组中异或结果小于x的数对个数，问题转换为求解$f(high+1)-f(low)$

看到这题第一个想到的是暴力遍历nums，两两取异或，根据异或结果计数，这是我第一次写的代码，毫无疑问超时了

class Solution:
    def countPairs(self, nums: List[int], low: int, high: int) -> int:
        n = len(nums)
        ans = 0
        for i in range(n-1):
            for j in range(i+1, n):
                if low <= nums[i] ^ nums[j] <= high:
                    ans += 1
        return ans

怎么在这题使用字典树呢？

自己用笔写一下，我们比较nums[i]^nums[j]与x的结果时，怎么比较最快？答案是将nums[i]、nums[j]和x都转换为二进制，为了表示方便，将nums[i],nums[j],x写作a,b,c，分别转为二进制数$a_i{a}_{i-1}...a_2{a}_1，b_i{b}_{i-1}...b_2{b}_1，c_i{c}_{i-1}...c_2{c}_1$，我们从高位往低位比较，当找到一个$j(j<=i)$，满足$a_j$^$b_j$<$c_j$时，就不会继续往下比较了，因为不管后面是什么结果，a异或b的结果都会比c小。

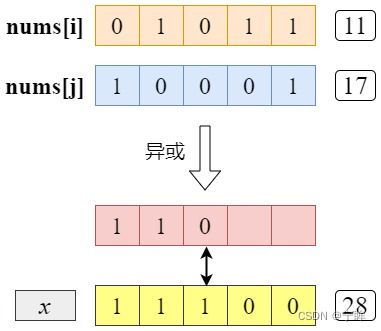
上面讲的比较抽象，下面用画图举例说明，nums[i]=11，nums[j]=17，x=28

从左往右比较，当比较到第3位时，异或结果是比x小的，所以后面就不用比较了。

鉴于这一特性，我们可以把nums转为前缀表（字典树），将nums中的元素看作二进制表示的字符串

• 字符串只包含0和1
• 由于$1<=nums[i]<=2\ast 10^4$，而$2\ast 10^4<2^{15}$，因此字符串的长度是15（高位补零就好）

初始化

每个节点除了包含两个子节点外，还有一个cnt属性，表示根结点到该节点路径为前缀的字符串个数。

class Trie:
    def __init__(self):
        self.children = [None] * 2
        self.cnt = 0

插入字符串

从字典树的根开始，向下查找字符串的插入位置，对于当前字符对应的子节点，有两种情况：

• 子节点存在，node = node.children[ch]，向下查找子节点
• 子节点不存在，创建一个新的节点，放在当前字符对应的位置上，再向下查找子节点

每遍历一个节点，不管节点是否存在，节点的cnt都要加1

    def insert(self, word):
        node = self
        for i in range(15, -1, -1):
            # 从高位取数字
            flag = word >> i & 1
            if not node.children[flag]:
                node.children[flag] = Trie()
            node = node.children[flag]
            node.cnt += 1

查询字符串

从字典树的根开始遍历，向下查找字符串的插入位置，并记录满足条件的前缀数量

• 子节点不存在，说明字符串这条路径到了末尾，返回累加的前缀数量
• x是基准值，子节点存在时有两种情况：
  • 如果x的当前位为1，就加上异或结果为0的子节点的前缀数量（小于），然后走向异或结果为1的子节点node = node.children[flag ^ 1]
  • 如果x的当前位为0，就要走向异或结果为0的子节点node = node.children[flag]
  • 注意，flag ^ 1 ^ flag = 1，flag ^ flag=0

比如在下面的字典树中查询17的异或结果，基准值为28，答案为5

    def search(self, a, x):
        node = self
        ans = 0
        for i in range(15, -1, -1):
            if not node:
                return ans
            # 基准数x的第i位数字
            y = x >> i & 1
            # 查询数a的第i位数字
            flag = a >> i & 1
            if y == 1:
                # 只有当异或结果可能为0时，才记录cnt
                if node.children[flag]:
                    ans += node.children[flag].cnt
                node = node.children[flag ^ 1]
            else:
                node = node.children[flag]
        return ans

---

为防止重复比较，将nums中的元素依次放入字典树，每查询一个，放入一个。

class Solution:
    def countPairs(self, nums: List[int], low: int, high: int) -> int:
        ans = 0
        tree = Trie()
        for x in nums:
            ans += tree.search(x, high + 1) - tree.search(x, low)
            tree.insert(x)
        return ans

完整代码：

class Trie:
    def __init__(self):
        self.children = [None] * 2
        self.cnt = 0

    def insert(self, word):
        node = self
        for i in range(15, -1, -1):
            flag = word >> i & 1
            if not node.children[flag]:
                node.children[flag] = Trie()
            node = node.children[flag]
            node.cnt += 1

    def search(self, a, x):
        node = self
        ans = 0
        for i in range(15, -1, -1):
            if not node:
                return ans
            # 基准数x的第i位数字
            y = x >> i & 1
            # 查询数a的第i位数字
            flag = a >> i & 1
            if y == 1:
                # 只有当异或结果可能为0时，才记录cnt
                if node.children[flag]:
                    ans += node.children[flag].cnt
                node = node.children[flag ^ 1]
            else:
                node = node.children[flag]
        return ans


class Solution:
    def countPairs(self, nums: List[int], low: int, high: int) -> int:
        ans = 0
        tree = Trie()
        for x in nums:
            ans += tree.search(x, high + 1) - tree.search(x, low)
            tree.insert(x)
        return ans