Scikit-Learn实现线性回归数据分析

目录

1、使用pandas来读取数据

2、生成X，y数据

3、划分训练集和测试集

4、运行Scikit-Learn的线性模型

5、对模型进行评价

6、交叉验证

7、画图观察真实值与预测值的变化关系

---

数据源是单车共享数据，前期已经实现了特征工程(数据的预处理),所以可以直接拿来使用。

1、使用pandas来读取数据

from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
from sklearn import linear_model
#pd.set_option('display.max_colwidth',1000)
#导入特征工程处理之后的数据
data=pd.read_csv('FE_bikesharing_train.csv')
print(data.shape)

如果出现：

    

则表示数据读入成功，一共有731个样本，每个样本有35列

2、生成X，y数据

y=data['cnt']
X=data.drop('cnt',axis=1)
#print(X)

3、划分训练集和测试集

把X和y的样本组合分成两部分：训练集和测试集

#数据的分割 80%用于训练 20%用于测试
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=42)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

如何查看训练集的维度：

    

可以看到80%的数据用来作为训练，20%的数据用来测试，表示数据分割成功。

4、运行Scikit-Learn的线性模型

Scikit-Learn的线性回归算法的原理的最小二乘法（OLS）

lm=linear_model.LinearRegression()
lm.fit(X_train,y_train)
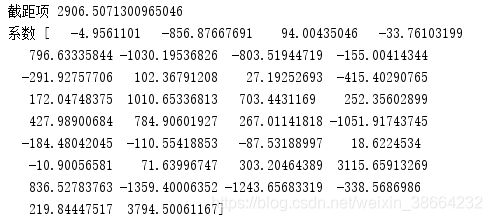
print('截距项',lm.intercept_)
print('系数',lm.coef_)

截距项跟各个系数为：

    

5、对模型进行评价

对线性回归模型，常用的评价方案是均方差（Mean Square error,MSE）或均方根差(Rooted Mean Squared Error,RMSE)

代码实现：
 

#模型评价,模型拟合测试集
y_pred=lm.predict(X_test)
from sklearn import metrics
#用scikit-learn计算MSE
mse=metrics.mean_squared_error(y_test,y_pred)
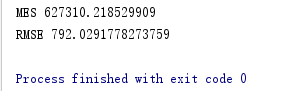
print('MES',mse)
#计算RMSE
rmse=np.sqrt(metrics.mean_squared_error(y_test,y_pred))
print('RMSE',rmse)

输出：

    

6、交叉验证

可以通过交叉验证持续优化模型，采用10折交叉验证（cv=10）

注意：这里的estimator是线性模型（也有可能是Ride、Lasso等模型）

from sklearn.model_selection import cross_val_predict
predicted=cross_val_predict(lm,X,y,cv=10)
cross_mse=metrics.mean_squared_error(y,predicted)
cross_rmse=np.sqrt(metrics.mean_squared_error(y,predicted))
print('CROSS_MSE',cross_mse)
print('CROSS_RMSE',cross_rmse)

输出：

    

对比一下5中的MSE和RMSE发现均比它们大，这是因为K折的数据是全体数据，而5中仅仅是对20%的数据做的测试。

7、画图观察真实值与预测值的变化关系

fig,ax=plt.subplots()
ax.scatter(y,predicted)
ax.plot([y.min(),y.max()],[y.min(),y.max()],'k--',lw=4)
ax.set_xlabel("Measured")
ax.set_ylabel('Predicted')
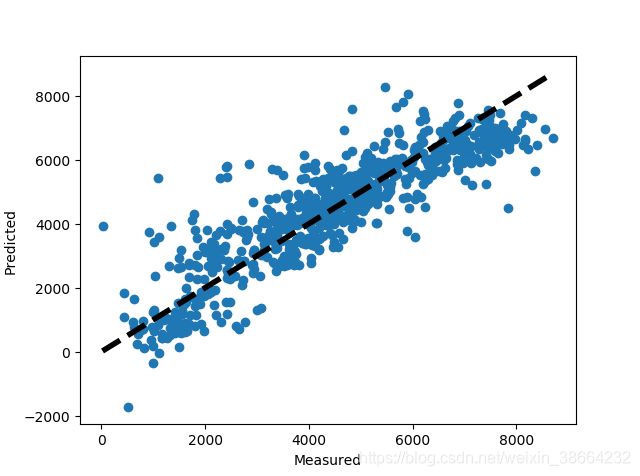
plt.show()

图：

    

对于越接近y=x的直线上的点代表预测损失越小。