Tutorial: The Hawkes Processes

Tutorial: The Hawkes Processes

---

前言

在这里，我们对The Hawkes process背后的思想和理论做一个非正式的介绍。我们假设读者对统计学和机器学习有一定的了解。然而，我们并不是让读者通过繁重的数学理论去学习，而是试图强调霍克斯的思想及其潜在的应用领域。

1.Background

对机器学习和其他学科来说，有趣的自然现象包括时间作为分析的中心维度。那么，一项关键任务就是捕捉和理解时间线上的统计关系。处理时态数据的主力模型是在时间序列分析下收集的。这类模型通常将时间划分为大小相等的桶，并将数量与模型操作的每个桶相关联。这就是离散时间形式主义，出现在许多机器学习中常见的模型中，比如卡尔曼滤波器和隐马尔可夫模型，正如计量经济学和预测学中常见的模型，如ARIMA或指数平滑法。
假设我们获得了金融市场中所有“价格跳跃”的时间戳，从时间的角度来探索这些数据集，我们通常采取“在统一的时间网格上聚合统计数据，并在这些聚合上运行模型”的方式。
具体来说，以“金融市场价格事件的毫秒时间戳：

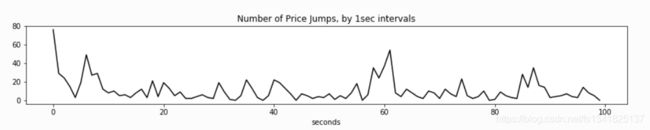
选择离散时间模型有很多原因。首先，数据可能只能由一个真实世界的观察者（系统）在统一的时间网格中收集，而没有更多的细粒度数据可用。当然，再复杂的模型也没什么用。第二，这些模型可能足以解释时间关系。

然而，许多真实世界的数据都带有时间戳。也就是说，它们对应于连续时间内的离散事件。因此，分析员的工作是更好地解释粒度时间关系，并回答诸如“下一个事件何时发生？”或“我们预计在接下来的5分钟内会发生多少事件”之类的问题。通过基于连续时间（事件可以在任何时间发生）和离散事件（事件发生是瞬时的）的形式主义的分析，这些问题的答案被解开了。此外，分析的框架不依赖于数据的任意离散化，这很可能导致有价值信息的丢失。

例如：绘制事件本身，这更直观。图中的每个“点”都是唯一的数据点，任意时间的“网格”都会导致信息的丢失。

2.Temporal Point Processes

1）.引入定义

Stochastic processes(随机过程)被定义为collections of random variables随机变量的集合。
我们还将为这个集合配备一个索引集。例如，为上面的“离散时间”数据形式化一个模型

这里Xt组成集合，而Z+是索引集
特定的依赖性（或者更确切地说，独立性）结构和{Xt}之间关系的其他参数假设决定了随机过程。请注意，随机变量或过程的实现是由所有Xt（通常是我们观察到的部分）所取的值确定的整个轨迹。

2）.时间点过程

当索引集是R时，事情会稍微有趣一些。再次将索引集解释为时间，我们就得到了连续时间过程。该过程的每个实现现在完全决定了域R上的一个函数。在机器学习中，高斯过程就是这样一个例子。另一个例子是维纳过程（布朗运动），它是定量金融学的一个重要分支。

从高斯和维纳过程（上面的一个程式化例子）中提取实现，我们得到函数f:R→R。为了我们对离散事件建模的目的，让我们将这一系列可能的函数限制为R上定义的一类特殊的阶跃函数。也就是说，我们将处理函数N:R+→Z+，这是阶跃函数，使得s>t意味着N（s）≥N（t）。我们称这种过程为计数过程。

这是定义时间点过程的一种方法，即概率分布，使得每次绘制都是实线（通常是“时间线”）上的点的集合。每个“点”将对应于我们上面例子中的一个“事件发生”，我们将使用这些理论设备来探索“事件发生”是如何随时间分散的。

3.Poisson Process

我们从最简单的时间点过程泊松过程开始。泊松过程被描述为最简单的过程，完全随机性的过程[1]，或者RobertGallager将其描述为“我们希望实现的一切都是真实的过程”。

泊松过程具有完全独立性。除了点过程简单（没有两点重合）外，Poisson过程的定义性质如下任意两个不相交区间上的出现次数是独立的Poisson过程的定义中经常给出以下性质。令人惊讶的是，这个属性实际上是上述属性（以及其他一些更技术性的假设）的结果

这里我们让N（A）表示区间A上的点数，当然，它本身就是一个随机变量。Po表示泊松分布。ξ 有点棘手。它是R上的一个测度，因此它取非负值，满足ξ(∅)=不相交集的测度之和等于不相交集的并集的测度。然而

我们定义函数λ, 强度函数。对于那些熟悉概率论的人来说，它应该类似于密度函数。一种思考的方式是λ(t） 定义（在极限）在时间t之后在无穷小间隔内发生的概率。所以越高λ(t） ，在t内及其周围观测点的概率越高（假设λ(t） 是光滑和美好的）。最后让我们注意到，由于我们对简单性的假设，上面的等式是可能的——没有两点可以落在这个无穷小的区间上。


上面的蓝线表示强度函数λ(t） ，而每一行黑点都是泊松过程的结果。注意这些点在强度函数的“峰值”附近有更高的倾向。

尽管如此，圆点的出现是完全独立的。非正式地，给定λ(t） ，每个事件独立发生，不受其附近是否有其他事件的影响。

泊松过程的一个重要特例是当强度函数为常数时，即。λ(（吨）=μ. 我们称这种特殊情况为齐次Poisson过程，并进一步刻画了平稳性。非正式地说，一个点出现在t附近的概率是恒定的，这使得点出现在时间轴上任何地方的可能性相等。具体来说，这个过程中的样本看起来像λ(t） =3）：

泊松过程是许多应用的基础，例如排队论。然而，在那里，到达队列中的人或包可以合理地被期望服从独立性。然而，在许多其他应用程序中，独立性假设不能满足对域的基本直觉。例如，众所周知，重大金融事件会吸引（激发）其他人的兴趣。地震不仅随机发生，而且随机触发其他地震。在这些领域，我们理解，泊松过程导致了过度简化。我们必须用更具表现力的一类模型来工作。

4. Self-exciting Processes

到目前为止，我们使用实线来定义点过程，只是相当随意地表示时间。同一组R可以用来表示断层线上的距离，例如深度；当对地震进行“横截面”分析时。在这里，我们将开始赋予时间一些意义。

我们正在寻找打破独立性假设的方法，以某种方式让事件的发生依赖于其他事件。一个很自然的方法是让“未来”（真实路线的其余部分被认为没有被观察到）依赖于过去。具体来说，在R上，我们将λ(t） 取决于[0，t]中的出现次数。
在泊松过程中，强度函数λ(t） 是确定性的。这里，让我们来介绍一下λ∗(t） ，条件强度函数。λ∗(t） 确定一个点在t之后的无穷小间隔内发生的概率，给定在t之前发生的事件（星号将作为此条件的提醒）。实际上，λ∗(t） 是t的函数，以及出现次数{ti | ti

我们在这里不谈细节，但这是时间点过程的一般理论[1]的一个基本结果λ∗(t） ，在一组温和的条件下，这将导致一个定义良好的点过程。此外，这样的描述将使可能性的计算变得简单，并且是可解释的。详见[1]第7章。
如上所述的过程被称为进化、自我调节或条件强度点过程[1]、[2]。如果一个点的出现只会增加未来λ∗(t） ，另一个术语更合适：自我激励。

5.Hawkes Processes

霍克斯过程[3]通常是进化过程的第一个也是最流行的例子。（单变量）Hawkes过程由条件强度函数定义

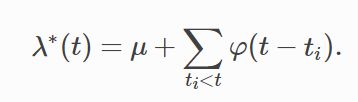
让我们花点时间把这个等式分解一下。在任意时刻t，条件强度函数至少为μ>0，背景强度。然而，它也线性地依赖于时间t之前发生的事件的影响。也就是说，这种依赖是通过一个触发核函数实现的φ(.), 延迟t的函数−当前时间和上一个事件的时间戳之间的ti。请注意φ 是非负的(φ(十）≥0,∀十≥0和因果关系φ(x） =0，∀x<0。它通常是单调递减函数（如指数衰减或幂律衰减）。
最常用的核函数是指数衰减φ(十）=αβ经验(−βx） 是的。注意，这个分解形式∫β经验(−βx） =1，便于解释。α>0被称为传染性因子，它定义了由任何给定事件激发的新事件的平均数目。β经验(−βx） 另一方面，是简单的指数密度函数，它控制着相互激励的事件之间延迟的概率分布。这就是为什么它也被称为延迟密度。

到目前为止，我们讨论了“单变量”霍克斯过程。然而，我们可以假设，每个事件的发生都有一个来自有限集合的离散标记或标签。具体地说，回到我们的财务示例，事件发生可以属于不同的类型或资产。在这种情况下，人们不仅可以将系统视为一个单一的随机过程，而且可以将其视为一系列相互作用或相互激励的时间点过程。
假设观察到的数据现在是一组有序对{（ti，ci）}，其中ti∈R+是时间戳，ci∈{0,1，…，K}是给定事件所属进程的标识符。我们用一组条件强度函数形式化了一个多元Hawkes过程


其中，现在A被解释为传染性矩阵，而Al，k被解释为将由l型事件引起的进一步k型事件的预期数量。

在Hawkes过程的背景下，似然计算、参数估计和推理问题并不简单，但它们已经超出了本文的范围。参见[4]，[5]了解更严格处理霍克斯过程的广泛调查。此库中的大多数实现及其相应的API文档都引用了这些工作中列出的标准术语。

霍克斯过程

不同于非时齐的泊松（Possion）过程的强度函数λ \lambdaλ(t)是个确定的函数，存在计数过程在时刻t强度函数{N(t),t>=0}的值，记为，它是个随机变量，其值依赖于直至时刻t的过程的历史。也就是说，若将直至时刻t的过程的历史记为ψ \psiψt，则在时刻t的强度率是一个随机变量，其值由所确定，且使

hawkes过程是具有随机强度函数的计数过程的例子之一。这种计数过程假定了存在一个基本的强度值λ \lambdaλ>0，且对每个事件附以一个称为标志值的非负的随机变量，其值独立于以前发生的一切事件，且具有分布F。假定每当一个事件发生时，随机强度函数的当前值就增加了这个事件的标志值得量，且这个增加的量以指数速率按时间递减。更确切地，若到时刻t为止，已发生事件的总数为N(t)，事件的发生时间S1

换句话说，hawkes过程是满足如下条件的计数过程：
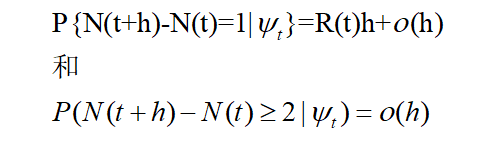
1.R(0)=λ \lambdaλ;
2.每当一个事件发生时，过程的随机强度增加一个等于此事件的标准值得量；

3.若在s和s+t之间没有事件发生，则
因为每当一个事件发生时强度增加，所以称hawkes过程为自激过程。
下面介绍两条引理：
1.满足N(0)=0的计数过程N(t)，其随机强度函数为R(t)，记m(t)=E[N(t)]，则

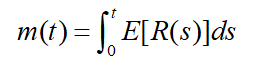
2.若在hawkes过程中标志值的均值为μ \muμ，则对此过程有

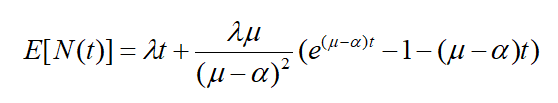
思想

很久以前，这个hawkes教授首先做了这件事，他提出了hawkes process ：
他假设过去的事件 对未来事件 都有一个短暂的正向影响，
也就是过去的事件 会 正向提高 未来事件发生的概率 ，
基于这个假设， 他把intensity function 定义为一个 base level + 过去每一个事件对后面的事件带来的影响的加和，
这个影响是不同事件之间的相互影响，有k个事件，就有k的平方个阿尔法 ， 这个正向的影响随着 事件衰减，所以要加上 后面这个指数项
也就是说 hawkes process假设每一类别事件他的intensity function在一个base level的基础上不断被过去事件激发，激发又随着事件消减

time LSTM

作者提出了一个continuous-time LSTM
先看右边的公式：正如刚才所说的，可以把intensity function 作为一个连续时间上变化的hidden state上的non-linear function 。由于我们知道 hidden state 是被update 和 cell memory 共同决定
我们假设 cell memory 是随着时间变化的 ，从而使得H也随着时间变化
通常在普通的lstm中gate encode cell memory C 的变化， 在新模型中有两个C
一个表示暂态的memory 就是这个C ， 他表示第i 次事件发生的时候，他变成了Ci+1
同时类似的，我们还可以有另外一个cell memeory 表示一个稳态的memory Cbar
他表示在稳态的时候cellmemory处于什么样的值，我们可以假设在每次事件发生之后和下一次事件发生之前，真正的cell memory T 会从暂态cell memory 开始 逐渐的向 稳态C bar变化，变化率 由一个可以被学习到的 daita function 决定
这样的话 由于c的每一个 element都是对着时间指数变化的 这堆element做一个combination 和一个non-linear 的变换，理论上可模拟 任何方式变化的时间函数 ， 也就是说当我们把很多指数变化的函数组合起来的时候，我们可以让他们的组合 来逼近任何复杂形状的函数，那我们就可以得到任何复杂
形状的intensity function
举个例子 ，就是左边这张图，下面的黄线代表cell memory，假设用的是有3个hidden node 的LSTM
也就是他的维度D=3，每一个维度都随着事件递增或递减，当下一个维度发生之后，这个cell memory都会发生显著的变化，事件发生之后，cell memory 会发生显著变化，以一定速率递增或者递减
假设有两个不同事件，绿色和粉色事件，每一个事件都有它的 intensity function，他俩都可以以一些参数被写成这三个cell，c1,c2,c3的non-linear projection,那么我们可以看到 随着横轴时间轴的推移，cell memory 不断产生变化 ， intensity function 也不断产生变化 ， 当粉色事件发生，粉色事件作为输入，改变了cell memory的值 ，进而改变了 intensity function的值 ， 新一轮的缓慢变化又开始了
整个这部分内容就是 neural hawkes 的核心内容 ，作者用连续时间上的LSTM 来capture连续时间
上hidden state的变化 ，进而能把intensity function 表示成 hidden state的一个复杂的non-linear projection。从未capture到各种复杂的影响

总结

今天是一个无情的复制粘贴翻译侠客