矩阵乘法复杂度分析

一 背景

在很多机器学习或者数据挖掘论文中，里面或多或少的涉及到算法复杂度分析。进一步思考，是如何得到的呢？

很长时间里，我也感受到比较疑惑，阅读论文过程中，在涉及到这部分内容时，会直接跳过算法复杂度分析这快。

其一是因为比较烧脑。虽然知道复杂度分析是对算法总体上的概况，用来进行算法间好坏的比较（由此可见，重要性）。

其二是算法分析基础比较薄弱（个人主观上也是不想的）。

算法复杂度在《数据结构》课程中也或多或少的涉猎，说完全不知道属于自己骗自己，简单的一些例子还是会分析的，但当涉及到复杂的目标方程是，特别是含矩阵运算，就不知道如何分析了。也没有领路人，不知道如何下手。随着看的论文数量上升，慢慢摸索过程中突然就通了，知道如何去分析了。写这篇博客的目的希望读者能够明白如何对矩阵乘法进行复杂度分析，少走一些弯路。笔者先介绍2个矩阵相乘复杂度，然后介绍3个矩阵相乘复杂度，最后介绍几篇论文里面的loss方程，如何运用矩阵乘法复杂度去分析算法的好坏。

需要的基础，初步了解《数据结构》第一章知识，至少知道算法复杂度是什么以及如何表示。

二  矩阵乘法

对于矩阵A(n*m),B(m*n), 这里A(n*m)表示A是n行乘m列的矩阵。

如果A*B，那么复杂度为O(n*m*n),即O(n^2m) 。进一步思考，为什么呢，直接代码解释：

 for(i=0;i

一个for循环是O(n),这里是三个for循环，所以为O(n*m*n)。（ps：个人感觉还是看代码比较好理解，后面三个矩阵乘法时，就会更加体会到）

二  三个矩阵乘法

对于矩阵A(m*n),B(n*m)和C(m*n),            这里A(m*n)表示A是m行乘n列的矩阵。(PS:这里记号和前面不同，主要方便和知乎截图符号一致)

• A*B，那么复杂度为O(m*n*m),即O(m^2n) 。
• D(m*m)=A*B运算完后在和C运算。
• D*C,那么复杂度为O(m*m*n),即O(m^2n) 。

与(A*B)*C等价。整个过程算法复杂度为O(m^2n) 。（一开始笔者以为是O(m^2n)*O(m^2n) = O(m^4n^2), 其实这样理解是错的，下面介绍）

这里与知乎这篇一致，截图如下：

为了方面理解，笔者直接上代码，这样清楚一点。

int A(m*n),
int B(n*m)
int C(m*n)

int D(m*m)
int E(m*n)

//先计算D=A*B
 for(i=0;i

同样的，一个for循环是O(n),这里的第一次三个for循环，矩阵乘法复杂度为O(m*n*m)=O(m^2n)。

第二次为O(m^2n)

但因为是顺序执行，所以总的复杂度是相加而不是相乘。

故为O(m^2n)+O(m^2n)

= O(2*m^2n)

= O(m^2n)，在算法分析过程中，系数可以忽略

上面写的是伪代码，随手敲的，思想理解到就行。

四 loss方程复杂度分析

论文1： Fast Attributed Multiplex Heterogeneous Network Embedding, CIKM,2020.  需要的可以自己下载。

目标方程截图如下：

算法复杂度为O(n^3*K  + n^2*m  + n*m*d),  计算方向从左到右。其中A(n*n), X(n*m)  ,R(m*d)， K为累加次数（相当于在外面加了一个for循环，遍历K次）

O(n^3*K)表示计算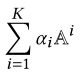，这里读者可能会比较懵，阅读原文会发现，这里的也是一个n*n的方阵，所以有n^3，在外面套一个for循环累加，就是K*n^3。

O(n^3*K  + n^2*m）表示计算

O(n^3*K  + n^2*m  + n*m*d)则表示全部过程。

作者后面做了计算优化，把算法负责度由O(n^3*K  + n^2*m  + n*m*d) 降到了O(K*e*n  + n*m*d)

O( n*m*d) 表示计算

O(K*e*n）表示计算