gtsam 学习十(ISAM2 理论)
翻译自:iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree
摘要
提出了一种新型的贝斯树处理稀疏矩阵,在转化为因子图,可以更好的求解平方根信息和映射问题。
文中提出了三个概念
- 使用概率密度项进行矩阵分解
- 介绍如何将矩阵分解转换为贝叶斯数和条件概率密度
- 基于贝叶斯树提供了一种新的系数非线性优化:ISAM2(进行重新排序和重新线性化,避免了批量更新)
问题描述
文章聚焦与如何用增量实时解决非线性问题,
-
利用增量即新的测量值实时更新估计值?:比如机器人的导航和规划
-
使用因子图求解一个状态估计文题
(1):定义一个因子图
F : 因 子 图 所 有 函 数 节 点 , f i ∈ F F:因子图所有函数节点,f_i\in F F:因子图所有函数节点,fi∈F
Θ : 因 子 图 所 有 因 子 节 点 θ j ∈ Θ \Theta:因子图所有因子节点\theta_j \in \Theta Θ:因子图所有因子节点θj∈Θ
E : 边 : 两 个 因 子 图 之 间 的 关 系 E:边:两个因子图之间的关系 E:边:两个因子图之间的关系
G : 一 个 因 子 图 G:一个因子图 G:一个因子图
G = ( F , Θ , E ) G=(F,\Theta,E) G=(F,Θ,E)
(2):由因子图可以得到因式分解为:
Θ i : 表 示 所 有 与 函 数 f i 相 邻 因 子 节 点 θ j 的 集 合 \Theta_i:表示所有与函数f_i相邻因子节点\theta_j的集合 Θi:表示所有与函数fi相邻因子节点θj的集合
e i j : 表 示 一 个 因 子 节 点 e i 与 一 个 函 数 节 点 e j 的 联 系 e_{ij}:表示一个因子节点e_i与一个函数节点e_j的联系 eij:表示一个因子节点ei与一个函数节点ej的联系
f ( Θ ) = Π i ( f i ( Θ i ) ) f(\Theta)=\Pi_i(f_i(\Theta_i)) f(Θ)=Πi(fi(Θi))
(3):得到目标函数为:
Θ ∗ = a r g m a x Θ f ( Θ ) \Theta^*=argmax_\Theta f(\Theta) Θ∗=argmaxΘf(Θ)
例如下图:
m : 路 标 测 量 值 m:路标测量值 m:路标测量值
c : 回 环 c:回环 c:回环
u : 里 程 计 u:里程计 u:里程计

-
假设测量模型为高斯模型
h i ( Θ i ) : 测 量 函 数 模 型 ( 理 论 值 ) h_i(\Theta_i):测量函数模型(理论值) hi(Θi):测量函数模型(理论值)
z i : 测 量 值 z_i:测量值 zi:测量值
∣ ∣ e ∣ ∣ ∑ 2 = e T ∑ − 1 e ||e||^2_{\sum}=e^T\sum^{-1}e ∣∣e∣∣∑2=eT∑−1e
f i ( Θ i ) = e − 1 2 ∣ ∣ h i ( Θ i ) − z i ∣ ∣ ∑ i 2 f_i(\Theta_i)=e^{-\frac{1}{2}||h_i(\Theta_i)-z_i||^2_{\sum_i}} fi(Θi)=e−21∣∣hi(Θi)−zi∣∣∑i2
目标函数更新为:
a r g m i n Θ ( − l o g f ( Θ ) ) = a r g m i n Θ 1 2 ∣ ∣ h i ( Θ i ) − z i ) ∣ ∣ ∑ i 2 argmin_\Theta (-logf(\Theta))=argmin_\Theta \frac{1}{2}||h_i(\Theta_i)-z_i)||^2_{\sum_i} argminΘ(−logf(Θ))=argminΘ21∣∣hi(Θi)−zi)∣∣∑i2
定义协防差矩阵为(马氏距离):
Σ : 协 防 差 矩 阵 Σ:协防差矩阵 Σ:协防差矩阵
∣ ∣ e ∣ ∣ Σ 2 = e T Σ − 1 e ||e||^2_Σ=e^T Σ^{-1}e ∣∣e∣∣Σ2=eTΣ−1e -
使用高斯牛顿/列文伯格方法求解非线性方程: h i ( Θ i ) h_i(\Theta_i) hi(Θi)
于是目标函数变为:
A : m × n 阶 的 雅 克 比 矩 阵 , m : 测 量 值 的 个 数 A:m×n 阶的雅克比矩阵,m:测量值的个数 A:m×n阶的雅克比矩阵,m:测量值的个数
Δ : n 维 向 量 \Delta:n维向量 Δ:n维向量a r g m i n Θ ( − l o g f ( Δ ) ) = a r g m i n Θ 1 2 ∣ ∣ A Δ − b ) ∣ ∣ 2 argmin_\Theta (-logf(\Delta))=argmin_\Theta \frac{1}{2}||A\Delta-b)||^2 argminΘ(−logf(Δ))=argminΘ21∣∣AΔ−b)∣∣2
此时的协防差为:
∣ ∣ Δ ∣ ∣ Σ 2 = Δ T Σ − 1 Δ = Δ T Σ − T / 2 Σ − 1 / 2 Δ = ∣ ∣ Σ − 1 / 2 Δ ∣ ∣ 2 ||\Delta||^2_Σ=\Delta^TΣ^{-1}\Delta=\Delta^TΣ^{-T/2}Σ^{-1/2}\Delta=||Σ^{-1/2}\Delta||^2 ∣∣Δ∣∣Σ2=ΔTΣ−1Δ=ΔTΣ−T/2Σ−1/2Δ=∣∣Σ−1/2Δ∣∣2
参数 Δ \Delta Δ:
迭代时,一旦找到当前的 Δ \Delta Δ,使用 Θ ⊕ Δ \Theta\oplus\Delta Θ⊕Δ作为下一次迭代值
⊕ : 一 般 为 加 法 , 但 是 在 用 四 元 数 做 3 D 旋 转 和 映 射 时 使 用 相 关 李 群 代 替 \oplus:一般为加法,但是在用四元数做3D旋转和映射时使用相关李群代替 ⊕:一般为加法,但是在用四元数做3D旋转和映射时使用相关李群代替
参数 A A A:
A为稀疏块矩阵,对应非线性高斯因子图在 Θ \Theta Θ处的线性化,与原非线性图一样,均在 Δ \Delta Δ处服从高斯分布,
定义函数: P ( Δ ) P(\Delta) P(Δ):
定义函数: P ( Δ ) = e − l o g f ( Δ ) = e − 1 2 ∣ ∣ A Δ − b ∣ ∣ 2 P(\Delta)=e^{-logf(\Delta)}=e^{- \frac{1}{2}||A\Delta-b||^2} P(Δ)=e−logf(Δ)=e−21∣∣AΔ−b∣∣2
A Δ − b A\Delta-b AΔ−b:可以使用Cholesky或者QR分解:
在 d Δ : Δ 的 微 分 为 0 时 d\Delta:\Delta的微分为0时 dΔ:Δ的微分为0时:
(1):Choleskyf分解得到 A T A = R T R A^TA=R^TR ATA=RTR
(2): y = R Δ y=R\Delta y=RΔ
可以得到正规方程,先求解y,(或使用QR分解正规方程)就可以得到更新 Δ \Delta Δ
A T A Δ = ( 1 ) A T b ⟺ R T y ( 1 ) = A b A^TA\Delta=^{(1)}A^Tb \iff R^Ty^{(1)}=A^b ATAΔ=(1)ATb⟺RTy(1)=Ab, -
最后得到GTSAM中的迭代求解方法(用直接方程求解器(Cholesky,QR)求解SLAM的平滑解的一般结构。)
(1): Θ \Theta Θ:
(2): Θ ′ = Θ ⊕ Δ \Theta'=\Theta\oplus\Delta Θ′=Θ⊕Δ:更新下一步
(3):step3-6步使用信赖区域法迭代求解
1. 添加测量值
2. 添加并初始化变量
3. 在(1)处线性化
4. 使用QR或者Cholesky分解
5. 求解Δ
6. 获得更新的估计值(2)
6.总结
上述迭代方法可以使用局部进行迭代,从而避免了批量处理,然而当加入了新的因子,变量顺序往往不是最优的,ISAM会进行周期性的批量分解,对变量重新排序并进行隐式分解,然而该方法只在批量处理中试探进行,不能得到线性最优解。
贝叶斯树
将状态估计文体直接转换为图模型解决,无需将因子图转换为稀疏矩阵,然后应用稀疏线性代数方法。
- 将因子图转换为贝叶斯网络(变量消除)
伪代码:变量消除法
(1): θ j \theta_j θj
(2): f j o i n t ( θ j , S j ) = Π i f i ( Θ I ) , ( Θ i : θ j 相 关 函 数 节 点 ) f_{joint}(\theta_j,S_j)=\Pi_if_i(\Theta_I),(\Theta_i:\theta_j相关函数节点) fjoint(θj,Sj)=Πifi(ΘI),(Θi:θj相关函数节点)
(3): f j o i n t ( θ j , S j ) = P ( θ j ∣ S j ) f n e w ( S j ) f_{joint}(\theta_j,S_j)=P(\theta_j|S_j)f_{new}(S_j) fjoint(θj,Sj)=P(θj∣Sj)fnew(Sj)
1.移除所有相邻与(1)相邻的函数节点,定义Sj,所有移除函数节点相关因子节点,除了(1)
2.得到联合概率密度矩阵(2)
3.使用链式规则,条件概率密度(3),
消除顺序见下图
原 始 函 数 节 点 : f ( x 1 ) , f ( x 1 , x 2 ) , f ( x 2 , x 3 ) , , f ( l 1 , l 1 ) , f ( l 1 , x 2 ) , f ( l 2 , x 3 ) 原始函数节点:f(x_1),f(x_1,x_2),f(x_2,x_3),,f(l_1,l_1),f(l_1,x_2),f(l_2,x_3) 原始函数节点:f(x1),f(x1,x2),f(x2,x3),,f(l1,l1),f(l1,x2),f(l2,x3)
原 始 因 子 节 点 : f ( x 1 ) , f ( x 2 ) , f ( x 2 ) , f ( l 1 ) , f ( l 2 ) 原始因子节点:f(x_1),f(x_2),f(x_2),f(l_1),f(l_2) 原始因子节点:f(x1),f(x2),f(x2),f(l1),f(l2)
消除顺序 l 1 − > l 2 − > x 1 − > x 2 − > x 3 a − > b − > c − > d − > e l_1->l_2->x_1->x_2->x_3\\ a->b->c->d->e l1−>l2−>x1−>x2−>x3a−>b−>c−>d−>e
结果为:I
l 1 : f j o i n t ( l 1 , x 1 , x 2 ) = P ( l 1 ∣ x 1 , x 2 ) P ( x 1 , x 2 ) l_1:f_{joint}(l_1,x_1,x_2)=P(l_1|x_1,x_2)P(x_1,x_2) l1:fjoint(l1,x1,x2)=P(l1∣x1,x2)P(x1,x2)
l 2 : f j o i n t ( l 2 , x 3 ) = P ( l 2 ∣ x 3 ) P ( x 3 ) l_2:f_{joint}(l_2,x_3)=P(l_2|x_3)P(x_3) l2:fjoint(l2,x3)=P(l2∣x3)P(x3)
x 1 : f j o i n t ( x 1 , x 2 ) = P ( x 1 ∣ x 2 ) P ( x 2 ) x_1:f_{joint}(x_1,x_2)=P(x_1|x_2)P(x_2) x1:fjoint(x1,x2)=P(x1∣x2)P(x2)
x 2 : f j o i n t ( x 2 , x 3 ) = P ( x 2 ∣ x 3 ) P ( x 3 ) x_2:f_{joint}(x_2,x_3)=P(x_2|x_3)P(x_3) x2:fjoint(x2,x3)=P(x2∣x3)P(x3)
x 3 : f j o i n t ( x 3 ) x_3:f_{joint}(x_3) x3:fjoint(x3)
 2. 高斯消元
2. 高斯消元
上述使用 f j o i n t ( θ j , S j ) = P ( θ j ∣ S j ) f n e w ( S j ) f_{joint}(\theta_j,S_j)=P(\theta_j|S_j)f_{new}(S_j) fjoint(θj,Sj)=P(θj∣Sj)fnew(Sj)可以使用Gram-Schmidt或者Householder分解求解,所以变量消除法等价于QR隐式分解
定义高斯联合概率密度为:
Δ j ∈ R , 待 消 除 因 子 节 点 \Delta_j\in R,待消除因子节点 Δj∈R,待消除因子节点
s j ∈ R n j , 点 集 S j 的 长 度 为 n j s_j\in R^{n_j},点集S_j的长度为n_j sj∈Rnj,点集Sj的长度为nj
m j : 所 有 测 量 值 中 ( 因 子 节 点 ) 与 Δ j 相 连 的 个 数 m_j:所有测量值中(因子节点)与\Delta_j相连的个数 mj:所有测量值中(因子节点)与Δj相连的个数
a ∈ R m j , A S ∈ R m j × n j , b ∈ R m j a\in R^{m_j},A_S\in R^{m_j×n_j},b\in R^{m_j} a∈Rmj,AS∈Rmj×nj,b∈Rmj
f j o i n t ( Δ j , s j ) = e x p { − 1 2 ∣ ∣ a Δ j + A S s j − b ∣ ∣ 2 } f_{joint}(\Delta_j,s_j)=exp\{-\frac{1}{2}||a\Delta_j+A_Ss_j-b||^2\} fjoint(Δj,sj)=exp{−21∣∣aΔj+ASsj−b∣∣2}
当给定点集 s j s_j sj时,可以得到条件概率密度:
a † ( 伪 逆 ) = ( a T a ) − 1 a T a^†(伪逆)=(a^Ta)^{-1}a^T a†(伪逆)=(aTa)−1aT
r = a † A S r=a^†A_S r=a†AS
d = a † b d=a^†b d=a†b
P ( Δ j ∣ s j ) = e x p { − 1 2 ( Δ j + r s j − d ) 2 } P(\Delta_j|s_j)=exp\{-\frac{1}{2}(\Delta_j+rs_j-d)^2\} P(Δj∣sj)=exp{−21(Δj+rsj−d)2}
得到的边缘密度:
A ′ = A s − a ∗ r A'=A_s-a*r A′=As−a∗r
b ′ = b − a ∗ d b'=b-a*d b′=b−a∗d
f n e w ( S j ) = e x p ( − 1 2 ∣ ∣ A ′ s j − b ′ ∣ ∣ ) f_{new}(S_j)=exp(-\frac{1}{2}||A's_j-b'||) fnew(Sj)=exp(−21∣∣A′sj−b′∣∣)
-向量 r r r,和表量d,对应着贝叶斯网络的一个联合条件概率密度和平方根信息矩阵的单行,因次变量消除法的到的贝叶斯网络等价于变量消除的到的平方根信息矩阵。
-最后就变成了一个最小二乘问题:
–第一步:计算所有从树叶到树根的 Δ ∗ 定 义 所 有 函 数 \Delta *定义所有函数 Δ∗定义所有函数(在构造贝叶斯过程中完程)
–第二步:在从上到下一次性检索所有最优解,,得到这些解构成的 Δ \Delta Δ:
(通过 P ( Δ j ∣ s j ) P(\Delta_j|s_j) P(Δj∣sj),求解每一个 Δ j \Delta_j Δj)
Δ j : 在 稀 疏 线 性 代 数 称 之 为 反 置 换 \Delta_j:在稀疏线性代数称之为反置换 Δj:在稀疏线性代数称之为反置换
Δ j = d − r s j \Delta_j=d-rs_j Δj=d−rsj
3. 创建贝叶斯树
-由贝叶斯网络消元导出,以便可以更好的进行迭代和边缘化
-贝叶斯树是有向的,使用因子概率密度保存
-定义条件函数(联合概率密度拆分):
C k : 团 , 两 点 之 间 有 边 点 的 集 合 C_k:团,两点之间有边点的集合 Ck:团,两点之间有边点的集合
Π k : C k 的 父 团 \Pi_k:C_k的父团 Πk:Ck的父团
S k = C k ∩ Π k S_k=C_k\cap \Pi_k Sk=Ck∩Πk
-定义联合概率密度为:
Θ i : θ j 相 关 函 数 节 点 \Theta_i:\theta_j相关函数节点 Θi:θj相关函数节点
P ( Θ ) = Π k P ( F k ∣ S k ) P(\Theta)=\Pi_kP(F_k|S_k) P(Θ)=ΠkP(Fk∣Sk)
-根节点的 F r F_r Fr为空,容易求解
-因为 S k 总 是 Π k S_k总是 \Pi_k Sk总是Πk的点集,隐私有向边在图中的定义与贝叶斯相同,具有相同的条件概率函数。
-将贝叶斯网络转换为贝叶斯树的步骤(伪代码):
#这里我们已经将因子图转换为贝叶斯网络,使用贝叶斯网络构造,消除的顺序与因子图变为贝叶斯相反
对于每一个贝叶斯网络的条件函数,使用反向消元顺序进行转换
if no parent(S_j={})
从包含根节点θj的团Fr开始
else
找到父团Cp,将第一个被消元的Sj作为条件变量
if 如果父节点Cp中Fp和Sp的并集,等于分解节点S_j的条件变量
将条件变量插入团Cp
else
创建一个新的团C'作为Cp的子团
 已知:
已知:
l 1 : f j o i n t ( l 1 , x 1 , x 2 ) = P ( l 1 ∣ x 1 , x 2 ) P ( x 1 , x 2 ) l_1:f_{joint}(l_1,x_1,x_2)=P(l_1|x_1,x_2)P(x_1,x_2) l1:fjoint(l1,x1,x2)=P(l1∣x1,x2)P(x1,x2)
l 2 : f j o i n t ( l 2 , x 3 ) = P ( l 2 ∣ x 3 ) P ( x 3 ) l_2:f_{joint}(l_2,x_3)=P(l_2|x_3)P(x_3) l2:fjoint(l2,x3)=P(l2∣x3)P(x3)
x 1 : f j o i n t ( x 1 , x 2 ) = P ( x 1 ∣ x 2 ) P ( x 2 ) x_1:f_{joint}(x_1,x_2)=P(x_1|x_2)P(x_2) x1:fjoint(x1,x2)=P(x1∣x2)P(x2)
x 2 : f j o i n t ( x 2 , x 3 ) = P ( x 2 ∣ x 3 ) P ( x 3 ) x_2:f_{joint}(x_2,x_3)=P(x_2|x_3)P(x_3) x2:fjoint(x2,x3)=P(x2∣x3)P(x3)
x 3 : f j o i n t ( x 3 ) x_3:f_{joint}(x_3) x3:fjoint(x3)
ex:
step:1, x 3 , x 3 : f j o i n t ( x 3 ) x_3, x_3:f_{joint}(x_3) x3,x3:fjoint(x3)
S 1 = { } , 找 到 包 含 x 3 的 子 团 F r ( 没 有 创 建 ) S_1=\{\},找到包含x_3的子团F_r(没有创建) S1={},找到包含x3的子团Fr(没有创建)
step:2 , x 2 : f j o i n t ( x 2 , x 3 ) = P ( x 2 ∣ x 3 ) P ( x 3 ) x_2:f_{joint}(x_2,x_3)=P(x_2|x_3)P(x_3) x2:fjoint(x2,x3)=P(x2∣x3)P(x3)
P ( x 3 ) , S 1 = { } , 找 到 包 含 x 3 的 子 团 F r P(x_3),S_1=\{\},找到包含x_3的子团F_r P(x3),S1={},找到包含x3的子团Fr
P ( x 2 ∣ x 3 ) , S 2 = x 3 , F 2 = x 2 , C p = x 3 , C p = F 2 , 将 S 2 , 插 入 团 C p = x 2 , x 3 P(x_2|x_3),S_2=x_3,F_2=x_2,C_p=x_3,C_p=F_2,将S_2,插入团Cp=x_2,x_3 P(x2∣x3),S2=x3,F2=x2,Cp=x3,Cp=F2,将S2,插入团Cp=x2,x3
step:3 , x 1 : f j o i n t ( x 1 , x 2 ) = P ( x 1 ∣ x 2 ) P ( x 2 ) x_1:f_{joint}(x_1,x_2)=P(x_1|x_2)P(x_2) x1:fjoint(x1,x2)=P(x1∣x2)P(x2)
P ( x 2 ) , S 1 = { } , 找 到 包 含 x 2 的 子 团 F r P(x_2),S_1=\{\},找到包含x_2的子团F_r P(x2),S1={},找到包含x2的子团Fr
P ( x 1 ∣ x 2 ) , S 2 = x 2 , F 2 = x 1 , C p = x 2 , x 3 , C p ≠ F 2 , C p = x 1 : x 2 , 作 为 C p 子 团 插 入 P(x_1|x_2),S_2=x_2,F_2=x_1,C_p=x_2,x_3,C_p\neq F_2,Cp=x_1:x_2,作为C_p子团插入 P(x1∣x2),S2=x2,F2=x1,Cp=x2,x3,Cp=F2,Cp=x1:x2,作为Cp子团插入
step:4 , l 2 : f j o i n t ( l 2 , x 3 ) = P ( l 2 ∣ x 3 ) P ( x 3 ) l_2:f_{joint}(l_2,x_3)=P(l_2|x_3)P(x_3) l2:fjoint(l2,x3)=P(l2∣x3)P(x3)
P ( x 3 ) , S 1 = { } , 找 到 包 含 x 3 的 子 团 F r P(x_3),S_1=\{\},找到包含x_3的子团F_r P(x3),S1={},找到包含x3的子团Fr
P ( l 2 ∣ x 3 ) , S 2 = x 3 , F 2 = l 2 , C p = x 2 , x 3 , C p ≠ F 2 , C p = l 2 : x 2 , 作 为 C p 子 团 插 入 P(l_2|x_3),S_2=x_3,F_2=l_2,C_p=x_2,x_3,C_p\neq F_2,Cp=l_2:x_2,作为C_p子团插入 P(l2∣x3),S2=x3,F2=l2,Cp=x2,x3,Cp=F2,Cp=l2:x2,作为Cp子团插入
step:5 , l 1 : f j o i n t ( l 1 , x 1 , x 2 ) = P ( l 1 ∣ x 1 , x 2 ) P ( x 1 , x 2 ) l_1:f_{joint}(l_1,x_1,x_2)=P(l_1|x_1,x_2)P(x_1,x_2) l1:fjoint(l1,x1,x2)=P(l1∣x1,x2)P(x1,x2)
P ( x 1 , x 2 ) , S 1 = { } , 找 到 包 含 x 1 , x 2 的 子 团 F r P(x_1,x_2),S_1=\{\},找到包含x_1,x_2的子团F_r P(x1,x2),S1={},找到包含x1,x2的子团Fr
P ( l 2 ∣ x 1 , x 2 ) , S 2 = l 2 , F 2 = x 1 , x 2 ; 将 x 1 , x 2 前 挪 , C p = x 1 , x 2 , C p = F 2 , l 1 插 入 子 团 C p P(l_2|x_1,x_2),S_2=l_2,F_2=x_1,x_2;将x_1,x_2前挪,C_p=x_1,x_2,C_p= F_2,l_1插入子团C_p P(l2∣x1,x2),S2=l2,F2=x1,x2;将x1,x2前挪,Cp=x1,x2,Cp=F2,l1插入子团Cp
- 增量推理
F : 贝 叶 斯 树 平 方 根 信 息 矩 阵 F:贝叶斯树平方根信息矩阵 F:贝叶斯树平方根信息矩阵
已有一个子团 f ′ ( x j , x j ′ ) f'(x_j,x'_j) f′(xj,xj′),当一个新的测量值添加子团,只有 x j , x j ′ x_j,x'_j xj,xj′分别与其root的的路径受到影响,其他不包含 x j , x j ′ x_j,x'_j xj,xj′子团不受影响,将受影响的贝叶斯树转换为因子图,再将新值添加进去,这里采用一种新的次序进行消元:
x 1 , x 2 , x 3 : 位 置 姿 态 x_1,x_2,x_3:位置姿态 x1,x2,x3:位置姿态
l 1 , l 2 , 路 标 观 测 点 l_1,l_2,路标观测点 l1,l2,路标观测点
a:原始问题的因子图,A:因子图的雅可比矩阵关系
b:因子图消元得到的贝叶斯网络 R:因子图消元得到的平方根信息矩阵,消元顺序 l 1 , . . . , l n , x 1 , . . . , x n l_1,...,l_n,x_1,...,x_n l1,...,ln,x1,...,xn
c:贝叶斯树与平方根信息矩阵R的关系,(贝叶斯树将信息矩阵R描述为描述为团结构的贝叶斯结构)
//更新
输入:F:贝叶斯树 f':新的线性因子
输出:F':更新后的贝叶斯树
1.移除顶部的贝叶斯数并将其重构为因子图
(1)对于每一个受新因素影响的变量,去掉相应的团和其到root的贝叶斯树。
(2)使用F(orgh) 存储剩下的孤立子树
2.添加新的因子到f'到第一步得到的因子图
3.将因子图顺序重构
4.消除变量(将因子图转换为贝叶斯网络),重新创建新的贝叶斯树(构造贝叶斯树的方法)
5.F(orgh) 插入重构的网络
实例

a:原始贝叶斯树
b:装化为因子图, x 1 , x 2 x_1,x_2 x1,x2蓝线表示添加了一个回环, l 2 l_2 l2没有受到影响
c:转换为贝叶斯网络
d更新后的贝叶斯树
已知:
l 1 : f j o i n t ( l 1 , x 1 , x 2 ) = P ( l 1 ∣ x 1 , x 2 ) P ( x 1 , x 2 ) l_1:f_{joint}(l_1,x_1,x_2)=P(l_1|x_1,x_2)P(x_1,x_2) l1:fjoint(l1,x1,x2)=P(l1∣x1,x2)P(x1,x2)
x 1 : f j o i n t ( x 1 , x 2 , x 3 ) = P ( x 1 ∣ x 2 , x 3 ) P ( x 2 , x 3 ) x_1:f_{joint}(x_1,x_2,x_3)=P(x_1|x_2,x_3)P(x_2,x_3) x1:fjoint(x1,x2,x3)=P(x1∣x2,x3)P(x2,x3)
x 2 : f j o i n t ( x 2 , x 3 ) = P ( x 2 ∣ x 3 ) P ( x 3 ) x_2:f_{joint}(x_2,x_3)=P(x_2|x_3)P(x_3) x2:fjoint(x2,x3)=P(x2∣x3)P(x3)
x 3 : f j o i n t ( x 3 ) x_3:f_{joint}(x_3) x3:fjoint(x3)
step:1, x 3 , x 3 : f j o i n t ( x 3 ) x_3, x_3:f_{joint}(x_3) x3,x3:fjoint(x3)
S 1 = { } , 找 到 包 含 x 3 的 子 团 F r ( 没 有 创 建 ) S_1=\{\},找到包含x_3的子团F_r(没有创建) S1={},找到包含x3的子团Fr(没有创建)
step:2 , x 2 : f j o i n t ( x 2 , x 3 ) = P ( x 2 ∣ x 3 ) P ( x 3 ) x_2:f_{joint}(x_2,x_3)=P(x_2|x_3)P(x_3) x2:fjoint(x2,x3)=P(x2∣x3)P(x3)
P ( x 3 ) , S 1 = { } , 找 到 包 含 x 3 的 子 团 F r P(x_3),S_1=\{\},找到包含x_3的子团F_r P(x3),S1={},找到包含x3的子团Fr
P ( x 2 ∣ x 3 ) , S 2 = x 3 , F 2 = x 2 , C p = x 3 , C p = F 2 , 将 S 2 , 插 入 团 C p = x 2 , x 3 P(x_2|x_3),S_2=x_3,F_2=x_2,C_p=x_3,C_p=F_2,将S_2,插入团Cp=x_2,x_3 P(x2∣x3),S2=x3,F2=x2,Cp=x3,Cp=F2,将S2,插入团Cp=x2,x3
step:3 , x 1 : f j o i n t ( x 1 , x 2 , x 3 ) = P ( x 1 ∣ x 2 , x 3 ) P ( x 2 , x 3 ) x_1:f_{joint}(x_1,x_2,x_3)=P(x_1|x_2,x_3)P(x_2,x_3) x1:fjoint(x1,x2,x3)=P(x1∣x2,x3)P(x2,x3)
P ( x 2 , x 3 ) , S 1 = { } , 找 到 包 含 x 2 , x 3 的 子 团 F r P(x_2,x_3),S_1=\{\},找到包含x_2,x_3的子团F_r P(x2,x3),S1={},找到包含x2,x3的子团Fr
P ( x 1 ∣ x 2 , x 3 ) , S 2 = x 2 , x 3 , F 2 = x 1 , C p = x 2 , x 3 , C p = F 2 插 入 子 团 C p = x 1 , x 2 , x 3 P(x_1|x_2,x_3),S_2=x_2,x_3,F_2=x_1,C_p=x_2,x_3,C_p= F_2插入子团C_p=x_1,x_2,x_3 P(x1∣x2,x3),S2=x2,x3,F2=x1,Cp=x2,x3,Cp=F2插入子团Cp=x1,x2,x3
step:4 , l 2 : f j o i n t ( l 1 , x 1 , x 2 ) = P ( l 1 ∣ x 1 , x 2 ) P ( x 1 , x 2 ) l_2:f_{joint}(l_1,x_1,x_2)=P(l_1|x_1,x_2)P(x_1,x_2) l2:fjoint(l1,x1,x2)=P(l1∣x1,x2)P(x1,x2)
P ( x 1 , x 2 ) , S 1 = x 1 , x 2 , 找 到 包 含 x 1 , x 2 的 子 团 F r P(x_1,x_2),S_1=x_1,x_2,找到包含x_1,x_2的子团F_r P(x1,x2),S1=x1,x2,找到包含x1,x2的子团Fr
P ( l 1 ∣ x 1 , x 2 ) , S 2 = x 1 , x 2 , F 2 = l 1 , C p = x 1 , x 2 , x 3 , C p ≠ F 2 , C p = l 1 : x 1 , x 2 作 为 C p 子 团 插 入 P(l_1|x_1,x_2),S_2=x_1,x_2,F_2=l_1,C_p=x_1,x_2,x_3,C_p\neq F_2,Cp=l_1:x_1,x_2作为C_p子团插入 P(l1∣x1,x2),S2=x1,x2,F2=l1,Cp=x1,x2,x3,Cp=F2,Cp=l1:x1,x2作为Cp子团插入
- 增量顺序(COLAMD)列最近最小排序
-选择一种好的变量顺序可以加速稀疏矩阵求解诶,在贝叶斯树中是一样的。
-贝叶斯树中团的规模越大,填充时计算速度越慢
-子图、生成子图、导出子图
-环
-本文所有贝叶斯网络均匀弦图,既有完美的消除序列。
-寻找最优变量顺序时及其困难的(NP问题),可以使用列最小近似角度求解(column approximate minimum degree,COLMAD)最优顺序
-在进行增量推理时,变量可以在每次更新、消除时重新排序(图模型况阶),对于贝叶斯树只需要找到其中受影响的部分,对齐进行优化排序,gtsam提供了一增量排序方法。
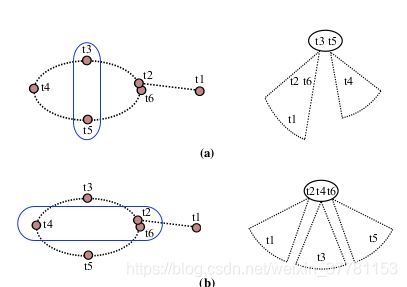
- 理解排序对后续更新的影响
对于一个循环实例(上图),可以使用两种方法进行切割:
-a:垂直切分,不包括回环
-b:水平切分 包括回环
两者实际上求解是相等,然而再增量模型中,a没有包含最新变量 t 6 t6 t6,增量更新时, t 6 t6 t6会在树模型的更深处,然而对于b,只需要更新根(包含最新的变量),显然b更加高效。相应的问题在应用COLAMD时叶会出现,在SLAM中,我们希望一系列新的测量值与最近的历史相连(比如,仍在传感器范围内的路标、相邻位姿),其代价表示为更新中受影响的树大小,只要更新的值距离根足够近,而COLAMD没有考虑到这点,文中提出了带约束的COLAMD法:强制最近更新的变量排在最后面,并且使用COLAMD。
下图为效果
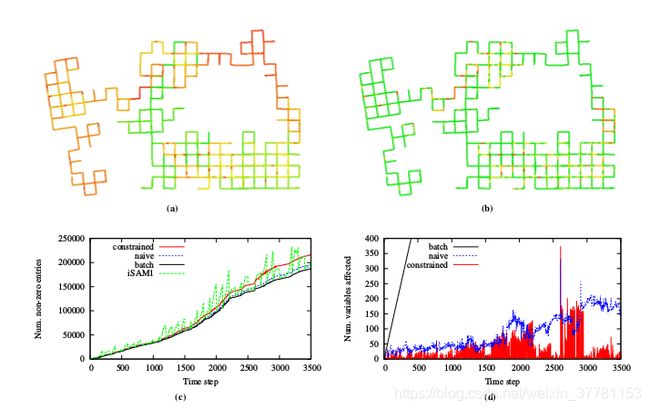 a,b,为使用曼哈顿数据进行测试,中路线越红表示计算量越大
a,b,为使用曼哈顿数据进行测试,中路线越红表示计算量越大
ISAM2
-假设噪声为高斯噪声,该算法使用一系列的非线性因子用来估计变量(位置、路标)随时间变换的增量。
-在上文中已经解决了贝叶斯树如何更新,ISAM2解决之后的问题:如何对非线性因子进行线性化,为了保证高效性,只在改变的变量部分进行
- 平滑再线性化(Fluid Relinearization)
跟踪每个able的线性化点的有效性,并且仅在需要时重新线性化。对于选择重新线性化的变量,必须从贝叶斯树中删除所有相关信息,并用重新线性化相应的原始非线性因子来代替。对于被重新消除的团,我们还必须考虑从其子树中传递的任何边缘因子。在消除过程中缓存这些边缘因子,允许从树的中间重新开始消除过程,而不必重新消除整个系统。
步骤如下:
-通过给定阈值 β : 估 计 值 与 线 性 点 的 偏 差 \beta:估计值与线性点的偏差 β:估计值与线性点的偏差
-需要考虑不同变量的单位,Manhattan dataset 中 β = 0.1 \beta=0.1 β=0.1
(1): Θ \Theta Θ
(2): β : J = { Δ j ∈ Δ ∣ Δ j > β } \beta:J=\{\Delta_j \in \Delta|\Delta_j>\beta\} β:J={Δj∈Δ∣Δj>β}
(3): Θ J = Θ J ⊕ Δ J \Theta_J=\Theta_J\oplus\Delta_J ΘJ=ΘJ⊕ΔJ:
原始版本:平滑再线性化
输入:线性化的点(1),估计值与线性点的偏差:∆
输出:更新后的(1),标记好的 团M
1.将所有高于阈值的变量标记为∆:β:(2)
2.更新所有被标记的变量:(3)
3.标记是团M,所有涉及到变量(1)的团和祖先团
更新所有受到影响的团的步骤,与之前更新贝叶斯树不同,也包括相性平滑区域,总体上
输入:贝叶斯树F,非线性因子f1,受影响的变量f2
输出:更新后的保额也似数F'
1.移除顶部的贝叶斯数:
(a):移除所有与f2相关的团,移除所有父团到根团的
(b):存储其余不相关的子团 F(orph)
2.重新线性化所有需要创建的顶部子团
3.将F(orph)内包含的线性因子添加缓存
4.带约束的CLOMAD重新排序
5.对因子消元,并创建贝叶斯树
6.将F(orph)插入新的贝叶斯树
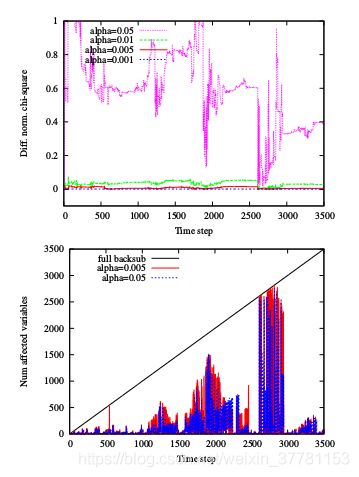
下图 β \beta β选取,
-上边 β \beta β对精度的影响爱嗯,
-下边 β \beta β对计算成本的影响爱,大于峰值超出曲线步分都会重新线性化$

- 部分状态更新(Partial State Updates)
-求得精确的解,不许要对所有相关变量求解,虽然更新贝叶斯时只影响顶部的团,但是实际变量的估计值发生变化仍会传播到子树。但是顶部的影响往往是有限的,当没有大的回环存在时,新的测量值只影响局部值,更远的部分保持不变(将整个贝叶斯树比喻为一个房子,在一个房间内进行的测量通常不会影响先前获得的其他房间的估计值),因此可以减少计算成本。
-如何求解只更新实际变化的变量:从树的根节点开始,获取向量 Δ ( 标 记 所 有 变 化 量 , 用 来 线 性 化 点 Θ ) \Delta(标记所有变化量,用来线性化点\Theta) Δ(标记所有变化量,用来线性化点Θ),递归处理所有子团,直到子团中不包含任何∆与变化量超过阈值 α \alpha α中的值,
(1) Θ \Theta Θ
//部分状态变量更新,求解非线性贝叶斯树作为返回值,并更新当前线性化点(1)的差值∆
输入:贝叶斯数F
输出:更新后的∆
从根团开始Cr=Fr
1.if Ck=Fk:Sk
计算前置变量Fk的∆k:使用条件概率P(Fk|Sk)
2.对于所有 ∆kj>α:递归处理每一个子团
下 图 : α 对 于 误 差 和 求 解 速 度 影 响 下图:\alpha对于误差和求解速度影响 下图:α对于误差和求解速度影响
3. 算法与复杂度
-总结ISAM2的算法流程如下:
(1): Θ \Theta Θ
(2): Θ ′ \Theta' Θ′
(3): F = ϕ 空 集 合 , Θ = ϕ , f = Θ F=\phi空集合,\Theta=\phi,f=\Theta F=ϕ空集合,Θ=ϕ,f=Θ
(4): Θ ′ = Θ ∪ Θ ′ \Theta'=\Theta∪\Theta' Θ′=Θ∪Θ′
(5): Θ = Θ ⊕ Δ \Theta=\Theta\oplus\Delta Θ=Θ⊕Δ
输入/输出:贝叶斯树F,非线性因子f,线性化点(),更新∆
输入:新的非线性因子f',新的变量线性点(2)
初始化:(3)
1.添加新的因子:f:=f∪f'
2.初始化新的变量(2)并且有(4)
3.进行平滑再线性化,获取所有标记的M
4.使用F,M,对所有受到影响的因子消元,重新构造贝叶斯树
5.求解对子数影响大的集合∆(向量)
6.估计当前值(5)