多相机与激光雷达外参标定
内容目录
-
-
- 算法大致流程
- 使用的标定板
- Velodyne激光扫描器及矫正
- Ladybug3全向摄像机
-
- 三维激光扫描仪与全向摄像机系统的外参校准
- 最少需要的视角
-
算法大致流程
参考论文:Extrinsic Calibration of a 3D Laser Scanner and an
Omnidirectional Camera
论文代码:https://github.com/SubMishMar/cam_lidar_calib
算法大致流程:
- 利用RANSAC算法计算出平面方程,利用方位角计算出激光雷达扫描到的障碍物到激光雷达的距离,利用真实距离数据,最小化误差,从而对激光雷达进行校准。
- 利用线性优化算法计算出每个相机坐标系下的法向量在head坐标系下的坐标。
- 利用法向量数据,最小化投影误差,计算得到 l h R ^h_l R lhR和 h t h l ^h t_{hl} hthl。
使用的标定板
外参估计需要相机和激光数据的共同观测特征,这些特征可以很容易的从各自的传感器中得到。在外参矫正的过程中,我们使用了贴在平面之上的棋盘格。使用棋盘格的原因主要有两个:
- 棋盘格上的特征容易提取
- 平面特征可以很容易的从三维点云中提取
实验使用的外部矫正传感器和感知传感器(Velodyne HDL-64E 3D laser scanner and Pointgrey Ladybug3 omnidirectional camera)如图所示
Velodyne激光扫描器及矫正
Velodyne HDL-64E是一种可以进行自主导航、定位、地图构建,具有高清晰度的激光雷达。该激光雷达使用短时间的激光脉冲,并且利用高灵敏度的光电探测器得到激光反射出去到反射回来的时间。利用往返时间TOF计算出每个激光脉冲击中位置距离激光雷达的距离 D l D_l Dl。
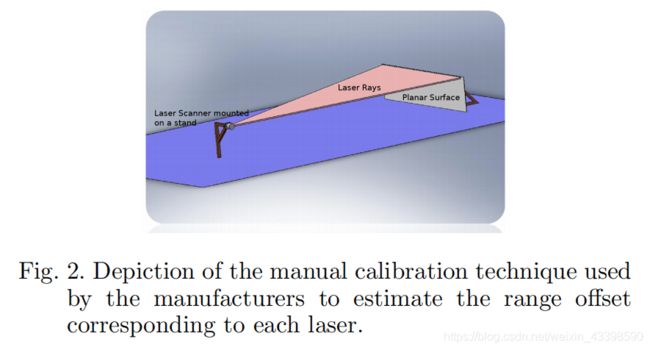
HDL-64E拥有两个激光块,其中每一个激光块包括32个激光二级管,中间有激光探测器。每个激光二极管以预定的垂直角度进行校准,造成了26.8度的垂直时间。整个单元可以围绕其垂直坐标轴以15Hz的速度旋转,并且提供360度方位角的视野。计算出的范围 D l D_l Dl包括由于TOF计算中误差产生的偏差,因此有一个大小为 δ D \delta D δD的偏差。HDL-64E的制造商,提供了一个每一个激光的矫正值来补偿距离测量的误差。他们使用图片2中描述的矫正装置来手动矫正每一个激光的范围来得到 δ D \delta D δD矫正的近似值。
激光扫描仪安装在墙上的支架上,并且通过手动测量墙和激光扫描仪之间的距离来计算距离测量的偏差
δ D = D m − D l \delta D = D_m - D_l δD=Dm−Dl
其中 D m D_m Dm是手动测量的雷达与墙之间的距离, D l D_l Dl使用TOF计算出来的距离.
激光雷达的内在参数会很大的影响激光雷达的外参矫正。因此,激光雷达的矫正是非常重要的。我们在进行外参矫正之前,我们提出了一个鲁棒性很好的方法来很好的得到 δ D \delta D δD。我们的方法只需要用户将安装有激光扫描仪的平台放在平面之前,并且记录范围测量结果。现在,如果我们使用在
记录激光传感器在平面不同位置的激光测量值。如果我们使用 δ D \delta D δD矫正并考虑墙上的点,这些点应该都是共平面的。但是由于 δ D \delta D δD的矫正是不精确的,所以这些点在平面上重投影的误差是显著的。因此,我们可以最小化每个激光器的再投影误差 δ D \delta D δD。我们使用RANSAC来估计平面方程来拟合该平面。主要步骤如下:
-
产生一个包括目标平面的框,并且选出可能在框内激光点 { Q ~ l i ; t = 1 , 2 , ⋯ , N } \{\widetilde{Q}_l^i;t=1,2,\cdots,N\} {Q li;t=1,2,⋯,N}。
-
利用这些选出的激光点,传入RANSAC平面拟合算法,这个算法将最佳拟合平面的线的集合(激光参考系中三维点)返回
RANSAC算法基本假设: RANSAC算法的基本假设是样本中包含正确数据(inliers,可以被模型描述的数据),也包含异常数据(Outliers,偏离正常范围很远、无法适应数学模型的数据),即数据集中含有噪声。这些异常数据可能是由于错误的测量、错误的假设、错误的计算等产生的。同时RANSAC也假设,给定一组正确的数据,存在可以计算出符合这些数据的模型参数的方法。
RANSAC算法流程如下:
- 从 { Q ~ l i ; t = 1 , 2 , ⋯ , N } \{\widetilde{Q}_l^i;t=1,2,\cdots,N\} {Q li;t=1,2,⋯,N}随机选取三个点;
- 计算出这三个点对应的平面方程;
- 找到所有满足该方程的点;
- 重复这个过程,直到找到包含最多点的平面。
-
让由RANSAC计算的平面由激光坐标系的原点开始参数化, N = [ n x , n y , n z ] N=[n_x,n_y,n_z] N=[nx,ny,nz], ∣ ∣ N ∣ ∣ ||N|| ∣∣N∣∣是从平面到原点的垂直距离。所以,如果 P ~ = [ X , Y , Z ] T \widetilde{P}=[X,Y,Z]^T P =[X,Y,Z]T是平面上的任意一个点,所以其在 N N N上的投影的长度就等于 N N N的长度,即:
P N = ∣ ∣ N ∣ ∣ 2 P N = ||N||^2 PN=∣∣N∣∣2
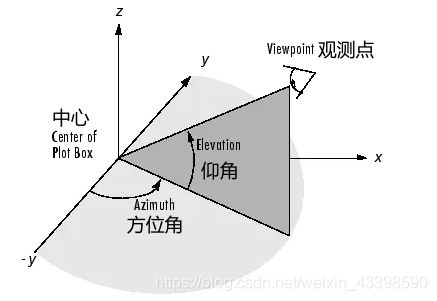
设 D D D是激光 i i i测量出的点的距离,并且 θ \theta θ和 ω \omega ω是对应的仰角和方位角,那么:
X = D cos θ sin ω Y = D cos θ cos ω Z = D sin θ \begin{aligned} X &= D\cos \theta \sin \omega\\ Y &= D\cos \theta \cos \omega\\ Z &= D\sin \theta \end{aligned} XYZ=Dcosθsinω=Dcosθcosω=Dsinθ
仰角和方位角具体定义如下:所以点到激光雷达位置的实际距离可以表示为如下形式:
D = ∥ N ∥ n x cos θ sin ω + n y cos θ cos ω + n z sin θ D=\frac{\|\mathbf{N}\|}{n_{x} \cos \theta \sin \omega+n_{y} \cos \theta \cos \omega+n_{z} \sin \theta} D=nxcosθsinω+nycosθcosω+nzsinθ∥N∥
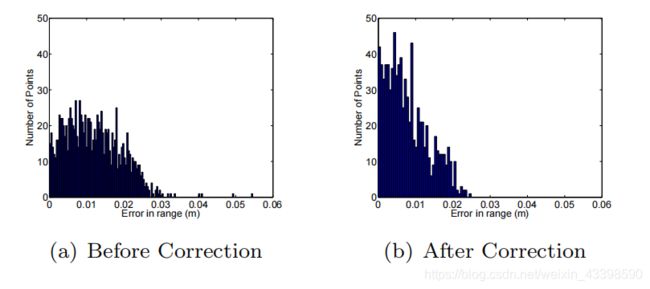
现在我们有了利用RANSAC算法得到的距离信息,并且我们可以得到 D m = D l + δ D D_m=D_l+\delta D Dm=Dl+δD,其中 δ D \delta D δD人工矫正得到的距离误差。在这里我们得到了偏移 δ D ′ \delta D' δD′,是利用64个雷达的均方误差计算所得:
δ D i ′ = argmin δ D i ′ ∑ i = 1 64 ∑ i = 1 n ∥ D i j − ( D l i j + δ D i ′ ) ∣ \delta D_{i}^{\prime}=\underset{\delta D_{i}^{\prime}}{\operatorname{argmin}} \sum_{i=1}^{64} \sum_{i=1}^{n} \| D_{i j}-\left(D_{l_{i j}}+\delta D_{i}^{\prime}\right) \mid δDi′=δDi′argmini=1∑64i=1∑n∥Dij−(Dlij+δDi′)∣
其中, D i j D_{ij} Dij是利用上式计算出的第 j j j个点到第 i i i个激光雷达的距离, D l i j D_{l_{ij}} Dlij是利用TOF算出的第 j j j个点到第 i i i个激光雷达的距离。具体的矫正效果如下图所示:
Ladybug3全向摄像机
Ladybug3是一个高分辨率的全向摄像系统。它有6个200万像素的摄像头,5个Ccd位于一个水平环形,一个垂直定位,使系统能够从80%以上的整个球体收集视频。相机由制造商的预先校准,得到单个相机的内在参数。此外,所有相机相对于一个被称为相机头的公共坐标系的刚体变换也是已知的。因此,我们需要估计相机头的位姿(方向和位置)(相对于一些局部参考系),这样我们就可以表示相机头框架中的任何三维点,然后表示到任何相机的坐标系。我们使用下面的方法计算相机头的位姿
三维激光扫描仪与全向摄像机系统的外参校准
利用线性优化方法得到平面方程(大致流程,详细见下文)
- 设平面方程在平面坐标系下为 Z = 0 Z=0 Z=0,这样就可以得到在该坐标系下平面上点的坐标,随机初始化旋转矩阵和平移向量。
- 利用最小化平面方程坐标系到相机平面的投影误差,使用用线性优化算法计算出旋转矩阵和平移向量。
- 利用点的位姿以及求出的旋转矩阵和平移向量得到每个相机坐标系下平面的法向量 N c i i \textbf{N}^{\textbf{i}}_{\textbf{c}_{\textbf{i}}} Ncii,再次转换得到相机head坐标系下的法向量为 N h i \textbf{N}^{\textbf{i}}_{\textbf{h}} Nhi。
外参校准需要系统观察多个姿态的平面模式(棋盘格),并且基于同时从摄像机和激光扫描仪得到的数据进行约束。目标平面的 法向量和目标平面上的激光点具有相关关系,限制了相机和激光扫描仪的相对位置和方向。我们知道平面本身坐标系中的目标平面的方程,为了方便,我们设定世界坐标系下的平面方程为 Z = 0 Z=0 Z=0。
设 P ~ w \widetilde{P}_w P w为任意一个世界坐标系下的坐标(这里指的是目标平面上的点的坐标,比如棋盘格上点的坐标)。 w c i R ^{c_i}_{w}R wciR是从世界坐标到相机坐标的正交旋转矩阵, c i t c i w ^{c_i}t_{c_iw} citciw是从世界坐标到相机坐标的平移向量。因此,从世界坐标到相机 c i c_i ci坐标转换的方程如下:
P ~ c i = w c i R P ~ w + c i t c i w \tilde{P}_{c_{i}}={ }_{w}^{c_{i}} R \tilde{P}_{w}+{ }^{\mathrm{c}_{i}} \mathbf{t}_{\mathbf{c}_{\mathbf{i}} \mathbf{w}} P~ci=wciRP~w+citciw
其中, P ~ c i \tilde{P}_{c_{i}} P~ci是同一个点在相机 c i c_i ci坐标系下的坐标。因为我们知道从相机 c i c_i ci坐标系到相机head坐标系的转换,所以可以得到在该点在相机head坐标系下的坐标如下:
P ~ h = c i h R P ~ w + c i t c i w \tilde{P}_h=^h_{c_i}R\tilde{P}_w + ^{c_i}t_{c_i w} P~h=cihRP~w+citciw
因此,我们可以将任意一个在世界坐标系下的坐标 P ~ w \tilde{P}_w P~w转换到相机head坐标系的 P ~ h \tilde{P}_{h} P~h。
针孔相机模型简介
对于针孔相机模型,一个三维点 P ~ w = [ X Y Z 1 ] T \tilde{P}_w=[X\ Y\ Z\ 1]^T P~w=[X Y Z 1]T和其对应的在图像上的投影 p ~ = [ u v 1 ] T \tilde{p}=[u\ v\ 1]^T p~=[u v 1]T可以由下列方法得到:
p ~ = K i [ w c i R c i t c i w ] ] P ~ w \tilde{p}=K_{i}\left[\begin{array}{l} \left. ^{c_i}_w R^{\mathbf{c}_{\mathbf{i}}} \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w}}}\right] \end{array}\right] \tilde{P}_{w} p~=Ki[wciRcitciw]]P~w
其中 ( w c i R , c i t c i w ) (^{c_i}_w R,^{c_i}t_{c_i w}) (wciR,citciw)是相机外参,是世界坐标系到相机 i i i坐标系到旋转和平移, K i K_i Ki是相机内参。
假设图像上的点的误差是独立同分布的,利用最小化 n n n个图像和 m m m个点的重投影误差,可以得到所需变换 w c i R , c i t c i w ^{c_i}_{w}R,^{c_i}t_{c_i w} wciR,citciw的最大似然估计,即满足 p ~ k j \tilde{p}_{kj} p~kj与 p ~ \tilde{p} p~之间的差值最小:
argmin w c i R , c i t c i w ∑ k = 1 n ∑ j = 1 m ∥ p ~ k j − K i [ c i w R c i t c i w ] P ~ j ∥ \underset{_{w}^{c_i} R,^{{\mathrm{c}}_{\mathrm{i}}} \mathbf{t}_{\mathrm{c}_{\mathrm{i}} \mathrm{w}}}{\operatorname{argmin}} \sum_{k=1}^{n} \sum_{j=1}^{m}\left\|\tilde{p}_{k j}-K_{i}\left[\begin{array}{c} c_{i} \\ w \end{array} R^{\mathbf{c}_{\mathbf{i}}} \mathbf{t}_{\mathbf{c}_{\mathbf{i}} \mathbf{w}}\right] \tilde{P}_{j}\right\| wciR,citciwargmink=1∑nj=1∑m∥∥∥∥p~kj−Ki[ciwRcitciw]P~j∥∥∥∥
这个算的东西有点像apriltag+slovepnp,可以求出相机坐标到世界坐标(平面坐标)的转换矩阵和平移向量
其中, w c i R ^{c_i}_{w}R wciR是旋转矩阵。如果 w c i R = [ r 1 , r 2 , r 3 ] ^{c_i}_{w}R=[r_1, r_2, r_3] wciR=[r1,r2,r3]而且 c i t c i w ^{c_i}t_{c_i w} citciw是从 c i c_i ci到 w w w的平移向量,我们可以将在相机 i \textbf{i} i坐标系下的平面方程写成:
r 3 ⋅ ( p + c i t c i w ) = 0 \mathbf{r}_{3} \cdot\left(\mathbf{p}+{ }^{\mathbf{c}_{\mathbf{i}}} \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w}}}\right)=0 r3⋅(p+citciw)=0
其中 p \textbf{p} p是原点到平面上任何一点的向量。
因此,在相机 i \textbf{i} i坐标系下,目标平面的法向量为:
N c i = ( r 3 ⋅ c i t c i w ) r 3 \mathbf{N}_{\mathbf{c}_{\mathbf{i}}}=\left(\mathbf{r}_{3} \cdot \mathbf{c}_{\mathbf{i}} \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w}}}\right) \mathbf{r}_{3} Nci=(r3⋅citciw)r3
其中, ∥ N c i ∥ = r 3 ⋅ c i t c i w \| \mathbf{N}_{\textbf{c}_{i}}\|=\mathbf{r}_{3} \cdot{\mathbf{c}_{\mathbf{i}}} \mathbf{t}_{\mathbf{c}_{\mathbf{i}} \mathbf{w}} ∥Nci∥=r3⋅citciw是从目标平面到第 i i i个相机的距离。因为我们知道了第 i i i个相机关于相机head的位姿。我们可以计算平面在相机head坐标系下的法向量 N h N_{h} Nh如下:
N h = c i h R N c i ∥ N c i ∥ ( ∥ N c i ∥ + N c i ⋅ h t hc i ) \textbf{N}_h = \frac{^h_{c_i}R\textbf{N}_{\textbf c_i}}{\|\textbf{N}_{\textbf{c}_i}\|}(\|\textbf{N}_{\textbf{c}_i}\|+\textbf{N}_{\textbf{c}_i}\cdot ^{\textbf{h}}\textbf{t}_{\textbf{hc}_{\textbf{i}}}) Nh=∥Nci∥cihRNci(∥Nci∥+Nci⋅hthci)
三维空间法线变换方法:
- 假设Model space中的某条切线向量是 T T T,法线向量是 N N N。那么由他们是垂直的可得到: T T N = 0 T^TN=0 TTN=0
- 假设他们变换到Eye space中后分别是 T ′ T' T′和 N ′ N' N′(这里假设切向量并不是由变换矩阵计算得到的,而是直接通过对模型表面进行几何分析计算得到的)。那么他们应该仍然是相互垂直的: T ′ T N ’ = 0 T'^TN’=0 T′TN’=0
- 假设切线向量和法线的变换矩阵为 M M M、 G G G。则有: ( M T ) T ( G N ) = 0 (MT)^T(GN)=0 (MT)T(GN)=0
- 进一步推出: T T M T G N = 0 T^TM^TGN=0 TTMTGN=0
- 由于 T T N = 0 T^TN=0 TTN=0,因此要满足成立条件需要 M T G = I M^TG=I MTG=I.因此: G = ( M − 1 ) T G=(M^{-1})^T G=(M−1)T
- 即:应用于法线向量的变换矩阵是顶点变换矩阵的逆转置矩阵。
在知道了目标平面在head坐标系下的法向量之后,我们就需要知道三维世界的点在平面上的坐标(坐标相对于激光雷达坐标系)。利用RANSAC算法,我们可以利用这些点计算出目标平面的法向量。这两个测量出的法向量为激光器和照相机之间所需的转换提供了约束。设 { P ~ j i ; i = 1 , 2 , ⋯ , n } \{\tilde{P}^i_j;i=1,2,\cdots,n\} {P~ji;i=1,2,⋯,n}为利用RANSAC算法所得到的平面上的点。那么这些点在head坐标系下的坐标应该为:
P ~ h i = l h R P ~ l i + h t h l \tilde{P}^i_h=^h_l R\tilde{P}^i_l+^ht_{hl} P~hi=lhRP~li+hthl
其中, l h R ^h_l R lhR和 h t h l ^h t_{hl} hthl是从激光雷达坐标系转换的相机head坐标系所需的旋转矩阵和平移。现在,如果我们发射一道激光落在平面上的任何一点 P ~ h i \tilde{P}^i_h P~hi,该点对应的向量关于法向量的投影等于平面到原点的距离。因此,对于 n n n种不同的关于目标平面的视角和 m m m个激光雷达的点,激光雷达-相机的外参可以通过最小化下列误差获得:
F = ∑ i = 1 n ∑ j = 1 m ( N h i ∥ N h i ∥ ⋅ P ~ h j − ∥ N h i ∥ ) 2 = ∑ i = 1 n ∑ j = 1 m ( N h i ∥ N h i ∥ ⋅ ( l h R P ~ l i + h t h l ) − ∥ N h i ∥ ) 2 \begin{aligned} F&=\sum_{i=1}^n \sum_{j=1}^{m}(\frac{\textbf{N}^{\textbf{i}}_{\textbf{h}}}{\|\textbf{N}^{\textbf{i}}_{\textbf{h}}\|}\cdot \tilde{P}^j_h-\|\textbf{N}^{\textbf{i}}_{\textbf{h}}\|)^2\\ &=\sum_{i=1}^n \sum_{j=1}^{m}(\frac{\textbf{N}^{\textbf{i}}_{\textbf{h}}}{\|\textbf{N}^{\textbf{i}}_{\textbf{h}}\|}\cdot (^h_l R\tilde{P}^i_l+^ht_{hl})-\|\textbf{N}^{\textbf{i}}_{\textbf{h}}\|)^2 \end{aligned} F=i=1∑nj=1∑m(∥Nhi∥Nhi⋅P~hj−∥Nhi∥)2=i=1∑nj=1∑m(∥Nhi∥Nhi⋅(lhRP~li+hthl)−∥Nhi∥)2
其中, N h i N^i_h Nhi是第 i i i个相机得到的在相机head坐标系下的平面的法向量, P ~ h j \tilde{P}^j_h P~hj是第 j j j个点在相机head坐标系下的位置。利用最小化投影误差,可以解决该线性优化问题得到 l h R ^h_l R lhR和 h t h l ^h t_{hl} hthl。
最少需要的视角
为什么法向量在进行坐标变换后不是一样的?
法向量方向是一样的,但是长度不一样。
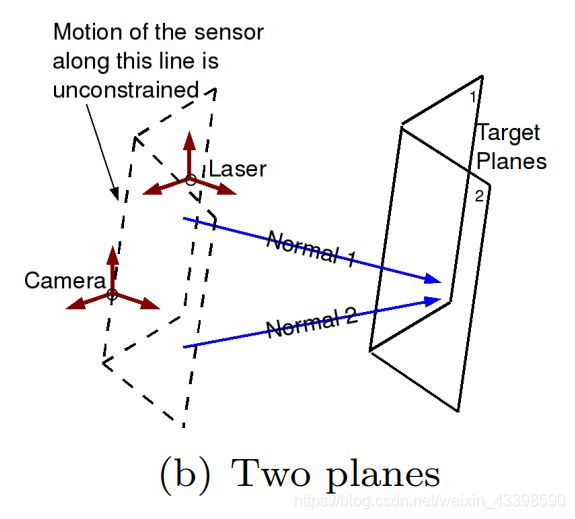
为了完全约束进行参数估计的优化问题,最少需要三个目标平面的非共面视图。图中的法向量指的是在每个相机坐标系下的法向量而不是转移到head坐标系下的法向量。
- 如果如下图所示的那样只有一个视图
当激光雷达沿着平行于目标平面的平面平移或以平行于目标平面法向量为轴旋转时,损失函数的值不会改变。因此,从单个视图得到的解并不收敛
综上所述,只有拥有三个以上的坐标时,才能进行标定。