【Focal Loss】Focal Loss理解
文章目录
- 1 Focal loss解决什么问题
-
- 1.1 正/负样本 定义
- 1.2 易/难分类样本 定义
- 1.3 怎么解决呢?
- 2 控制正负样本的加权 权重
- 3 控制易/难分类样本的加权 权重
- 4 两种权重控制方法合并
- 5 代码演示权重合并
- 6 Focal loss有点问题,继而引出GHM
- 7 感谢链接
1 Focal loss解决什么问题
简而言之,Focal loss用于解决样本不均衡问题。不均衡表现在两个方面:
- 正负样本数量不均衡
- 易分类的样本和难分类的样本数量不均衡
1.1 正/负样本 定义
一张图像可能会生成很多候选框,但其中只有很少一部分是包含目标的,有目标的就是正样本,没有目标的就是负样本。
1.2 易/难分类样本 定义
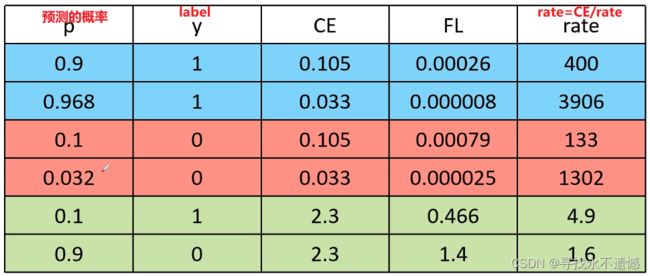
一个二分类问题,样本1属于类别1的概率(置信度)为0.9,样本2属于类别1的概率(置信度)为0.6,显然前者更可能是类别1,其就是易分类样本;后者有可能是类别1,只是概率比较低,称其为难分类样本。
1.3 怎么解决呢?
都用来算损失,一方数量多,主导了总损失?加权解决!
负样本数量多,权重系数小点,正样本数量少,权重系数大点;
易分类样本数量多,权重系数小点,难分类样本数量少,权重系数大点。
提出Focal loss的作者认为:负样本、易分类样本对模型提升效果很小,模型应该主动关注那些正样本、难分类样本。(GHM,Gradient Harmonized Single-stage Detector认为这个假设是有问题的,比如样本中的离群点)
2 控制正负样本的加权 权重
二分类中,常用的交叉熵损失CE:

可以利用如下 p t p_t pt简化交叉熵loss:
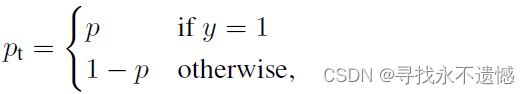
此时,交叉熵损失可写为:
![]()
想要降低负样本的影响,可以在常规的损失函数前增加一个系数 α t α_t αt。与 p t p_t pt类似,当label=1的时候, α t = α α_t=α αt=α;当label=otherwise的时候, α t = 1 − α α_t=1 - α αt=1−α, α α α的范围为0到1。
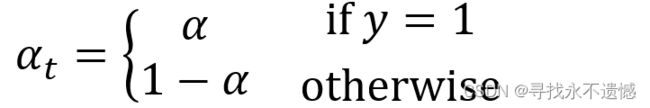
此时便可以通过设置 α α α实现控制正负样本对loss的贡献。
![]()
C E ( p , y , α ) = { − α ∗ l o g ( p ) 当 y = 1 时 − ( 1 − α ) ∗ l o g ( 1 − p ) o t h e r w i s e CE(p,y,α)=\begin{cases} -α * log(p) & 当y=1时 \\ -(1-α) * log(1-p) & otherwise \end{cases} CE(p,y,α)={−α∗log(p)−(1−α)∗log(1−p)当y=1时otherwise
注意:
- 理论上讲,正样本少,它对loss的贡献应该大,故alpha应该大于0.5;
- 但是,当与下面难易样本中操作结合到一起时,形式还逆转了,反而在这里要对正样本降权!大神论文中: α = 0.25 \alpha = 0.25 α=0.25,下面的 γ = 2 γ=2 γ=2。
3 控制易/难分类样本的加权 权重
一个二分类问题,样本1属于类别1的概率 p t p_t pt(置信度)为0.9,样本2属于类别1的概率 p t p_t pt(置信度)为0.6,理解为 是某个类的概率越大,其越容易分类。
容易分类的样本有很多,越容易, p t p_t pt越大,但每个容易样本对loss的贡献应该小点,可以用 ( 1 − p t ) (1-p_t) (1−pt)来作为其加权权重。
具体实现方式如下:
![]()
其中 ( 1 − p t ) γ (1-p_t)^{γ} (1−pt)γ称为调制系数(modulating factor)。
- 当 p t p_t pt趋于0时,调制系数趋于1,对于总的loss的贡献很大。当 p t p_t pt趋于1时,调制系数趋于0,对于总的loss的贡献很小。
- 当γ=0时,Focal loss就是传统的交叉熵损失,可以通过调整γ实现调制系数的改变。
4 两种权重控制方法合并
通过如下公式就可以实现控制正负样本的加权 权重和控制易分类和难分类样本的加权 权重。
5 代码演示权重合并
直接看代码注释,或者看下方b站链接的大佬视频讲解。
import numpy as np
# --------------------------------------------------------------------------#
# 理论上讲,正样本少,它对loss的贡献应该大,故alpha应该大于0.5
# 但是,与下面难易样本中操作结合到一起时,形式还逆转了,反而在这里要对正样本降权!
# 这里与论文中保持一致,alpha=0.25,γ=2
# --------------------------------------------------------------------------#
alpha = 0.25
y_true = np.array([1,0,1,0])
y_pred = np.array([0.9,0.1,0.6,0.6])
alpha_weights = [alpha if y==1 else 1-alpha for y in y_true]
print("alpha_weights:", alpha_weights)
p_t = np.zeros(4)
index1 = np.argwhere(y_true==1)
index0 = np.argwhere(y_true==0)
print("index1:", index1)
print("index0:", index0)
# -------------------------------------------------------#
# 越容易分,y_pred中概率越大,对贡献应该越小,故用 1-y_pred
# -------------------------------------------------------#
p_t[index1] = (1-y_pred[index1])**2
p_t[index0] = (y_pred[index0])**2
print("p_t:", p_t)
# -------------------------------#
# 两个权重相乘即得到最后的权重
# -------------------------------#
weights = p_t * alpha_weights
print("weights:", weights)
输出:
alpha_weights: [0.25, 0.75, 0.25, 0.75]
index1: [[0]
[2]]
index0: [[1]
[3]]
p_t: [0.01 0.01 0.16 0.36]
weights: [0.0025 0.0075 0.04 0.27 ]
这个结果,品,细品…
总之,Focal loss的关注顺序为:难分类的+样本少的;难分类的+样本多的;易分类的+样本少的;易分类的+样本多的。
6 Focal loss有点问题,继而引出GHM
Focal Loss让模型过多的关注特别难分类的样本是会有问题的。
例如,样本中有一些异常点、离群点(outliers)。
当模型为了拟合这些非常难拟合的离群点时,会存在过拟合的风险。
继而,引出GHM。
Focal Loss是 从置信度p 的角度入手衰减loss的。而GHM是 一定范围内置信度p的样本数量 来衰减loss的。
具体的,以后再学,可参考链接:
https://www.cnblogs.com/PythonLearner/p/13416128.html
https://zhuanlan.zhihu.com/p/80594704
7 感谢链接
https://blog.csdn.net/weixin_44791964/article/details/102853782
https://www.bilibili.com/video/BV1E7411J72R