模型剪枝一：Learning both Weights and Connections for Efficient Neural Networks

论文：https://arxiv.org/abs/1506.02626
代码：https://github.com/jack-willturner/DeepCompression-PyTorch
https://github.com/Guoning-Chen/SimplePruning-PyTorch

1 核心思想

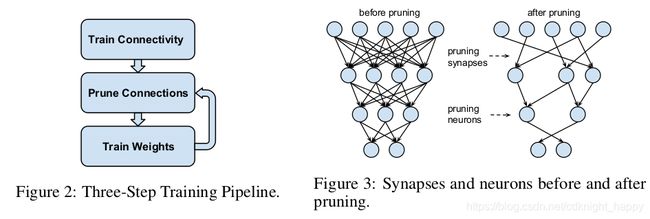
本文给出了一个模型剪枝的处理思路，如Fig.2所示，即将模型剪枝分为三步，分别为：

1. 按照常规方式训练网络，但训练结果中学到的不是权重值，而是各个连接的重要程度；
2. 按照预定的规则进行模型剪枝，舍弃掉重要度小于指定阈值的连接，将稠密连接的网络变成一个稀疏连接网络；
3. 对剪枝后的稀疏模型进行重训练，提升模型的识别精度，最后重训练这一步很关键，否则会造成识别准确度的大范围下降。

步骤2和步骤3要进行多轮的迭代。

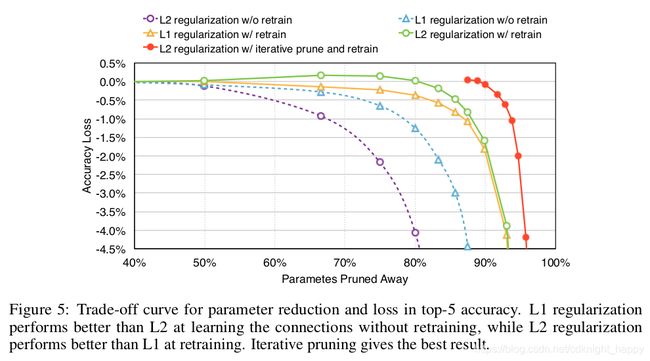
1.1 模型训练时不同正则化方法的区别

L1正则化倾向于将模型中的参数推向接近于0，L2正则化倾向于使模型中的权重值都是比较接近的接近于0的值。

实验结果上来看，对比L1和L2正则化，如果剪枝完成后不进行重训练，L1正则化的效果较好，这是因为剪枝过程剪去了本身值就很接近于0的连接，对于模型的准确率影响较小。而L2正则化中，各个权重值比较平均，剪去的部分对准确率的影响要更大一些。但是，如果剪枝后进行重训练，可以发现L2正则化的效果更好。所以这里建议使用L2正则化。

1.2 Dropout的比例

重训练的过程中也要使用dropout防止过拟合，但是因为重训练过程中，网络的参数量和连接数有所减小，因此也需要调整dropout的比例以适应新的网络参数量和连接量。因为重训练时网络的参数量和连接数有所减小，过拟合的风险也有所减小，所需的dropout比例也跟着减小了。

定量来描述的话，定义$C_i$为第$i$层的连接数，$C_{io}$表示原始网络第$i$层的连接数，$C_{ir}$表示剪枝后的网络重训练时第$i$层的连接数，$N_i$表示第$i$层的神经元数量。Dropout一般应用于全连接层，卷积层使用的是BN(https://www.cnblogs.com/lvdongjie/p/14088464.html、https://www.jianshu.com/p/0f75a9c51d44、https://www.zhihu.com/question/52426832、https://blog.csdn.net/z0n1l2/article/details/83662639)，所以这里以全连接层为例，有:

$C_i$是$N_i$的二次方。

由于dropout是作用于神经元的，进行模型剪枝后，神经元的数量减小，那么新的dropout的比例$D_r$应该变为：

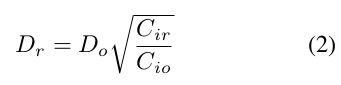
$D_o$表示模型初始训练过程中的dropout比例。

1.3 重训练过程中不要重新初始化模型

模型剪枝后进行重训练时，应该保持保留下来的神经元的原始参数，不要重新初始化这部分参数。这是因为CNN的协同适应性比较脆弱，一个模型首次训练时，适应梯度下降可以取得不错的结果。但是如果重新初始化某些层进行重新训练的效果往往不好。所以在剪枝后的模型重训练时，应该保留留下的神经元的原始权重值。

作者重训练的时候提到了一个技巧，对fc层进行了剪枝后，应该保持conv层参数不变只重训练fc层，反之亦然。

1.4 迭代剪枝

剪枝+重训练是一个基本处理单元，应该进行多轮迭代，每次减少一些连接数。

1.5 剪去神经元

每次剪枝都是剪的连接，如果某个神经元的输入连接或者输出连接变为了0，那么这个神经元就可以安全的移除了。因为这个神经元的输入或输出的连接数为0，那么该神经元在重训练过程中对于损失没有贡献，那么回传到它的输出或输入的梯度也为0，但是正则化项则会把这个神经元的参数往0拉，因此经过重训练过程中，输入或输出为0的神经元就被自动剪掉了。

2 实验

LeNet：
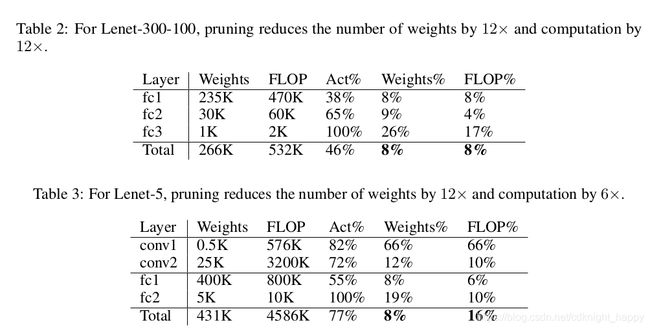For each layer of the network the table shows (left to right) the original number of weights, the number of floating point operations to compute that layer’s activations, the average percentage of activations that are non-zero, the percentage of non-zero weights after pruning, and the percentage of actually required floating point operations.

上面的实验也看出对于全连接层剪去的参数比例更大。

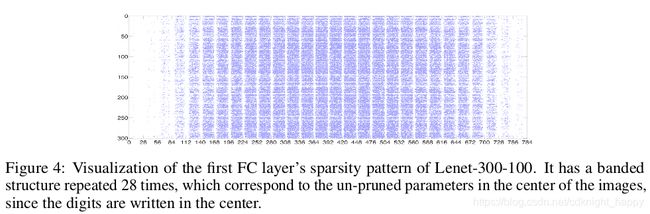上图可以看出，剪枝还产生了类似于attention的效果。对于大小输入为28 * 28的MNIST图像，数字都是写在图像的中间位置的，剪枝后发现图像中间区域对应保留的权重系数更多，边缘区域对应保留的权重更少，说明剪枝后使得网络更加关注有意义的输入区域，起到了attention的效果。

AlexNet和VGG：

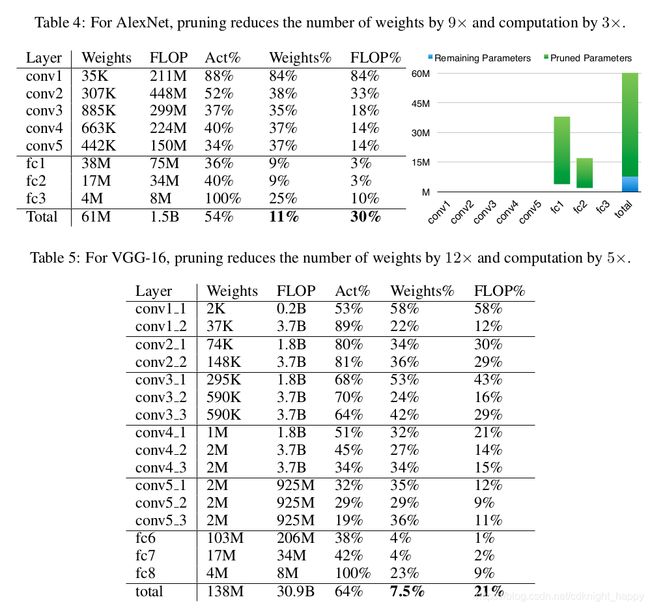
对于不同层的剪枝效果：
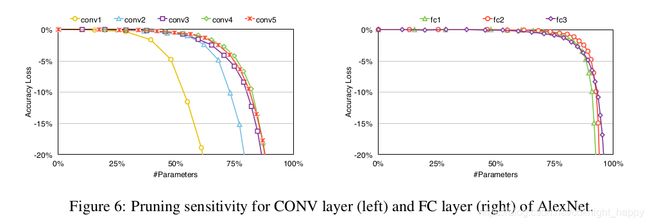相比于fc层，conv层对于剪枝更加敏感。也就对应了上面的实验，fc层可剪的参数更多。

对比其他方法：
剪枝前后参数的分布变化：

剪枝前后，参数的分布发生了变化，幅值也变小了($10^5$ -> $10^4$)。

3 结论

作者提出的三步剪枝思路，在CNN模型上验证了有效性，大幅减少模型参数量和计算量的同时保持了模型的精度。

作者实现的是一个非结构化剪枝，对于CPU、GPU，需要进行专门的优化进行稀疏运算才能真正提速，因为即便某个连接的参数为0默认也是要进行存储和计算的。

4 代码

剪枝的过程，就是将小于指定阈值的参数设为0，阈值的计算参考下面的函数：

def expand_model(model, layers=torch.Tensor()):
    for layer in model.children():
         if len(list(layer.children())) > 0:
             layers = expand_model(layer, layers)
         else:
             if isinstance(layer, nn.Conv2d) and 'mask' not in layer._get_name():
                 layers = torch.cat((layers.view(-1), layer.weight.view(-1)))
    return layers
    
def calculate_threshold(model, rate):
    empty = torch.Tensor()
    if torch.cuda.is_available():
        empty = empty.cuda()
    pre_abs = expand_model(model, empty)
    weights = torch.abs(pre_abs)

    return np.percentile(weights.detach().cpu().numpy(), rate)

def sparsify(model, prune_rate=50.):
    threshold = calculate_threshold(model, prune_rate)
    try:
        model.__prune__(threshold)
    except:
        model.module.__prune__(threshold)
    return model

def __prune__(self, threshold):
        self.mode = 'prune'
        self.mask1.weight.data = torch.mul(torch.gt(torch.abs(self.conv1.weight), threshold).float(), self.mask1.weight)
        layers = [self.block1, self.block2, self.block3]
        for layer in layers:
            for sub_block in layer:
                sub_block.__prune__(threshold)

也就是将模型中参数取绝对值，然后求其指定的百分位(np.percentile函数)，保留大于该阈值的权重。

每次进行模型剪枝后，重新进行模型训练，统计其准确率。在准确率和原始模型一致时尽可能的加大剪枝比例。

剪枝后，只是将被剪掉的连接的参数置为0，理论上说模型的大小和推理速度应该是一致的。因为pytorch Tensor是稠密矩阵，只能整体保存，不能单独保存某几个元素的值。如果想要真正实现模型压缩，需要考虑稀疏矩阵（参考torch.sparse）或者其他的方法。