WanderingSIN
WanderingSIN

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现

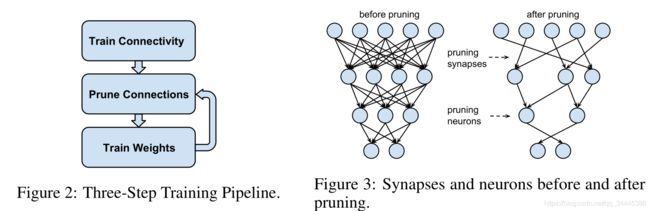
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第1张图片
这是论文中主要的步骤，因此我们复现的时候也主要是利用这个思想。
代码编写需要两个主要部分，首先原来神经网络的训练，然后就是神经网络的裁剪。我这次实验主要是使用论文中说的Lenet-300-100网络来进行测试。

网络的定义以及初次训练

##############先导入需要的包###############################
import torch
import torch.nn as nn
from torchvision import datasets, transforms
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import torch.nn.functional as F
##############导入手写数字体数据###############################
batch_size  = 128
mnist_data = datasets.MNIST('./mnist_data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                   ]))
dataloader = torch.utils.data.DataLoader(dataset=mnist_data,
                                         batch_size=batch_size,
                                         shuffle=True,num_workers = 20)
##############显示手写数字体数据###############################
for i in range(10):
    plt.figure()
    plt.imshow(next(iter(dataloader))[0][0][0],cmap="gray")
##############定义网络Lenet-300-100网络###############################
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(28*28, 300)
        self.fc2 = nn.Linear(300, 100)
        self.fc3 = nn.Linear(100, 10)
    def forward(self, x):
        x = x.view(-1,28*28)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        
        return F.log_softmax(x, dim=1)
def train(model, device, train_loader, optimizer, epoch, log_interval=100):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        
        loss = F.nll_loss(output, target)
       
        loss.backward()
        optimizer.step()
        if batch_idx % log_interval == 0:
            print("Train Epoch: {} [{}/{} ({:0f}%)]\tLoss: {:.6f}".format(
                epoch, batch_idx * len(data), len(train_loader.dataset), 
                100. * batch_idx / len(train_loader), loss.item()
            ))
def test(model, device, test_loader):
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
            pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
            correct += pred.eq(target.view_as(pred)).sum().item()
    test_loss /= len(test_loader.dataset)

    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))
##############初次训练###############################
lr = 0.01
momentum = 0.25
torch.manual_seed(53113)
batch_size = test_batch_size = 128
kwargs = {'num_workers': 40, 'pin_memory': True} if use_cuda else {}
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./mnist_data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./mnist_data', train=False, transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=test_batch_size, shuffle=True, **kwargs)

model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=momentum)
epochs = 20
for epoch in range(1, epochs + 1):
    train(model, device, train_loader, optimizer, epoch)
    test(model, device, test_loader)

训练好网络信息的显示

#####################获取一张图像信息#################################
image = next(iter(dataloader))[0][0][0]
output = model.forward(image)
pred = output.argmax(dim=1, keepdim=True)
print(pred)  #预测值
#####################显示这张图像#################################
plt.figure()
plt.imshow(image,cmap="gray")
plt.show()
#####################图像预处理#################################
image = image.reshape(-1,28*28)
image = image.data.numpy()
image_count = image.copy()
#####################计算图像非零点个数#################################
image_count[image_count != 0] = 1
count = np.sum(image_count)
print(count)
#####################转化到numpy对数据进行处理#################################
fc1 = model.fc1.weight.data.cpu().numpy()
fc2 = model.fc2.weight.data.cpu().numpy()
fc3 = model.fc3.weight.data.cpu().numpy()
hidden1 = image.dot(fc1.T) 
hidden1 = np.maximum(0, hidden1)   #激活
hidden2 = hidden1.dot(fc2.T)
hidden2 = np.maximum(0, hidden2)
hidden3 = hidden2.dot(fc3.T)
#####################第一层神经元激活的个数#################################
hidden1_count = hidden1.copy()
hidden1_count[hidden1_count > 0] = 1
count = np.sum(hidden1_count)
print(count)
#####################第二层神经元激活的个数#################################
hidden2_count = hidden2.copy()
hidden2_count[hidden2_count > 0] = 1
count = np.sum(hidden2_count)
print(count)
#####################输出预测结果#################################
out = np.exp(hidden3)
out = out / np.sum(out)
print(np.argmax(out))
#####################第一层神经元参数信息的图像深度显示，从这里可以观测出权重的变化#################################
fc1_plt =  np.abs(fc1)
print("min",np.min(fc1_plt),"max",np.max(fc1_plt))
plt.figure(figsize=(50,50))
im = plt.imshow(fc1_plt, vmin = np.min(fc1_plt), vmax =  np.max(fc1_plt) ,cmap = 'seismic')
plt.show()

剪枝操作

##########################函数定义###########################################
def expand_model(model, layers=torch.Tensor()):
    for layer in model.children():
         layers = torch.cat((layers.view(-1), layer.weight.view(-1)))  #将所有的参数拼接在一起
    return layers

def calculate_threshold(model, rate):   #求取所有参数的阈值所在的数值大小
    empty = torch.Tensor()
    if torch.cuda.is_available():
        empty = empty.cuda()
    pre_abs = expand_model(model, empty)    #获取所有的参数为一行
    weights = torch.abs(pre_abs)            #求绝对值

    return np.percentile(weights.detach().cpu().numpy(), rate)
def prune(model, threshold):
    model.fc1.weight.data = torch.mul(torch.gt(torch.abs(model.fc1.weight.data), threshold), model.fc1.weight.data)
    model.fc2.weight.data = torch.mul(torch.gt(torch.abs(model.fc2.weight.data), threshold), model.fc2.weight.data)
    model.fc3.weight.data = torch.mul(torch.gt(torch.abs(model.fc3.weight.data), threshold), model.fc3.weight.data)
def retrain(model, device, train_loader, test_loader, epochs, lr, momentum):
    optimizer = optim.SGD(model.parameters(), lr=lr, momentum=momentum)
    for epoch in range(1, epochs + 1):
        train(model, device, train_loader, optimizer, epoch)
        test(model, device, test_loader)
##########################按百分比计算剪枝的阈值###########################################
threshold = calculate_threshold(model, 96)
print(threshold)
##########################进行剪枝操作并计算测试正确率###########################################
prune(model, threshold)
test(model, device, test_loader)
##########################剪枝操作后进行再次训练###########################################
retrain(model, device, train_loader ,test_loader, 20, 0.001, 0.25)

权重柱状图绘制

# 提取绘制的数据
def paraCount(layers, location, index):
    values = []
    for value in layers:
        if location[index] == 0:
            values.append(value)
        index += 1
    values = np.array(values)
    return  values
###########################绘制剪枝后的整体参数分布############################
layers = expand_model(model)   
layers = layers.detach().cpu().numpy()
values = paraCount(layers, location, 0)
plt.figure(figsize=(20,5))
plt.hist(values, bins = 1000)
plt.show()
###########################绘制第一层网络参数分布############################
fc1_hist = fc1.reshape(-1)
fc1_hist = paraCount(fc1_hist, location, 0)
plt.figure(figsize=(20,5))
plt.hist(fc1_hist, bins = 300)
plt.show()
###########################绘制第二层网络参数分布############################
fc2_hist = fc2.reshape(-1)
fc2_hist = paraCount(fc2_hist, location, fc1.shape[0] * fc1.shape[1])
plt.figure(figsize=(20,5))
plt.hist(fc2_hist, bins = 100)
plt.show()
###########################绘制第三层网络参数分布############################
fc3_hist = fc3.reshape(-1)
fc3_hist = paraCount(fc3_hist,location, fc1.shape[0] * fc1.shape[1] + fc2.shape[0] * fc2.shape[1])
plt.figure(figsize=(20,5))
plt.hist(fc3_hist, bins = 100)
plt.show()

这个剪枝操作需要重复进行，这个全连接的神经网络，我可以剪枝掉98%后，正确率还是会有90%，而且经过多次剪枝操作后，网络大部分的参数接近与零，只有重要的参数才会起作用。
jupyter下实现的代码，需要的可以去下载: link.

实验

下面就是基于以上的代码，使用手写数字体的数据集进行的实验，我会记录实验过程中的数据变化过程。

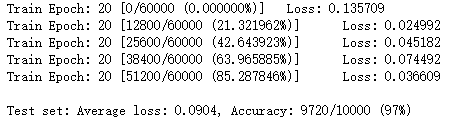
初次训练网络

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第2张图片

神经元激活

从上图可以看出，经过20次的迭代，网络的正确率已经到达了97%
对于数字4的图像进行识别，图像的非零点数是75个，第一层神经元激活个数169，第二层神经元激活个数70，识别结果是4正确

层数 个数
fc1 169
fc2 70
fc3 结果是4

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第3张图片

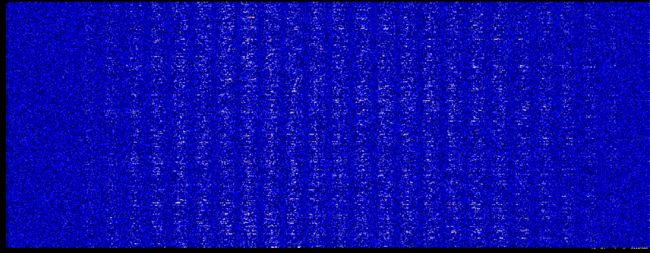
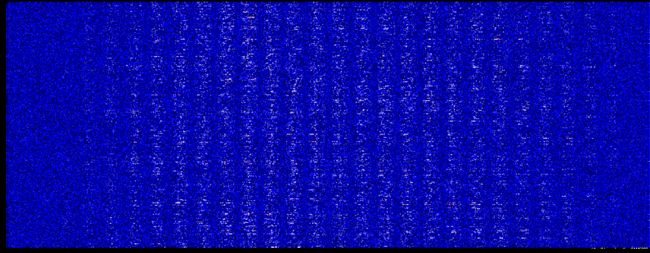
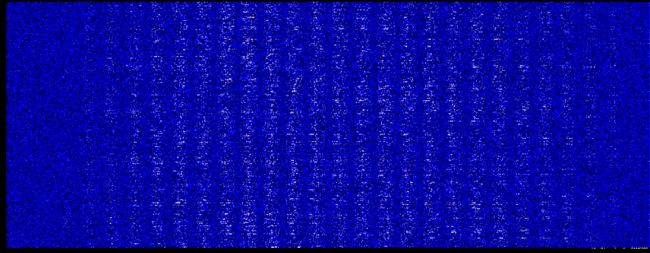
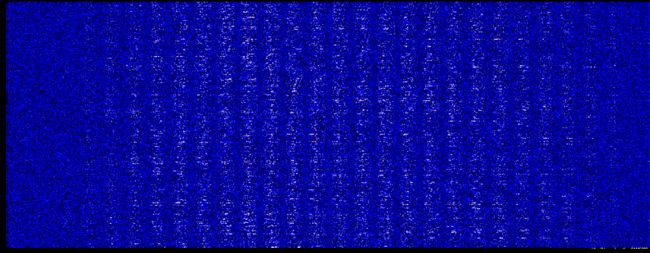
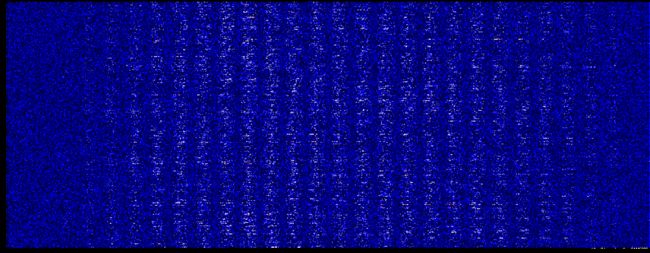
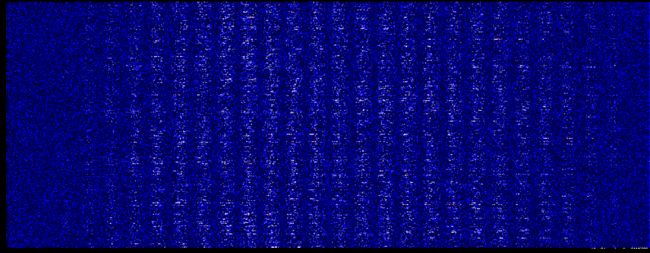
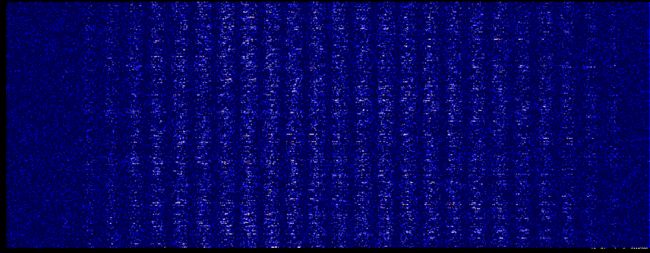
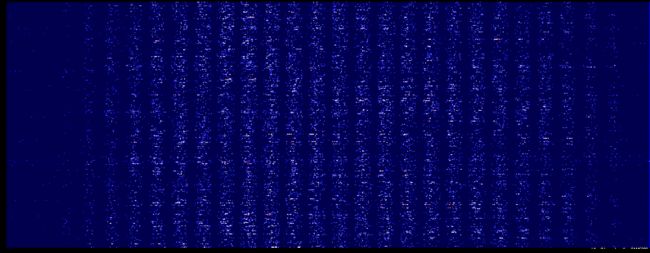
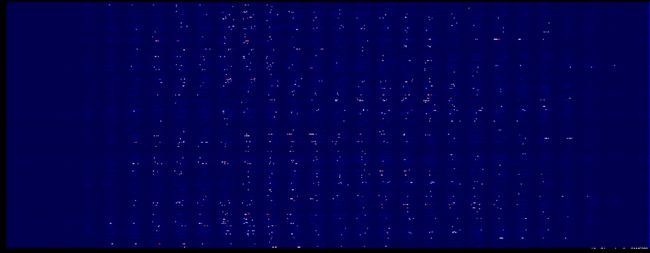
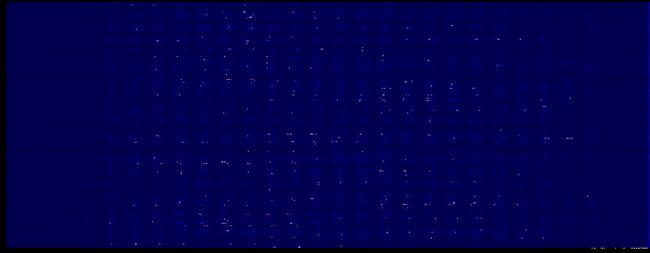
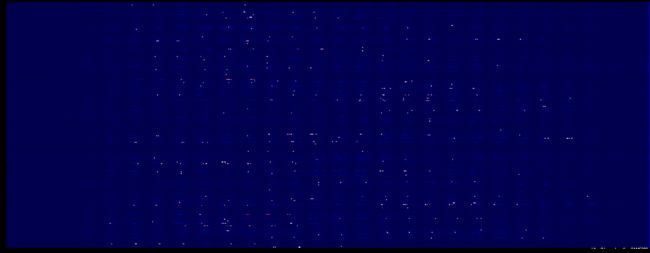
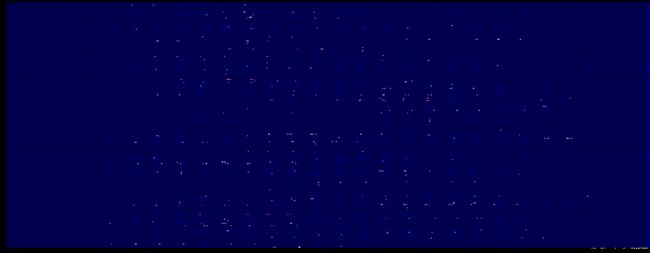
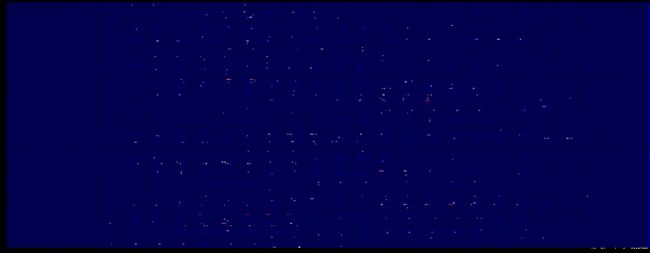
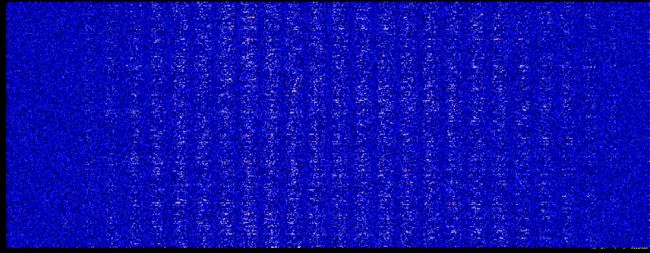
第一层权重的深度分布图

下面是初次训练第一层权重的深度分布图，从这里可以明显的看到了28的分割轮廓了，两端的参数较小，不太重要。
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第4张图片

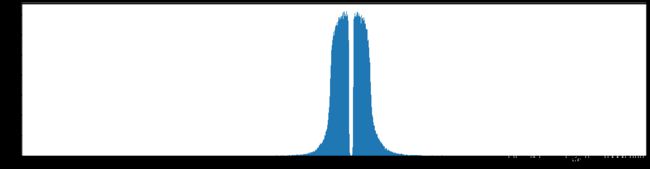
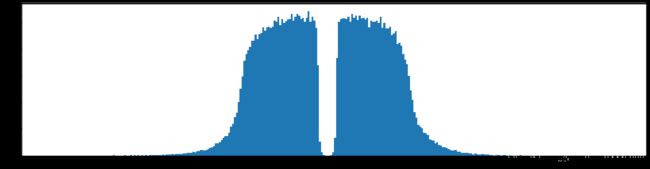
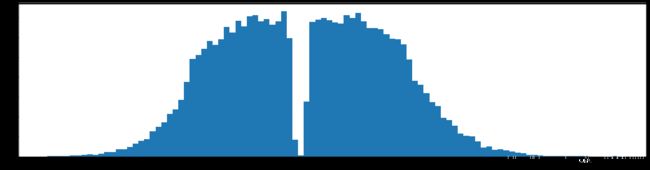
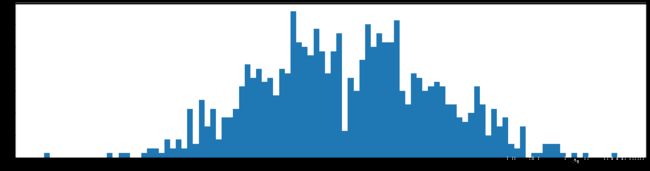
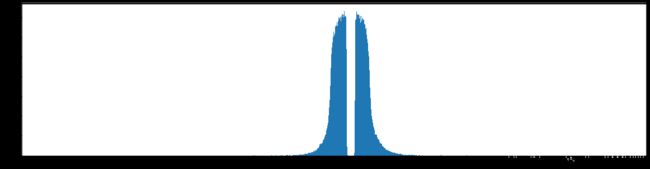
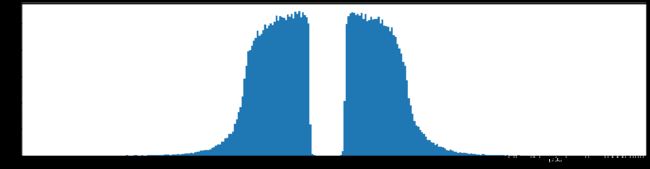
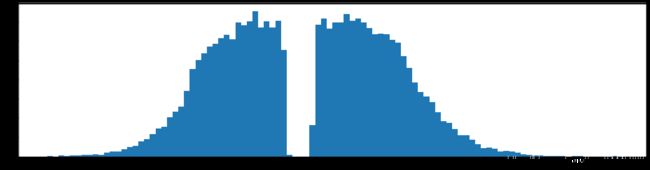
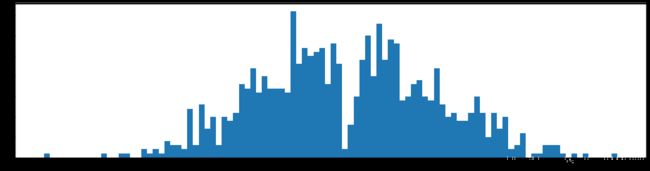
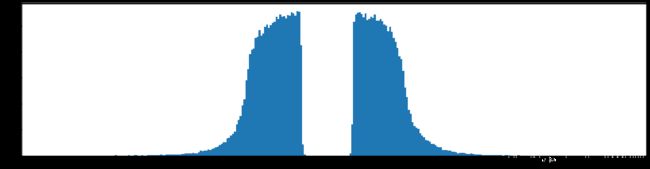
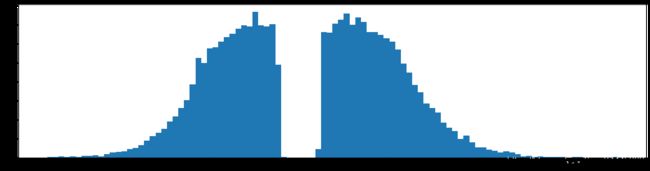
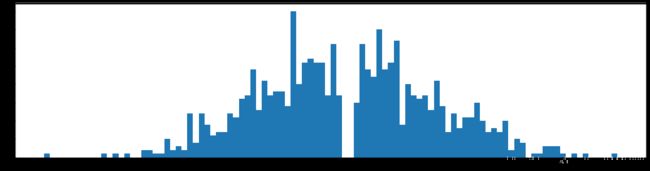
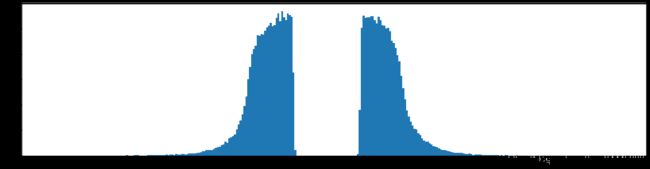
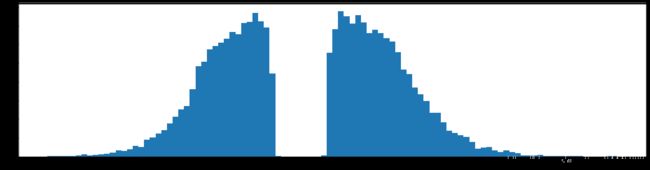
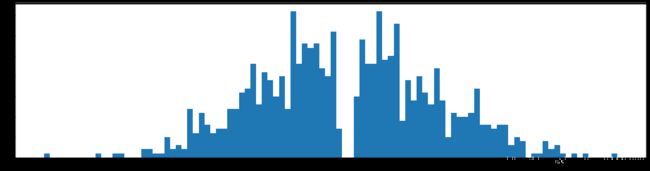
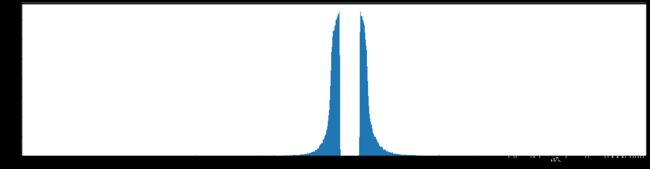
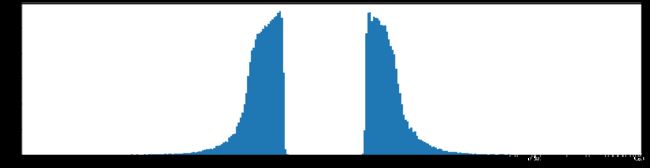
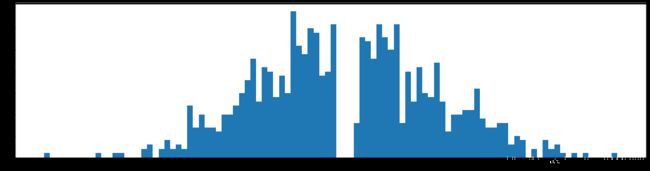
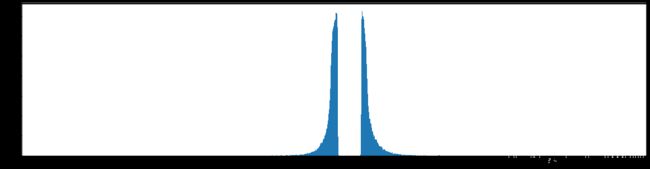
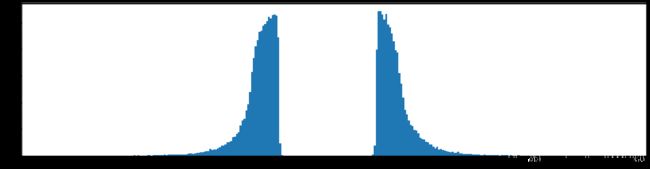
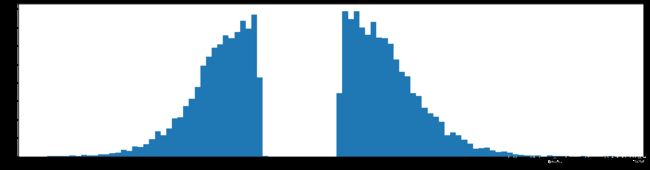
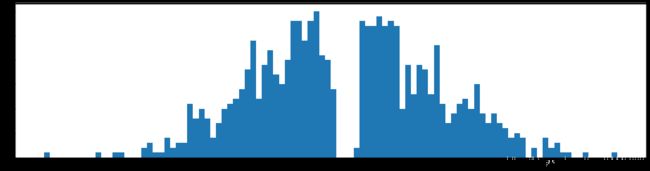
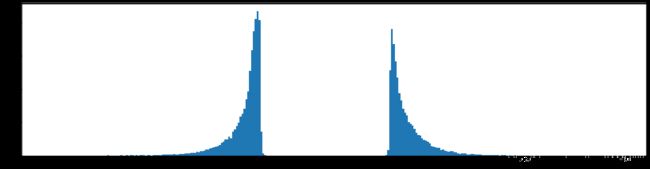
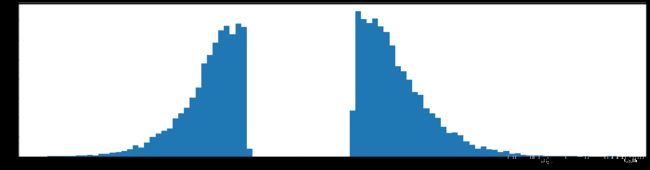
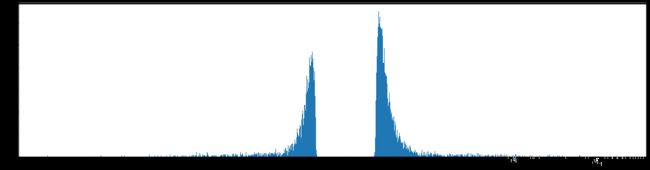
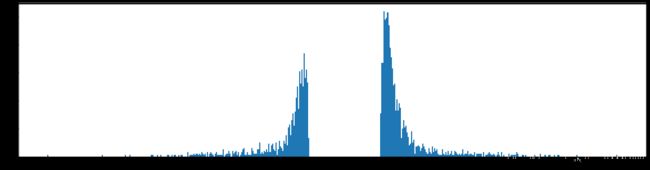
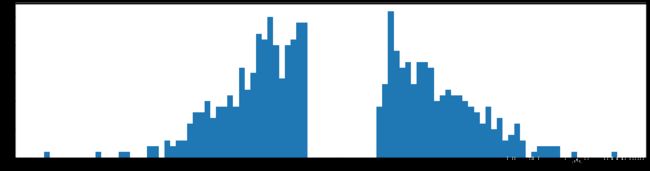
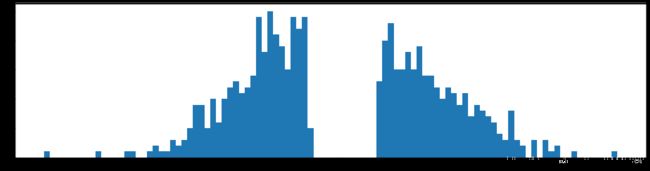
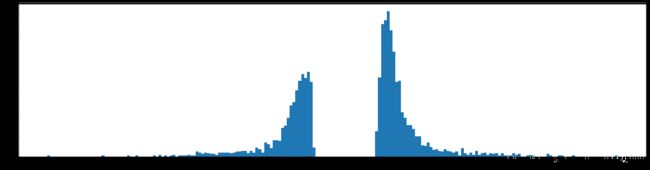
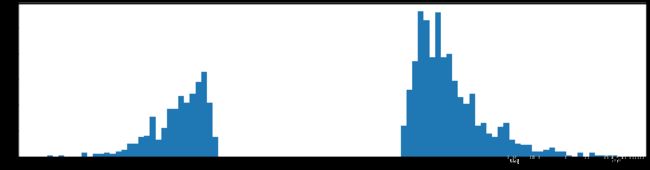
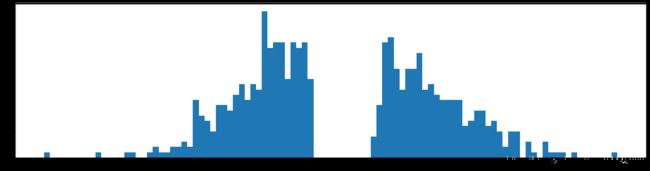
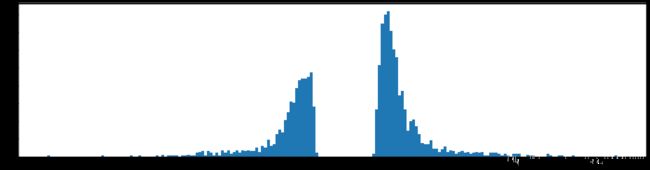
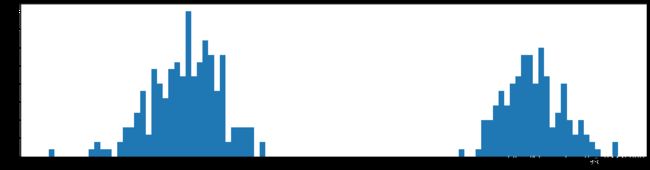
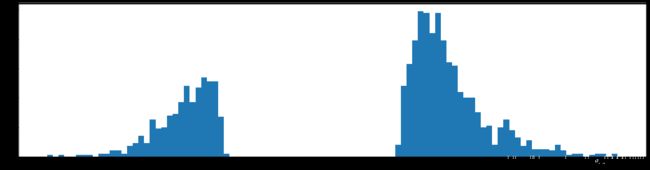
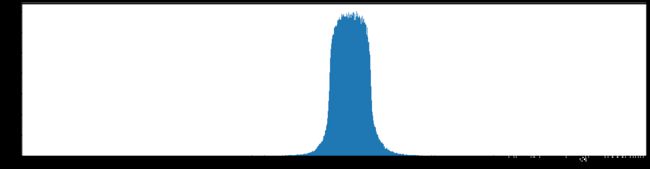
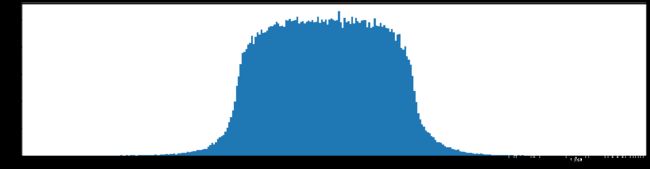
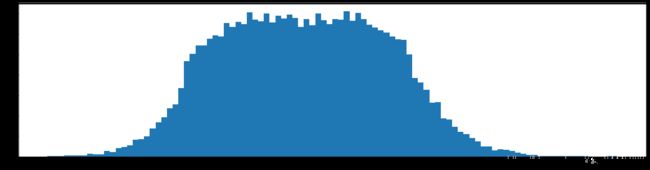
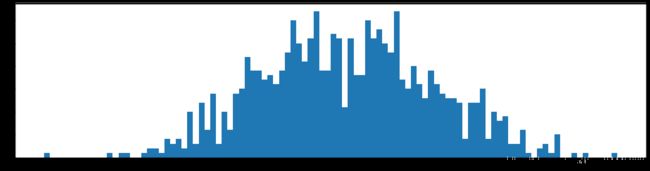
权重柱状图

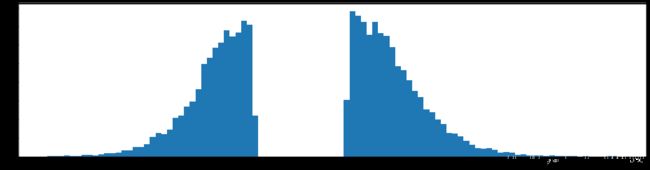
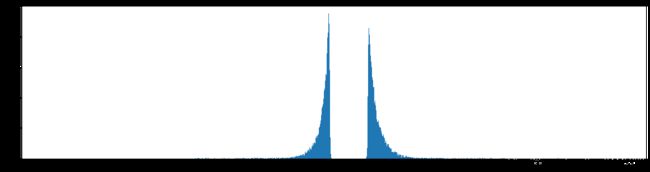
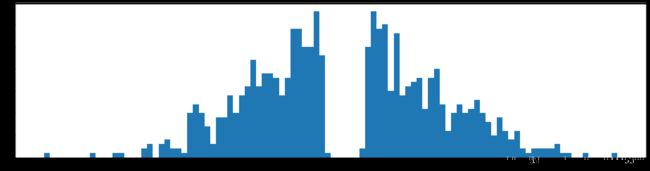
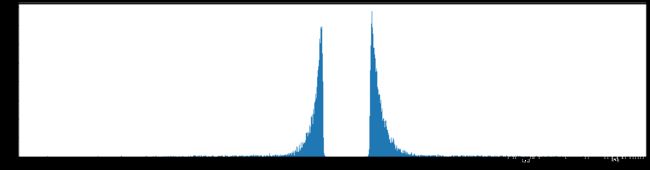
下图是全部参数的柱状图、第一层参数的柱状图、第二层参数的柱状图、第三层参数的柱状图，可以看出参数都基本集中的0附近，成中心分布的样子。
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第5张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第6张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第7张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第8张图片

剪枝10%参数

计算出来的阈值是：0.0038155303103849293
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第9张图片
比初次训练的正确个数还多了，说不定这个可以增加泛化能力。

神经元激活

层数 个数
fc1 167
fc2 71
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，亮的地方变的更亮了一点。
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第10张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第11张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第12张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第13张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第14张图片

剪枝20%参数

计算出来的阈值是：0.007650174759328366
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
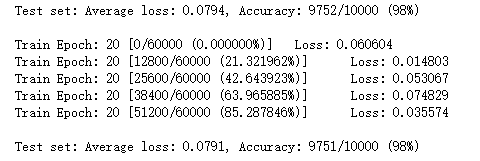
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第15张图片
比上训练的正确个数还多了，又增加泛化能力。

神经元激活

层数 个数
fc1 172
fc2 73
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方增多了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第16张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第17张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第18张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第19张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第20张图片

剪枝30%参数

计算出来的阈值是：0.01150485947728157
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第21张图片
比上训练的正确个数还多了，又增加泛化能力。

神经元激活

层数 个数
fc1 169
fc2 74
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第22张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第23张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第24张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第25张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第26张图片

剪枝40%参数

计算出来的阈值是：0.01536105088889599
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第27张图片
比上训练的正确个数还多了，又增加泛化能力。

神经元激活

层数 个数
fc1 167
fc2 73
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第28张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第29张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第30张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第31张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第32张图片

剪枝50%参数

计算出来的阈值是：0.019335072487592697
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第33张图片
比上训练的正确个数还多了，又增加泛化能力。

神经元激活

层数 个数
fc1 171
fc2 73
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第34张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第35张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第36张图片在这里插入图片描述
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第37张图片

剪枝60%参数

计算出来的阈值是：0.023352954909205435
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第38张图片
比上训练的正确个数还多了，又增加泛化能力。

神经元激活

层数 个数
fc1 176
fc2 74
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第39张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第40张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第41张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第42张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第43张图片

剪枝70%参数

计算出来的阈值是：0.02758437413722277
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第44张图片
比上训练的正确个数还多了，又增加泛化能力。

神经元激活

层数 个数
fc1 174
fc2 73
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第45张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第46张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第47张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第48张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第49张图片

剪枝80%参数

计算出来的阈值是：0.03225095123052597
在这里插入图片描述
剪枝后的正确率并没有明显的变化，仍旧是97%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第50张图片
和上次训练的正确个数差不多，网络性能没有增加了

神经元激活

层数 个数
fc1 181
fc2 77
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第51张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第52张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第53张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第54张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第55张图片

剪枝90%参数

计算出来的阈值是：0.039930999279022224
在这里插入图片描述
剪枝后的正确率发生了变化，下降到了93%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第56张图片
和上次训练的正确个数差不多，网络性能没有增加了

神经元激活

层数 个数
fc1 184
fc2 78
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第57张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第58张图片在这里插入图片描述Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第59张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第60张图片

剪枝95%参数

计算出来的阈值是：0.05171532221138477
在这里插入图片描述
剪枝后的正确率发生了变化，下降到了85%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第61张图片
和上次训练的正确个数差不多，网络性能没有增加了

神经元激活

层数 个数
fc1 189
fc2 84
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第62张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第63张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第64张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第65张图片
在这里插入图片描述

剪枝98%参数

计算出来的阈值是：0.07121909260749816
在这里插入图片描述
剪枝后的正确率降到了很低，下降到了60%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第66张图片
和上次训练的正确个数差不多，网络性还是能够恢复的

神经元激活

层数 个数
fc1 174
fc2 76
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第67张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第68张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第69张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第70张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第71张图片

剪枝99%参数

计算出来的阈值是：0.091620362251997
在这里插入图片描述
剪枝后的正确率降到了很低，下降到了46%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第72张图片
和上次训练的正确个数下降一个百分点，网络性还是能够恢复的，但是恢复的性能略有下降

神经元激活

层数 个数
fc1 169
fc2 74
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第73张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第74张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第75张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第76张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第77张图片

剪枝99%参数

计算出来的阈值是：0.04240277148829452
在这里插入图片描述
剪枝后的正确率降到了很低，下降到了50%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第78张图片
和上次训练的正确个数下降一个百分点，网络性还是能够恢复的，但是恢复的性能略有下降

神经元激活

层数 个数
fc1 167
fc2 75
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第79张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第80张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第81张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第82张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第83张图片

剪枝99%参数

计算出来的阈值是：0.04132488820748184
在这里插入图片描述
剪枝后的正确率降到了很低，下降到了50%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第84张图片
和上次训练的正确个数下降一个百分点，网络性还是能够恢复的，但是恢复的性能略有下降

神经元激活

层数 个数
fc1 167
fc2 77
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第85张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第86张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第87张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第88张图片
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第89张图片

剪枝99%参数

计算出来的阈值是：0.04077488094611925
在这里插入图片描述
剪枝后的正确率降到了很低，下降到了50%
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第90张图片
和上次训练的正确个数下降一个百分点，网络性还是能够恢复的，但是恢复的性能略有下降

神经元激活

层数 个数
fc1 167
fc2 77
fc3 结果是4

第一层权重的深度分布图

仔细对比可以发现，这次好像图像暗的地方更暗了
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第91张图片

权重柱状图

Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第92张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第93张图片Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第94张图片
在这里插入图片描述

剪枝99%参数

经过非常多次剪枝99%然后参数再训练，整个网络的性能还是会慢慢提升的
计算出来的阈值是：0.025321735092738397
在这里插入图片描述
剪枝后的正确率降到了很低，下降到了65%，但是比刚开始还是有明显的提高
然后进行再训练
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第95张图片
和上次训练的正确个数下降一个百分点，网络性还是能够恢复的，还是快恢复到了巅峰时期
然后剪枝80%
计算出来的阈值是：0.0012542949290946129
在这里插入图片描述

层数 个数
fc1 124
fc2 69
fc3 结果是4

然后剪枝90%
计算出来的阈值是：0.0027993932599201803
在这里插入图片描述

层数 个数
fc1 101
fc2 66
fc3 结果是4

然后剪枝95%
计算出来的阈值是：0.005025399965234099
在这里插入图片描述

层数 个数
fc1 78
fc2 64
fc3 结果是4

然后剪枝99%
计算出来的阈值是：0.02462294178083847
在这里插入图片描述

层数 个数
fc1 25
fc2 56
fc3 结果是1

通过上面的一系列数据，其实可以发现，网络中90的参数可以删掉，几乎不会影响准确性。95%的删掉，准确性还是可以接受。但是相对于参数的减少，在实际运算过程中，激活神经元的减少数量其实没有那么明显，当删除95% 的参数时，才会减少一半左右的神经元，当删除99%的参数时，神经元能够大幅度减少，但是可以发现现在的预测准确性已经无法接受。
同时，也可以发现，当前可以删除的神经元是在第一层全连接层，而第二层全连接层明显变化没有第一层剧烈。
思考：
神经网络的结构是每递进一层深度，所获得的信息就会更加抽象，说明在深层处抽象的特征多余的较少。

第一层权重的深度分布图

仔细对比可以发现，图片里面亮起来的点已经非常少了，基本上就是亮的和不亮的了。
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第96张图片

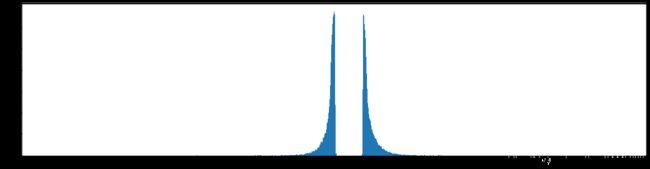
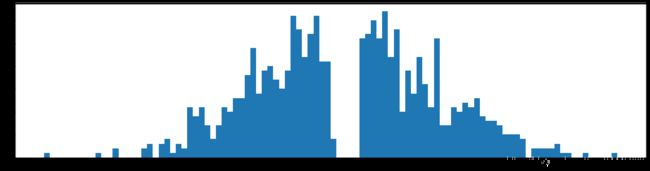
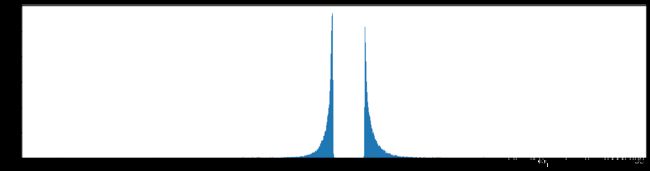
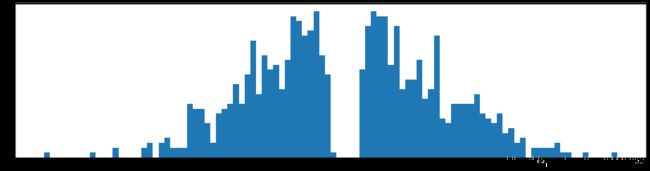
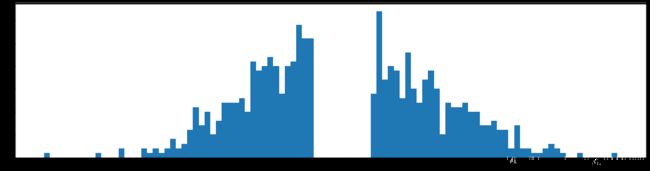
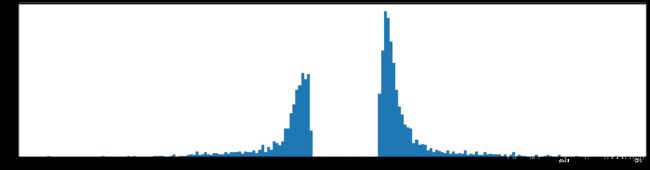
权重柱状图

99%裁剪的情况下，一共使用了2662参数。
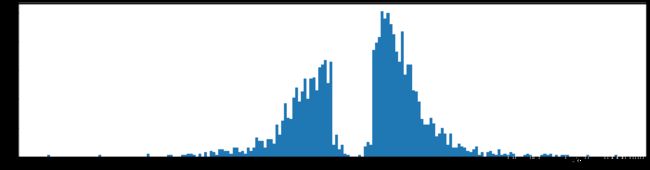
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第97张图片
第一层一共使用了379个参数，此时和刚开始2828300=235200，减少了620倍，在浅层的多余参数这么多的嘛。而且，也可以看到，参数大量集中到了0.2左右的中心分布，偏离了原来以0为中心分布的情况。

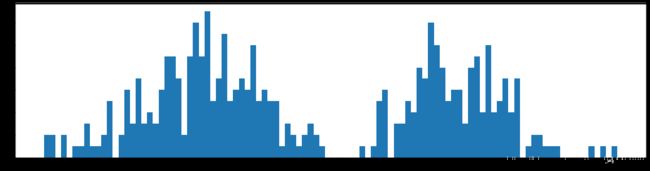
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第98张图片
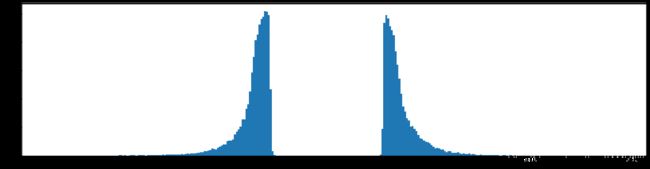
第二层一共使用了1654个参数，此时和刚开始100*300=30000，减少了18倍。参数几乎还是以零为中心在分布。
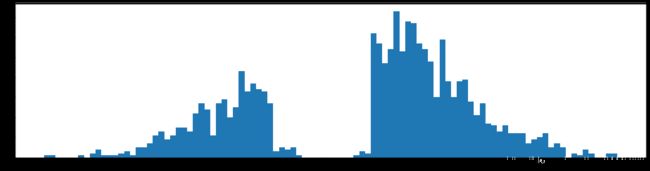
Learning both Weights and Connections for Efficient Neural Networks 论文pytorch复现_第99张图片

第三层一共使用了629个参数，此时和刚开始100*10=1000，减少了1.59倍。可见参数其实减少的非常少。
在这里插入图片描述

思考与提问

从上面的分析，可以发现，越深层的参数和神经元越重要，从参数的大小和被裁剪的多少都可以明显的看出。这里我们是按照所有层的参数放在一起按百分比进行裁剪，如果是按照每一层自己的百分比进行裁剪，是不是整个训练精度就会下降很多，明显不如这一个？下面可以做一个实验测试一下。
还有就是，现在我们第一层的神经元是300个，底层每次要激活170个左右，大概是在50%的激活率，如果我们把第一层的神经元个数增加到600个，那么每次激活的个数还是50%左右还是170吗？，如果我们进行同样的剪枝操作之后激活的个数或者百分比有什么变化？

你可能感兴趣的:(神经网络,Python,神经网络,深度学习,剪枝)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • Python数据分析与可视化实战指南 William数据分析 pythonpython数据
    在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
  • python os.environ 江湖偌大 python深度学习
    os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
  • Python中os.environ基本介绍及使用方法 鹤冲天Pro #Pythonpython服务器开发语言
    文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
  • Pyecharts数据可视化大屏：打造沉浸式数据分析体验 我的运维人生 信息可视化数据分析数据挖掘运维开发技术共享
    Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
  • Python教程：一文了解使用Python处理XPath 旦莫 Python进阶python开发语言
    目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
  • python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 pythonos.environ
    >>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
  • 将cmd中命令输出保存为txt文本文件 落难Coder Windowscmdwindow
    最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
  • 使用Faiss进行高效相似度搜索 llzwxh888 faisspython
    在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
  • python是什么意思中文-在python中%是什么意思 编程大乐趣
    Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
  • Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Pythonpython开发语言大数据数据分析数据挖掘
    大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
  • python八股文面试题分享及解析(1) Shawn________ python
    #1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • Python快速入门 —— 第三节：类与对象 孤华暗香 Python快速入门python开发语言
    第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
  • pyecharts——绘制柱形图折线图 2224070247 信息可视化pythonjava数据可视化
    一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
  • Python 实现图片裁剪（附代码） | Python工具 剑客阿良_ALiang
    前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
  • 【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师 华为od面试python
    华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
  • python os 环境变量 CV矿工 python开发语言numpy
    环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
  • Python爬虫解析工具之xpath使用详解 eqa11 python爬虫开发语言
    文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
  • 【华为OD技术面试真题 - 技术面】- python八股文真题题库（1） 算法大师 华为od面试python
    华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
  • nosql数据库技术与应用知识点 皆过客，揽星河 NoSQLnosql数据库大数据数据分析数据结构非关系型数据库
    Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
  • 《Python数据分析实战终极指南》 xjt921122 python数据分析开发语言
    对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
  • Python中深拷贝与浅拷贝的区别 yuxiaoyu.
    转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • Python编译器 鹿鹿~ Python编译器Pythonpython开发语言后端
    嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
  • 一文掌握python面向对象魔术方法（二） 程序员neil pythonpython开发语言
    接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
  • 一文掌握python常用的list（列表）操作 程序员neil pythonpython开发语言
    目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
  • Python实现简单的机器学习算法 master_chenchengg pythonpython办公效率python开发IT
    Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
  • python中的深拷贝与浅拷贝 anshejd70787 python
    深拷贝和浅拷贝浅拷贝的时候，修改原来的对象，浅拷贝的对象不会发生改变。1、对象的赋值对象的赋值实际上是对象之间的引用：当创建一个对象，然后将这个对象赋值给另外一个变量的时候，python并没有拷贝这个对象，而只是拷贝了这个对象的引用。当对对象做赋值或者是参数传递或者作为返回值的时候，总是传递原始对象的引用，而不是一个副本。如下所示：>>>aList=["kel","abc",123]>>>bLis
  • iOS http封装 374016526 ios服务器交互http网络请求
    程序开发避免不了与服务器的交互，这里打包了一个自己写的http交互库。希望可以帮到大家。   内置一个basehttp，当我们创建自己的service可以继承实现。   KuroAppBaseHttp *baseHttp = [[KuroAppBaseHttp alloc] init]; [baseHttp setDelegate:self]; [baseHttp
  • lolcat ：一个在 Linux 终端中输出彩虹特效的命令行工具 brotherlamp linuxlinux教程linux视频linux自学linux资料
      那些相信 Linux 命令行是单调无聊且没有任何乐趣的人们，你们错了，这里有一些有关 Linux 的文章，它们展示着 Linux 是如何的有趣和“淘气” 。 在本文中，我将讨论一个名为“lolcat”的小工具 – 它可以在终端中生成彩虹般的颜色。 何为 lolcat ? Lolcat 是一个针对 Linux，BSD 和 OSX 平台的工具，它类似于 cat 命令，并为 cat
  • MongoDB索引管理（1）——[九] eksliang mongodbMongoDB管理索引
    转载请出自出处：http://eksliang.iteye.com/blog/2178427 一、概述       数据库的索引与书籍的索引类似，有了索引就不需要翻转整本书。数据库的索引跟这个原理一样，首先在索引中找，在索引中找到条目以后，就可以直接跳转到目标文档的位置，从而使查询速度提高几个数据量级。       不使用索引的查询称
  • Informatica参数及变量 18289753290 Informatica参数变量
    下面是本人通俗的理解，如有不对之处，希望指正 info参数的设置：在info中用到的参数都在server的专门的配置文件中（最好以parma）结尾 下面的GLOBAl就是全局的，$开头的是系统级变量，$$开头的变量是自定义变量。如果是在session中或者mapping中用到的变量就是局部变量，那就把global换成对应的session或者mapping名字。 [GLOBAL] $Par
  • python 解析unicode字符串为utf8编码字符串 酷的飞上天空 unicode
    php返回的json字符串如果包含中文，则会被转换成\uxx格式的unicode编码字符串返回。 在浏览器中能正常识别这种编码，但是后台程序却不能识别，直接输出显示的是\uxx的字符，并未进行转码。   转换方式如下   >>> import json >>> q = '{"text":"\u4
  • Hibernate的总结 永夜-极光 Hibernate
    1.hibernate的作用,简化对数据库的编码,使开发人员不必再与复杂的sql语句打交道   做项目大部分都需要用JAVA来链接数据库，比如你要做一个会员注册的 页面，那么 获取到用户填写的 基本信后，你要把这些基本信息存入数据库对应的表中，不用hibernate还有mybatis之类的框架，都不用的话就得用JDBC，也就是JAVA自己的，用这个东西你要写很多的代码，比如保存注册信
  • SyntaxError: Non-UTF-8 code starting with '\xc4' 随便小屋 python
    刚开始看一下Python语言，传说听强大的，但我感觉还是没Java强吧！ 写Hello World的时候就遇到一个问题，在Eclipse中写的，代码如下 ''' Created on 2014年10月27日 @author: Logic ''' print("Hello World!");  运行结果 SyntaxError: Non-UTF-8
  • 学会敬酒礼仪 不做酒席菜鸟 aijuans 菜鸟
    俗话说，酒是越喝越厚，但在酒桌上也有很多学问讲究，以下总结了一些酒桌上的你不得不注意的小细节。 细节一：领导相互喝完才轮到自己敬酒。敬酒一定要站起来，双手举杯。 细节二：可以多人敬一人，决不可一人敬多人，除非你是领导。 细节三：自己敬别人，如果不碰杯，自己喝多少可视乎情况而定，比如对方酒量，对方喝酒态度，切不可比对方喝得少，要知道是自己敬人。 细节四：自己敬别人，如果碰杯，一
  • 《创新者的基因》读书笔记 aoyouzi 读书笔记《创新者的基因》
    创新者的基因   创新者的“基因”，即最具创意的企业家具备的五种“发现技能”：联想，观察，实验，发问，建立人脉。   第一部分破坏性创新，从你开始 第一章破坏性创新者的基因 如何获得启示： 发现以下的因素起到了催化剂的作用：(1) -个挑战现状的问题；(2)对某项技术、某个公司或顾客的观察；(3) -次尝试新鲜事物的经验或实验；(4)与某人进行了一次交谈，为他点醒
  • 表单验证技术 百合不是茶 JavaScriptDOM对象String对象事件
    js最主要的功能就是验证表单,下面是我对表单验证的一些理解,贴出来与大家交流交流  ,数显我们要知道表单验证需要的技术点, String对象,事件,函数   一:String对象;通常是对字符串的操作;   1,String的属性;   字符串.length;表示该字符串的长度; var str= "java"
  • web.xml配置详解之context-param bijian1013 javaservletweb.xmlcontext-param
    一.格式定义： <context-param> <param-name>contextConfigLocation</param-name> <param-value>contextConfigLocationValue></param-value> </context-param> 作用：该元
  • Web系统常见编码漏洞（开发工程师知晓） Bill_chen sqlPHPWebfckeditor脚本
    1.头号大敌：SQL Injection 原因：程序中对用户输入检查不严格，用户可以提交一段数据库查询代码，根据程序返回的结果， 获得某些他想得知的数据，这就是所谓的SQL Injection，即SQL注入。 本质: 对于输入检查不充分，导致SQL语句将用户提交的非法数据当作语句的一部分来执行。 示例： String query = "SELECT id FROM users
  • 【MongoDB学习笔记六】MongoDB修改器 bit1129 mongodb
    本文首先介绍下MongoDB的基本的增删改查操作，然后，详细介绍MongoDB提供的修改器，以完成各种各样的文档更新操作  MongoDB的主要操作 show dbs 显示当前用户能看到哪些数据库 use foobar 将数据库切换到foobar show collections 显示当前数据库有哪些集合 db.people.update，update不带参数，可
  • 提高职业素养，做好人生规划 白糖_ 人生
      培训讲师是成都著名的企业培训讲师，他在讲课中提出的一些观点很新颖，在此我收录了一些分享一下。注：讲师的观点不代表本人的观点，这些东西大家自己揣摩。   1、什么是职业规划：职业规划并不完全代表你到什么阶段要当什么官要拿多少钱，这些都只是梦想。职业规划是清楚的认识自己现在缺什么，这个阶段该学习什么，下个阶段缺什么，又应该怎么去规划学习，这样才算是规划。  
  • 国外的网站你都到哪边看？ bozch 技术网站国外
    学习软件开发技术，如果没有什么英文基础，最好还是看国内的一些技术网站，例如：开源OSchina，csdn，iteye,51cto等等。 个人感觉如果英语基础能力不错的话，可以浏览国外的网站来进行软件技术基础的学习，例如java开发中常用的到的网站有apache.org 里面有apache的很多Projects,springframework.org是spring相关的项目网站,还有几个感觉不错的
  • 编程之美-光影切割问题 bylijinnan 编程之美
    package a; public class DisorderCount { /**《编程之美》“光影切割问题” * 主要是两个问题： * 1.数学公式（设定没有三条以上的直线交于同一点）： * 两条直线最多一个交点，将平面分成了4个区域； * 三条直线最多三个交点，将平面分成了7个区域； * 可以推出：N条直线 M个交点，区域数为N+M+1。
  • 关于Web跨站执行脚本概念 chenbowen00 Web安全跨站执行脚本
    跨站脚本攻击(XSS)是web应用程序中最危险和最常见的安全漏洞之一。安全研究人员发现这个漏洞在最受欢迎的网站,包括谷歌、Facebook、亚马逊、PayPal,和许多其他网站。如果你看看bug赏金计划,大多数报告的问题属于 XSS。为了防止跨站脚本攻击,浏览器也有自己的过滤器,但安全研究人员总是想方设法绕过这些过滤器。这个漏洞是通常用于执行cookie窃取、恶意软件传播,会话劫持,恶意重定向。在
  • [开源项目与投资]投资开源项目之前需要统计该项目已有的用户数 comsci 开源项目
            现在国内和国外,特别是美国那边,突然出现很多开源项目,但是这些项目的用户有多少,有多少忠诚的粉丝,对于投资者来讲,完全是一个未知数,那么要投资开源项目,我们投资者必须准确无误的知道该项目的全部情况,包括项目发起人的情况,项目的维持时间..项目的技术水平,项目的参与者的势力,项目投入产出的效益.....
  • oracle alert log file（告警日志文件） daizj oracle告警日志文件alert log file
    The alert log is a chronological log of messages and errors, and includes the following items: All internal errors (ORA-00600), block corruption errors (ORA-01578), and deadlock errors (ORA-00060)
  • 关于 CAS SSO 文章声明 denger SSO
    由于几年前写了几篇 CAS 系列的文章，之后陆续有人参照文章去实现，可都遇到了各种问题，同时经常或多或少的收到不少人的求助。现在这时特此说明几点： 1.  那些文章发表于好几年前了，CAS 已经更新几个很多版本了，由于近年已经没有做该领域方面的事情，所有文章也没有持续更新。 2. 文章只是提供思路，尽管 CAS 版本已经发生变化，但原理和流程仍然一致。最重要的是明白原理，然后
  • 初二上学期难记单词 dcj3sjt126com englishword
    lesson 课 traffic 交通 matter 要紧；事物 happy 快乐的，幸福的 second 第二的 idea 主意；想法；意见 mean 意味着 important 重要的，重大的 never 从来，决不 afraid 害怕 的 fifth 第五的 hometown 故乡，家乡 discuss 讨论；议论 east 东方的 agree 同意；赞成 bo
  • uicollectionview 纯代码布局, 添加头部视图 dcj3sjt126com Collection
    #import <UIKit/UIKit.h> @interface myHeadView : UICollectionReusableView { UILabel *TitleLable; } -(void)setTextTitle; @end #import "myHeadView.h" @implementation m
  • N 位随机数字串的 JAVA 生成实现 FX夜归人 javaMath随机数Random
    /** * 功能描述 随机数工具类<br /> * @author FengXueYeGuiRen * 创建时间 2014-7-25<br /> */ public class RandomUtil { // 随机数生成器 private static java.util.Random random = new java.util.R
  • Ehcache（09）——缓存Web页面 234390216 ehcache页面缓存
    页面缓存 目录 1       SimplePageCachingFilter 1.1      calculateKey 1.2      可配置的初始化参数 1.2.1     cach
  • spring中少用的注解@primary解析 jackyrong primary
    这次看下spring中少见的注解@primary注解，例子 @Component public class MetalSinger implements Singer{ @Override public String sing(String lyrics) { return "I am singing with DIO voice
  • Java几款性能分析工具的对比 lbwahoo java
    Java几款性能分析工具的对比 摘自：http://my.oschina.net/liux/blog/51800   在给客户的应用程序维护的过程中，我注意到在高负载下的一些性能问题。理论上，增加对应用程序的负载会使性能等比率的下降。然而，我认为性能下降的比率远远高于负载的增加。我也发现，性能可以通过改变应用程序的逻辑来提升，甚至达到极限。为了更详细的了解这一点，我们需要做一些性能
  • JVM参数配置大全 nickys jvm应用服务器
    JVM参数配置大全 /usr/local/jdk/bin/java -Dresin.home=/usr/local/resin -server -Xms1800M -Xmx1800M -Xmn300M -Xss512K -XX:PermSize=300M -XX:MaxPermSize=300M -XX:SurvivorRatio=8 -XX:MaxTenuringThreshold=5 -
  • 搭建 CentOS 6 服务器(14) - squid、Varnish rensanning varnish
    （一）squid 安装 # yum install httpd-tools -y # htpasswd -c -b /etc/squid/passwords squiduser 123456 # yum install squid -y 设置 # cp /etc/squid/squid.conf /etc/squid/squid.conf.bak # vi /etc/
  • Spring缓存注解@Cache使用 tom_seed spring
    参考资料 http://www.ibm.com/developerworks/cn/opensource/os-cn-spring-cache/ http://swiftlet.net/archives/774   缓存注解有以下三个： @Cacheable      @CacheEvict     @CachePut
  • dom4j解析XML时出现"java.lang.noclassdeffounderror: org/jaxen/jaxenexception"错误 xp9802
    java.lang.NoClassDefFoundError: org/jaxen/JaxenExc 关键字: java.lang.noclassdeffounderror: org/jaxen/jaxenexception 使用dom4j解析XML时，要快速获取某个节点的数据，使用XPath是个不错的方法，dom4j的快速手册里也建议使用这种方式 执行时却抛出以下异常： Exceptio
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他