基于BP神经网络的手写体数字识别matlab仿真实现

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

      文字、数字识别是一个典型的模式识别问题，也是模式识别中一个非常重要的应用领域。在文字、数字识别系统中，手写体的文字与识别是一个较难的领域，但却具有极大地应用意义。手写体字符识别作为一种信息处理的手段，具有广阔的应用背景，例如签名的自动识别、邮政编码的自动识别等等，都在信息化时代给人们带来了极大的便利。

      通常，字符的识别在预处理阶段都需要图像处理技术，人在识别字符时也是这样一个过程，即看到字符，将字符一个个分开，然后再对字符进行识别，因此，字符识别系统包括字符图像读取、字符分割及识别三个部分。

       手写体字符的识别是多年来的研究热点，在过去的数十年中，研究者们提出了许许多多的识别方法。数字识别问题是根据待识别数字符号的特征观察值将其分类到0-9共10个类别中去。手写体数字识别方法大致可以分为两类[3]:基于统计的识别方法和基于结构的识别方法。

      统计法所使用的技术大致有一下几类:

1) 模板匹配法

2) 从像素点统计分布的角度来抽取特征，主要的方法有:采样点方法，矩方法、特征轨迹方法等。

3) 用全局变换和级数展开的方法抽取特征。全局变换和级数展开可以减少特征向量的维数，且对于一些全局的形变，如平移和旋转，具有一定的不变性。

上述统计方法中，对仅使用单个特征的分类器而言，其识别率还不够高。

       对结构方法而言，它一般是通过分析字符的轮廓或骨架来取得字符的几何和拓扑特征，如环路、端点、弧状线及凹凸性等等。

       一般来说，结构方法有较高的识别速度，而且对于字符的变形具有良好的抗干扰能力，同时对字符的旋转，平移和伸缩具有较好的稳定性，但是这种方法的特征抽取过程比较复杂，由于特征定义和抽取都直接依赖于研究者的直觉，对图像预处理要求较高。

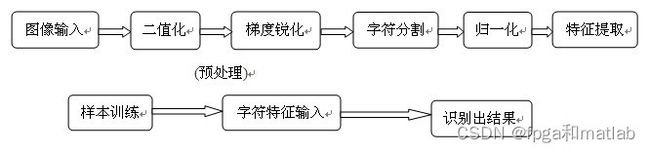
       识别字体的过程首先是要在输入图像后进行预处理[8~9]，预处理一般包括二值化、行字切分、平滑、去噪声、规范化和细化等。不同的识别方法对预处理的要求不同。

       所谓的二值化(Binarization)就是指把字符灰度图像处理成二值(0, 1)图像的过程。对灰度图像二值化能显著地减小数据存储的容量，降低后续处理的复杂度。其次，在二值化后利用均值滤波的方法消除孤立点、线的噪声，这样图中就只剩下手写体数字。平滑去噪后，对图像进行规范化处理。找出图像中数字的边界，然后提取出数字把它举重放置在正方形方框中，再对此正方形图像进行线性插值缩放，使它变为统一规格大小的图像。接下来，要对手写体数字进行细化。

数字图像预处理前后效果比较如图1.1与图1.2，图2.1与图2.2所示。

              

         在对字体进行预处理后要进行的是特征的提取，选取图像的灰度特征时要考虑到特征量的维数与识别的准确率的要求。例如，我们将字符归—化为17像素×8像素点阵图．按每个像素位为0或1，形成网络的136个输入特征值，如图3所示。

       得到的特征图像是二值图像，对应一个元素为0和l的17像素×8像素的特征矩阵，然后是对特征图像编码。编码规则是，按照从左至右、从上到下的顺序，依次扫描整个特征矩阵，将每一行的0和1转换成一个136像素×1像素的特征列。将每一个字符都进行编码后，顺序送送入已经训练好的神经网络识别，识别结果最后以文本格式输出。

       BP网络一般为多层神经网络。BP网络的信息从输入层流向输出层，因此是一种多层前馈神经网络。多层BP网络算法实现的简单流程如图5所示。

       然而孙光民等人利用非线性 PCA神经网络对手写体字符进行识别的研究，非线性PCA算法的神经网络结构如图所示。

        手写体数字的识别种类虽然比汉字、字母少很多，但是由于本文提到的那些难点，且其应用领域也必将会拓展到金融、税务等以数字为主的各行业中，数字识别必将要提高到一定准确率，因此，提高单个数字的识别率，降低拒识率和误识率仍然是研究者们需要努力的方向。

二、核心程序

%形成输入矢量P和目标矢量t的matlab程序
clear all;
filename = dir('*.JPG');     %图像文件格式
for k=1:100
    p1=ones(16,16);          %缩放后用于存储的像素空间
    x=imread(filename(k).name);  %读取图像文件
    bw=im2bw(x,0.5);             %二值化
  [i,j]= find(bw==0);            %寻找数字所在的像素索引
   imin=min(i);                  %求取数字像素占据空间的最小行索引
   imax=max(i);                  %求取数字像素占据空间的最大行的索引
   jmin=min(j);                  %求取数字像素占据空间的最小列的索引
   jmax=max(j);                  %求取数字像素占据空间的最大列的索引 
   bwl=bw(imin:imax,jmin:jmax);  %把图像由39×39缩放为实际数字像素所需的空间
   rate=16/max(size(bwl));       %求取放大比率
   bwl=imresize(bwl,rate);       %按比率放大图像
   [i,j]=size(bwl);              %求取行列数
  i1=round((16-i)/2);            %取整
   j1=round((16-j)/2);
   p1(i1+1:i1+i,j1+1:j1+j)=bwl;  %图像从右向暂存
   p1=-1.*p1+ones(16,16);        %将图像反色
   for m=0:15                    %样本特征存于输入矢量
       p(m*16+1:(m+1)*16,k+1)=p1(1:16,m+1);
   end
switch k                         %对应各个输入样本求取对应的目标矢量
    case{ 1,2,3,4,5,6,7,8,9,10}
      t(k+1)=0;
    case{ 11,12,13,14,15,16,17,18,19,20}
      t(k+1)=1;
    case{ 21,22,23,24,25,26,27,28,29,30}
        t(k+1)=2; 
    case{ 31,32,33,34,35,36,37,38,39,40}
         t(k+1)=3;
     case{ 41,42,43,44,45,46,47,48,49,50}
         t(k+1)=4;
    case{ 51,52,53,54,55,56,57,58,59,60}
         t(k+1)=5;
   case{ 61,62,63,64,65,66,67,68,69,70}
        t(k+1)=6;
   case{ 71,72,73,74,75,76,77,78,79,80}
       t(k+1)=7;
    case{ 81,82,83,84,85,86,87,88,89,90}
       t(k+1)=8;
     case{ 91,92,93,94,95,96,97,98,99,100}
        t(k+1)=9;
    end
end
save swjPT p t;                                   %保存输入矢量和目标矢量

%样本训练
clear all;
load swjPT p t;       %加载输入矢量和目标矢量
pr(1:256,1)=0;        %初始权值设计
pr(1:256,2)=1;
net=newff(pr,[25 1],{'logsig','purelin'},'traingdx','learngdm'); %神经网络初始化

net.trainParam.epocha=4500;                 %训练次数
net.trainParam.goal=0.001;                  %训练误差
net.trainParam.show=10;                     %显示间隔
net.trainParam.lr=0.09;                     %学习率
net=train(net,p,t);                         %样本训练
save swjnet net;                            %保存训练好的网络

三、测试结果

变会识别数字4；

 A10-02