基于BP神经网络的数字识别

主要内容

1.课题研究背景

• 2 图像预处理
• 3 模式识别
• 4识别效果
• 5总结

1. 课题研究背景

 近年来,人工神经网络技术取得了巨大的发展,它所具有的优势：固有的并行结构和并行处理、知识的分布存储、容错性、自适应性、模式识别能力,为手写体数字识别开辟了新的途径。

 数字识别作为模式识别的一个重要分支,在邮政、税务、交通、金融等行业的实践活动中有着及其广泛的应用。

 数字识别作为模式识别领域的一个重要问题，也有着重要的理论价值。一方面，阿拉伯数字是世界各国通用 的符号，因此，数字是一个重要枢纽。在符号识别领域， 数字识别为这一领域提供了一个算法研究的平台。另一方 面，数字的识别方法很容易推广到其它一些相关问题，特 别是对英文字母的识别，但到目前为止机器的识别本领还 无法与人的认知能力相比，这仍是一个有难度的开放问题。

1.1.数字识别的发展现状

 模式识别 (Pattern Recognition)是对表征事物或现象的各种形式的(数值的、文字的和逻辑关系的)信息进行处理和分析，以对事物或现象进行描述、辨认、分类和解释的过程。它是信息科学和人工智能的重要组成部分。而数字识别作为模式识别的一个分支。在日常生活和科研中具有十分重要的作用。数字识别的算法一般是采用以知识、神经网络、人工智能为基础的模板匹配法、轮廓多边形相关、傅立叶系数法等方法来进行识别的。以上方法识别效率高，但是实现较为复杂。

图像预处理

• (1)彩色图像的灰度化,图像输入后一般都是256色彩色图像，灰度化后灰度图像的RGB值是相等的，灰度值为255的像素为白色，灰度值为0的像素为黑色。
• (2)灰度图像的二值化,彩色图像灰度化后每像素只有一个值，即灰度值，二值化就是根据一定标准将图像分成黑白二色。
• (3)梯度锐化,梯度锐化同时对噪声也起一定的去除作用，采取Roberts算子对图像锐化，可以让模糊的边缘变清楚，同时选用合适阈值可以减弱和消除细小的噪声。
• (4)去离散噪声,扫描整个图像，当发现一个黑色像素就考察和它直接或间接相连的黑色像素有多少，如果大于一定值（具体数值视情况定），就可以认为它非离散点，否则就认为他是离散点，将其从图像中去掉。
• (5)归一化调整, 先得到原来字符的高度，并与系统要求的高度比较，得出高度变换系数，然后根据这个系数得到变换后应有的宽度，得出高度、宽度后，把新图像里的点按照插值的方法映射到原图像。

图像输入

灰度转化

二值化

图像锐化

归一化

去除噪声

图1 图像处理流程

模式识别

3.1.特征提取

 经过预处理，把原来大小不同、分布不规律的各字符变成大小一样、排列整齐的字符。下面要从预处理完的字符中提取最能体现这一个字符的特征向量，将提取出的训练样本中的特征向量代入BP网络中就可以对BP网络进行训练。提取出待识别的样本中特征向量代入训练好的BP网络中就可以进行识别。在这里采取逐像素特征提取法，方法是对图像进行逐行逐列扫描，当遇到黑色像素时，取其特征值为1，当遇到白色像素时，取其特征值为0。这样扫描结束后就形成一个维数与图像中像素点的个数相同的特征向量矩阵。

3.2. BP神经网络

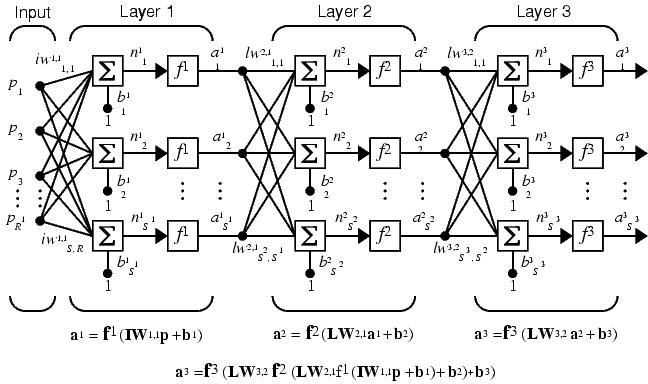
3.2.1. BP算法的多层感知器

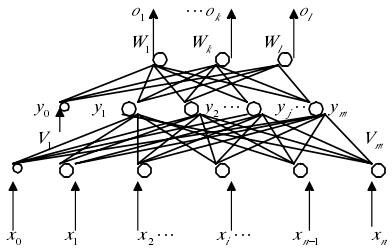
图2 三层BP网

采用BP算法的多层感知器是至今为止应用最广泛的神

经网络，在多层感知器的应用中，一般习惯将单隐层感知器称为三层感知器，所谓三层包括了输入层、隐层和输出层。

1. BP算法的多层感

知器

反向传播(Backpropagation)算法：从后向前

（反向）逐层“传播”输出层的误差，以间接算出隐层误差。分两个阶段：

• • • • • 正向过程：从输入层经隐层逐层正向计算各单元的输出。
        • 反向过程：由输出层误差逐层反向计算隐层各单元的误差，并用此误差修正当前层的权值。

正向过程

• • • • 正向过程:

a ( k ) 

f ( n

BP

算法

( k ) )

j j

n ( k ) 

i

w ( k

) a ( k

 1 )  

w ( k ) a

( k  1 )

j j i j i

梯度下降(gradient decent)

BP

算法

法

• 准则函数: sum squared error, SSE

1 S 2 1 T

j

J  s s e 

2 S 

( t j

• a j )

 ( t 

2 S

a ) ( t  a )

• 权值修正: 梯度下降法

 w  

 J

   J

 n j

   J

a ( k

 1 )

j  w  n  w  n

j j j j

Case 1: 输出层权值修正

BP

算法

   J

局部梯度

  J  a j

  ( t

 a ) f ' ( n )

j

j  n

j

 a j  n j

j j j

扩展delta 学习规则

 w j   j

a ( k  1 )

 ( t j

• a j ) f

' ( n

) a ( k  1 )

1 ' e  n

a  f

( n ) 

1  e  n

f ( n ) 

(1 

e  n ) 2

 a (1  a )

 w j

 ( t j

• a j ) a

j (1 

a j ) a

( k  1 )

Case 2:隐层权值修正 算法

BP

后层的全部单元

 J

i

 j 

   J

 n ( k  1 )

 a j

都受nj的影响

 n j i  n i

   w f ' ( n )

 a j

 n j

nj w ni i

i j i j

i

aj ji

 w  

a ( k

 1 )

 ( 

 w f

' ( n

) )a

( k  1 )

j j i j i j

i

δj δi

w

ji

局部梯度的反向传播

1. BP算法过程

BP

算法

初始值选择

W ( 0 )

1. 前向计算，求出所有神经元的输出

a k ( t )

对输出层计算δ

 j 

( t j

• a j ) a

j (1 

a j )

反向计算：从后向前计算各隐层δ

 j 

a j (1 

a j ) 

i

w j ii

计算并保存各权值修正量：

 w i j

  j a i

修正权值：

w i j ( t

 1 ) 

w i j ( t )

•  w i j

判断是否收敛，如果收敛则结束，不收敛则转至Step 2

3.2.2.BP算法过程

图3 BP学习算法的流程图

3.3BP神经网络设计与训练

 (1)BP神经网络的设计方法

 按照BP神经网络设计方法选用两层BP网络。采用newff函数来建立BP网络。其输入节点数为16×16＝256，隐层传输函数为Sigmoid函数。假设用一个输出节点表示10个数字，则输出层传输函数为pureline，隐层节点数为 ，取25。

 (2)神经网络仿真程序设计

 构造训练样本集，并构成训练所需的输入向量p和目标向量t. 通过画图工具获得数字。本例构造了新宋体12号、8号字体各10 个，黑体12号、8号各10个，及宋体加粗18号字体。

 (3)神经网络测试。

 由于图像处理的复杂性，对于不同噪声的污染选择不同的方法，选择没有噪声的数字进行测试。选择训练样本中的任意数据进行测试，结构非常正确。选择生成的新宋体8号大小的数字进行测试。结果正确，选择其他类型的字体进行测试，则结果不是完全正确。

仿真实验识别效果

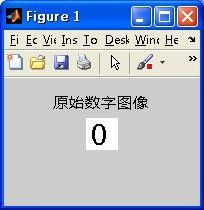
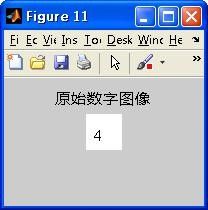
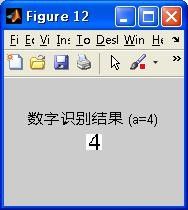
图4 数字0的识别效果 图5 数字4的识别效果

总结

 本课题结合神经网络技术，对数字识别问题进行了探讨和研究，主要研究成果如下：(1)针对数字数据，首先进行了灰度化、二值化、平滑去噪、归一化、细化等常规预处理，然后对处理完的数字图像进行特征提取， 提取了能体现字符特点的特征向量。(2)针对数字识别问题，研究了BP神经网络分类器的建立和识别过程。

 仿真结果表明，对于字体和字号与训练样本集相同 的测试样本，无论图像中的数字在什么位置，都可以识 别出来，而对于字体和字号与训练样本集不同的测试样 本，只有一部分能正确识别。并且对于带有噪声的数字， 运行程序的实验结果是不理想的，所以本课题程序有待 于进一步的整理和调试。为提高识别率，可以增加训练 样本，或通过增加字体的特征向量等途径来解决。

基于BP神经网络的数字识别

主要内容

1.课题研究背景

• 2 图像预处理
• 3 模式识别
• 4识别效果
• 5总结

1. 课题研究背景

 近年来,人工神经网络技术取得了巨大的发展,它所具有的优势：固有的并行结构和并行处理、知识的分布存储、容错性、自适应性、模式识别能力,为手写体数字识别开辟了新的途径。

 数字识别作为模式识别的一个重要分支,在邮政、税务、交通、金融等行业的实践活动中有着及其广泛的应用。

 数字识别作为模式识别领域的一个重要问题，也有着重要的理论价值。一方面，阿拉伯数字是世界各国通用 的符号，因此，数字是一个重要枢纽。在符号识别领域， 数字识别为这一领域提供了一个算法研究的平台。另一方 面，数字的识别方法很容易推广到其它一些相关问题，特 别是对英文字母的识别，但到目前为止机器的识别本领还 无法与人的认知能力相比，这仍是一个有难度的开放问题。

1.1.数字识别的发展现状

 模式识别 (Pattern Recognition)是对表征事物或现象的各种形式的(数值的、文字的和逻辑关系的)信息进行处理和分析，以对事物或现象进行描述、辨认、分类和解释的过程。它是信息科学和人工智能的重要组成部分。而数字识别作为模式识别的一个分支。在日常生活和科研中具有十分重要的作用。数字识别的算法一般是采用以知识、神经网络、人工智能为基础的模板匹配法、轮廓多边形相关、傅立叶系数法等方法来进行识别的。以上方法识别效率高，但是实现较为复杂。

图像预处理

• (1)彩色图像的灰度化,图像输入后一般都是256色彩色图像，灰度化后灰度图像的RGB值是相等的，灰度值为255的像素为白色，灰度值为0的像素为黑色。
• (2)灰度图像的二值化,彩色图像灰度化后每像素只有一个值，即灰度值，二值化就是根据一定标准将图像分成黑白二色。
• (3)梯度锐化,梯度锐化同时对噪声也起一定的去除作用，采取Roberts算子对图像锐化，可以让模糊的边缘变清楚，同时选用合适阈值可以减弱和消除细小的噪声。
• (4)去离散噪声,扫描整个图像，当发现一个黑色像素就考察和它直接或间接相连的黑色像素有多少，如果大于一定值（具体数值视情况定），就可以认为它非离散点，否则就认为他是离散点，将其从图像中去掉。
• (5)归一化调整, 先得到原来字符的高度，并与系统要求的高度比较，得出高度变换系数，然后根据这个系数得到变换后应有的宽度，得出高度、宽度后，把新图像里的点按照插值的方法映射到原图像。

图像输入

灰度转化

二值化

图像锐化

归一化

去除噪声

图1 图像处理流程

模式识别

3.1.特征提取

 经过预处理，把原来大小不同、分布不规律的各字符变成大小一样、排列整齐的字符。下面要从预处理完的字符中提取最能体现这一个字符的特征向量，将提取出的训练样本中的特征向量代入BP网络中就可以对BP网络进行训练。提取出待识别的样本中特征向量代入训练好的BP网络中就可以进行识别。在这里采取逐像素特征提取法，方法是对图像进行逐行逐列扫描，当遇到黑色像素时，取其特征值为1，当遇到白色像素时，取其特征值为0。这样扫描结束后就形成一个维数与图像中像素点的个数相同的特征向量矩阵。

3.2. BP神经网络

3.2.1. BP算法的多层感知器

图2 三层BP网

采用BP算法的多层感知器是至今为止应用最广泛的神

经网络，在多层感知器的应用中，一般习惯将单隐层感知器称为三层感知器，所谓三层包括了输入层、隐层和输出层。

1. BP算法的多层感

知器

反向传播(Backpropagation)算法：从后向前

（反向）逐层“传播”输出层的误差，以间接算出隐层误差。分两个阶段：

• • • • • 正向过程：从输入层经隐层逐层正向计算各单元的输出。
        • 反向过程：由输出层误差逐层反向计算隐层各单元的误差，并用此误差修正当前层的权值。

正向过程

• • • • 正向过程:

a ( k ) 

f ( n

BP

算法

( k ) )

j j

n ( k ) 

i

w ( k

) a ( k

 1 )  

w ( k ) a

( k  1 )

j j i j i

梯度下降(gradient decent)

BP

算法

法

• 准则函数: sum squared error, SSE

1 S 2 1 T

j

J  s s e 

2 S 

( t j

• a j )

 ( t 

2 S

a ) ( t  a )

• 权值修正: 梯度下降法

 w  

 J

   J

 n j

   J

a ( k

 1 )

j  w  n  w  n

j j j j

Case 1: 输出层权值修正

BP

算法

   J

局部梯度

  J  a j

  ( t

 a ) f ' ( n )

j

j  n

j

 a j  n j

j j j

扩展delta 学习规则

 w j   j

a ( k  1 )

 ( t j

• a j ) f

' ( n

) a ( k  1 )

1 ' e  n

a  f

( n ) 

1  e  n

f ( n ) 

(1 

e  n ) 2

 a (1  a )

 w j

 ( t j

• a j ) a

j (1 

a j ) a

( k  1 )

Case 2:隐层权值修正 算法

BP

后层的全部单元

 J

i

 j 

   J

 n ( k  1 )

 a j

都受nj的影响

 n j i  n i

   w f ' ( n )

 a j

 n j

nj w ni i

i j i j

i

aj ji

 w  

a ( k

 1 )

 ( 

 w f

' ( n

) )a

( k  1 )

j j i j i j

i

δj δi

w

ji

局部梯度的反向传播

1. BP算法过程

BP

算法

初始值选择

W ( 0 )

1. 前向计算，求出所有神经元的输出

a k ( t )

对输出层计算δ

 j 

( t j

• a j ) a

j (1 

a j )

反向计算：从后向前计算各隐层δ

 j 

a j (1 

a j ) 

i

w j ii

计算并保存各权值修正量：

 w i j

  j a i

修正权值：

w i j ( t

 1 ) 

w i j ( t )

•  w i j

判断是否收敛，如果收敛则结束，不收敛则转至Step 2

3.2.2.BP算法过程

图3 BP学习算法的流程图

3.3BP神经网络设计与训练

 (1)BP神经网络的设计方法

 按照BP神经网络设计方法选用两层BP网络。采用newff函数来建立BP网络。其输入节点数为16×16＝256，隐层传输函数为Sigmoid函数。假设用一个输出节点表示10个数字，则输出层传输函数为pureline，隐层节点数为 ，取25。

 (2)神经网络仿真程序设计

 构造训练样本集，并构成训练所需的输入向量p和目标向量t. 通过画图工具获得数字。本例构造了新宋体12号、8号字体各10 个，黑体12号、8号各10个，及宋体加粗18号字体。

 (3)神经网络测试。

 由于图像处理的复杂性，对于不同噪声的污染选择不同的方法，选择没有噪声的数字进行测试。选择训练样本中的任意数据进行测试，结构非常正确。选择生成的新宋体8号大小的数字进行测试。结果正确，选择其他类型的字体进行测试，则结果不是完全正确。

仿真实验识别效果

图4 数字0的识别效果 图5 数字4的识别效果

总结

 本课题结合神经网络技术，对数字识别问题进行了探讨和研究，主要研究成果如下：(1)针对数字数据，首先进行了灰度化、二值化、平滑去噪、归一化、细化等常规预处理，然后对处理完的数字图像进行特征提取， 提取了能体现字符特点的特征向量。(2)针对数字识别问题，研究了BP神经网络分类器的建立和识别过程。

 仿真结果表明，对于字体和字号与训练样本集相同 的测试样本，无论图像中的数字在什么位置，都可以识 别出来，而对于字体和字号与训练样本集不同的测试样 本，只有一部分能正确识别。并且对于带有噪声的数字， 运行程序的实验结果是不理想的，所以本课题程序有待 于进一步的整理和调试。为提高识别率，可以增加训练 样本，或通过增加字体的特征向量等途径来解决。