卡尔曼滤波器（Kalman Filter，KF）算法及仿真

在python下完成卡尔曼滤波的模拟采样与迭代

---

卡尔曼滤波器（Kalman Filter，KF）算法及仿真

参考链接 我的大学老师刘二大人
刘二大人永远的神
github工程如下 ： 点我

---

提示：以下是本篇文章正文内容，下面案例可供参考

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

1. 贝叶斯滤波器

贝叶斯滤波器的算法如下所示：

---

1：Algorithm Bayes_filter$(bel(x_{t-1}),u_t,z_t)$:
2：  for all $x_t$ do
3：    $\overline{bel}(x_t)=\int p(x_t|u_t,x_{t-1})bel(x_{t-1})d{x}_{t-1}$
4：    $bel(x_t)=\eta p(z_t|x_t)\overline{bel}(x_t)$
5：  end for
6：  return $bel(x_t)$

---

贝叶斯滤波的生成模型也被称为隐马尔科夫模型（Hidden Markov Model，HMM）或动态贝叶斯网络（Dynamic Bayes Network， DBN）。

对于离散有限的状态空间，可以用所有可能状态的概率值来表示置信度。但是如果状态空间是无限或连续，则置信度难以表示。

通常有两种置信度的表示方法：

1. 用多元正态分布来表示置信度。对应的滤波算法被称统称为高斯滤波（Gaussian Filter）。
2. 用粒子集来表示置信度。对应的滤波算法被称为粒子滤波（Particle Filter）。

---

2. 卡尔曼滤波

KF算法用矩来定义置信度，可以对连续状态的置信度进行计算，但是不适用于离散状态空间和混合状态空间。

---

1：Algorithm Kalman_filter$({\mu }_{t-1},{\Sigma }_{t-1},u_t,z_t)$:
2：  ${\overline{\mu }}_t=A_t{\mu }_{t-1}+B_t{u}_t$
3：  ${\overline{\Sigma }}_t=A_t{\Sigma }_{t-1}{A}_t^T+R_t$
4：  $K_t={\overline{\Sigma }}_t{C}_t^T(C_t{\overline{\Sigma }}_t{C}_t^T+Q_t{)}^{-1}$
5：  ${\mu }_t={\overline{\mu }}_t+K_t(z_t-C_t{\overline{\mu }}_t)$
6：  ${\Sigma }_t=(I-K_t{C}_t){\overline{\Sigma }}_t$
7：  return ${\mu }_t,{\Sigma }_t$

---

# 3. Kalman Filter仿真

3.1 仿真模型

3.1.1 问题描述

假设有一个沿直线运动的机器人，每隔一个时间间隔$△t$，根据运动$u_t$对自己当前的状态进行预测（Predict），然后利用传感器获得的测量$z_t$对自己的状态进行更新（Update）。

定义机器人的状态$x_t=\left[\begin{array}{c}{p}_t\\ v_t\end{array}\right]$，其中$p_t$表示机器人的位置，$v_t$表示机器人的速度。

3.1.2 运动模型

假设机器人可以控制其加速度$a$，则运动迁移方程可以写为：
KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ p_t &= p_{t-1}…

把该方程改写为线性方程，可得：
KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ x_t &= \begin{…

其中${\epsilon }_t$是控制带来的噪声，假设加速度$a$包含有一个$\sim N(\mu ,{\sigma }_a^2)$的一个噪声。因此该噪声对机器人状态$x_t$带来的噪声可表示为：$ noise_u \sim N(\mu , R_t)$，其中$\mu = (0, 0)^T$，$R_t = \begin{bmatrix} ({\frac 12 \triangle t^2})2 & 0 \ 0 & ({\triangle t})^2 \end{bmatrix} \sigma_u^2$。

3.1.3 测量模型

贝叶斯滤波的测量模型并不是使用后验概率$p(x|z)$，而是用似然（likelihood）来进行计算。

假设该仿真模型中的机器人可以获得对当前位置的一个测量量$z_t$，因此可以得到测量模型为：
KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ z_t &= p_t + \…

其中${\delta }_t$是测量的噪声，该噪声遵从一个均值为0的高斯分布${\delta }_t\sim N(\mu ,{\sigma }_z^2)$。

---

3.2 仿真实验设计

3.2.1 采样函数

在真实的机器人系统中，当我们给定一个控制$u_t$，控制系统将会带有噪声的执行这个控制，在真实物理环境下我们的目的就是去恢复带噪声的执行结果。

在仿真的过程中，我们通过一些采样函数根据控制$u_t$来随机的采样，并将采样的结果作为真实的运动结果，然后就可以观察是否可以通过卡尔曼滤波来消除控制$u_t$所产生的累计噪声。

通常在采样的时候，我们使用正态分布（Normal Distribution）或者三角分布（Triangle Distribution）。

a) 正态分布/高斯分布

正态分布的密度函数为：
$$p(x)=\frac{1}{\sqrt{2\pi {\sigma }_2}}{e}^{-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}}$$

由于在概率机器人模型中，通常假设分布的均值为$0$，因此均值为$0$的正态分布的密度函数为：
$$p(x)=\frac{1}{\sqrt{2\pi {\sigma }_2}}{e}^{-\frac{1}{2}\frac{x^2}{{\sigma }^2}}$$

---

3.2.2 运动采样

回忆之前的运动控制方程：

由图片所示

为了仿真出机器人真实的路径，采用采样的方式来计算真实的机器人状态。在后面根据这个状态来获得观测。

# 控制采样函数，为简化模型我们选用delta t为1
sigma_u = 0.2
def sample_pose(x0, u, sigma):
    A = np.array([1, 1, 0, 1]).reshape((2, 2))
    B = np.array([0.5, 1]).reshape((2, 1))
    noise = np.random.normal(0, sigma)
    x0 = np.array(x0).reshape((2, 1))
    x1 = np.dot(A, x0) + B * u + B * noise
    return x1

sample_pose([0, 0], 1, sigma_u)

---

3.2.3 测量采样

在这个仿真实验中，机器人只有一个传感器，可以直接获得对机器人位置的测量，因此有下面的测量模型：

# 测量采样函数
sigma_z = 0.1
def sample_measurement(x, sigma):
    C = np.array([1, 0]).reshape((1, 2))
    x = np.array(x).reshape((2, 1))
    noise = np.random.normal(0, sigma, size=(1, 1))
    z = np.dot(C, x) + noise
    return z

sample_measurement([1, 2], sigma_z)

---

3.2.4 生成控制序列

在仿真中假设我们共进行10次Kalman Filter迭代，每一次运动的控制$u_t$（也就是加速度$a_t$）的值，通过均匀采样得到。

N = 10
U = np.random.uniform(0, 1, size=N)
U

---

3.2.5 根据控制序列生成无滤波的状态估计

无滤波的状态估计本质上是在假设控制是没有误差的，因此会和真实情况产生巨大的偏移。

假设初始状态$x_0=(0,0{)}^T$。

# 根据上一时刻的状态和当前控制，来估计当前时刻的状态
def caculate_pose(x0, u):
    A = np.array([1, 1, 0, 1]).reshape((2, 2))
    B = np.array([0.5, 1]).reshape((2, 1))
    x0 = np.array(x0).reshape((2, 1))
    x1 = np.dot(A, x0) + B * u
    return x1

x0 = np.array([0, 0]).reshape((1, 2))
X_no_filter = x0

for u in U:
    x = caculate_pose(X_no_filter[-1], u)
    X_no_filter = np.vstack([X_no_filter, np.array(x).reshape((1, 2))])

fig, ax = plt.subplots()
plt.plot(X_no_filter[:, 0], X_no_filter[:,1], label='no-filter')
ax.set_xlabel('Position')
ax.set_ylabel('Velocity')
ax.legend(loc='lower right')

---

3.2.6 通过采样获得Ground Truth状态

通过对状态进行采样，来仿真真实情况下，带有噪声的控制所产生的运动结果。

x0 = np.array([0, 0]).reshape((1, 2))
X_ground_truth = x0

for u in U:
    x = sample_pose(X_ground_truth[-1], u, sigma=0.2)
    X_ground_truth = np.vstack([X_ground_truth, np.array(x).reshape((1, 2))])


fig, ax = plt.subplots()  
ax.plot(X_no_filter[:, 0], X_no_filter[:,1], c='b', marker='o', label='no-filter')
ax.plot(X_ground_truth[:,0], X_ground_truth[:,1], c='k', marker='o', label='ground-truth')
ax.set_xlabel('Position')
ax.set_ylabel('Velocity')
ax.legend(loc='lower right')

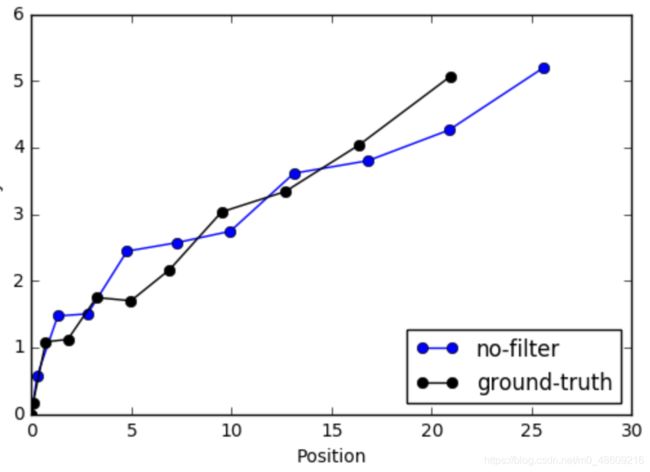
从上图可以看出，当控制$u_t$带有噪声的运行时，无滤波的位姿推断与Ground-Truth之间存在着较大的差异，而且随着时间的变化，其差异会越来越大。

可以通过修改的N，来改变状态的数量，以观察这种随机漂移的现象。

---

3.2.7 根据Ground-Truth状态来生成测量的采样数据

由于传感器观测的是外部物理世界，因此在仿真中，我们根据Ground-Truth的状态来生成带有误差的测量。

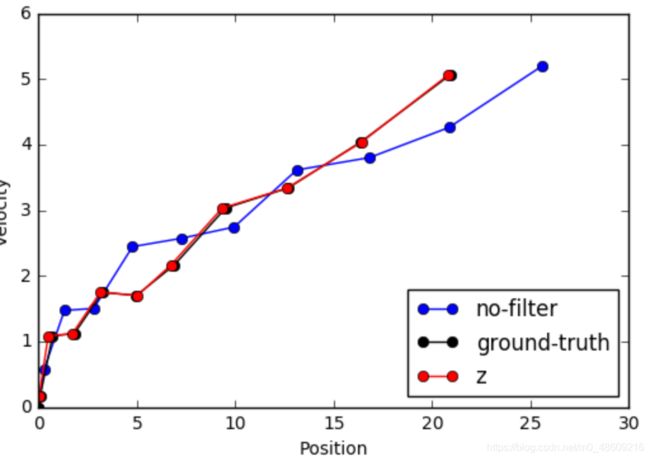
但是观测$z_t$并不包含速度的信息，因此在下面的图中，使用Ground-Truth的速度信息来作为观测曲线。因此注意观察红色曲线在水平方向上与Ground-Truth的偏移。

Z = []
for x in X_ground_truth[1:]:
    Z.append(sample_measurement(x, sigma=0.1))

fig, ax = plt.subplots()
ax.plot(X_no_filter[:, 0], X_no_filter[:,1], c='b', marker='o', label='no-filter')
ax.plot(X_ground_truth[:,0], X_ground_truth[:,1], c='k', marker='o', label='ground-truth')
ax.plot(np.squeeze(Z), X_ground_truth[1:,1], c='r', marker='o', label='z')
ax.set_xlabel('Position')
ax.set_ylabel('Velocity')
ax.legend(loc='lower right')

---

3.2.8 利用Kalman Filter进行滤波

回忆之前给出的Kalman Filter算法：

---

1：Algorithm Kalman_filter$(\mu ,{\Sigma }_{t-1},u_t,z_t)$:
2：  ${\overline{\mu }}_t=A_t{\mu }_{t-1}+B_t{u}_t$
3：  ${\overline{\Sigma }}_t=A_t{\Sigma }_{t-1}{A}_t^T+R_t$
4：  $K_t={\overline{\Sigma }}_t{C}_t^T(C_t{\overline{\Sigma }}_t{C}_t^T+Q_t{)}^{-1}$
5：  ${\mu }_t={\overline{\mu }}_t+K_t(z_t-C_t{\overline{\mu }}_t)$
6：  ${\Sigma }_t=(I-K_t{C}_t){\overline{\Sigma }}_t$
7：  return ${\mu }_t,{\Sigma }_t$

---

def kalman_filter(mu0, Sigma0, u, z, sigma_u=0.2, sigma_z=0.1):
    # 控制预测方程和测量更新方程所需要的系数矩阵
    A = np.array([1, 1, 0, 1]).reshape((2, 2))
    B = np.array([0.5, 1]).reshape((2, 1))
    C = np.array([1, 0]).reshape((1, 2))
    
    # 控制方程和测量方程的误差协方差矩阵
    R = np.array([0.25, 0, 0 , 1]).reshape((2, 2)) * sigma_u ** 2
    Q = np.array([1]).reshape((1,1)) * sigma_z ** 2    
    #Q是干嘛的 - -
    #R是 协方差矩阵 测量方程的
    
    # 对输入的参数进行Tensor维度上的调整，已进行后面的矩阵计算
    mu0 = np.array(mu0).reshape((2, 1))
    Sigma0 = np.array(Sigma0).reshape((2,2))
    z = np.array(z).reshape((1,1))
    
    # 执行控制预测步骤，实现了上面算法的2-3行
    mu1 = np.dot(A, mu0) + B * u
    Sigma1 = np.dot(np.dot(A, Sigma0), A.T) + R
    
    # 进行测量更新步骤，实现了上面算法的4-6行
    Temp = np.linalg.inv(np.dot(np.dot(C, Sigma1), C.T) + Q)
    K = np.dot(np.dot(Sigma1, C.T), Temp)
    mu2 = mu1 + np.dot(K, (z - np.dot(C, mu1)))
    Sigma2 = np.dot((np.eye(2) - np.dot(K, C)), Sigma1)
    
    # 返回Kalman Filter计算出来的新的时刻的均值和方差
    return mu2, Sigma2

对于矩阵 R 与 Q
R： 两噪声认为独立，所以是只有对角线上元素非0

R 与 Q 分为控制步与预测步

x0 = np.array([0, 0]).reshape((1, 2))
X_kalman_filter = x0

sigma0 = np.array([1, 0, 0, 1]).reshape((2,2))
Sigma_kalman_filter = []
Sigma_kalman_filter.append(sigma0)

for u, z in zip(U, Z):
    x, sigma = kalman_filter(X_kalman_filter[-1], Sigma_kalman_filter[-1],
                             u, z, sigma_u=0.4, sigma_z=0.1)
    X_kalman_filter = np.vstack([X_kalman_filter, x.T])
    Sigma_kalman_filter.append(sigma)

fig, ax = plt.subplots()
ax.plot(X_no_filter[:,0], X_no_filter[:,1], c='b', marker='o', label='no-filter')
ax.plot(X_ground_truth[:,0], X_ground_truth[:,1], c='k', marker='o', label='ground-truth')
ax.plot(X_kalman_filter[:,0], X_kalman_filter[:,1], c='r', marker='o', label='kalman-filter')
ax.set_xlabel('Position')
ax.set_ylabel('Velocity')
ax.legend(loc='lower right')

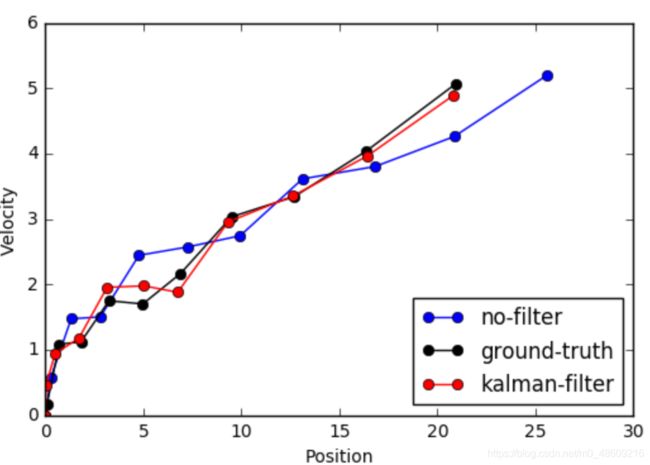
根据上面结果，可以观察到采用kalman滤波后，能够有效的降低误差。

from matplotlib.patches import Ellipse
# 定义函数getEllipse，根据均值和协方差来返回一个Ellipse对象
def getEllipse(mu, sigma):
    mu = np.squeeze(mu)
    
    scale = np.sqrt(5.991) * 2
    e, v = np.linalg.eig(sigma)
    
    if (e[0] < 0 or e[1] < 0):
        raise ValueError
    
    width = np.sqrt(e[0]) * scale
    length = np.sqrt(e[1]) * scale
    alpha = np.degrees(np.arctan(v[1][0]/v[0][0]))
    ell = Ellipse(xy=mu, width=width, height=length, angle=alpha, 
              alpha=0.2, facecolor='none', edgecolor='r', linestyle = '-',  linewidth=1)
    return ell

ells = [getEllipse(mu, sigma) for mu, sigma in zip(X_kalman_filter, Sigma_kalman_filter)]

fig, ax = plt.subplots()

ax.plot(X_no_filter[:,0], X_no_filter[:,1], 
        c='b', marker='o', label='no-filter')

ax.plot(X_ground_truth[:,0], X_ground_truth[:,1],
        c='k', marker='o', label='ground-truth')

ax.plot(X_kalman_filter[:,0], X_kalman_filter[:,1],
        c='r', marker='o', label='kalman-filter')
ax.set_xlabel('Position')
ax.set_ylabel('Velocity')
ax.legend(loc='lower right')

for ell in ells:
    ax.add_artist(ell)
    
# ax.set_xlim([-10, 25])
# ax.set_ylim([-5, 10])

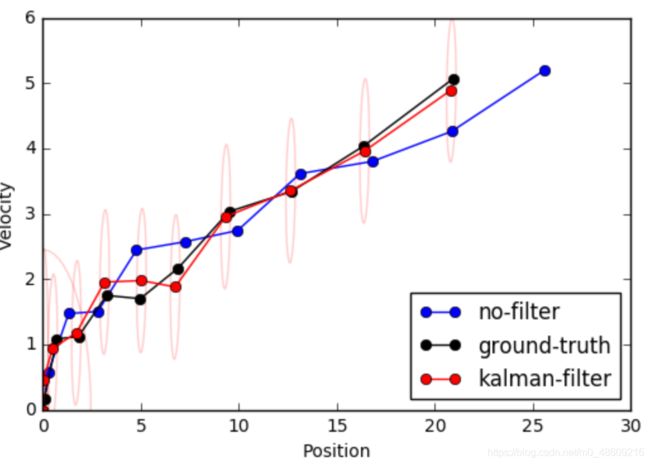
从上图的协方差椭圆可以看到，由于观测无关Velocity，因此垂直方向的不确定较大，而Position方向的不确定性较小。随着滤波过程的进行，不确定性逐渐的收敛。

---

---