cs231n——浅析三种生成模型

一、有监督学习和无监督学习

有监督学习

有监督学习在前面的学习中已经接触了一些，在这种模式下，我们拥有数据data和数据对应的标签label，有监督学习的目的是找到数据x与标签y之间的映射关系，标签的形式也是多样的。常见的有监督学习有以下几种

• 分类：输入图片，输出类别
• 目标检测：输入图片，输出目标物体的边框
• 语义分割：为图像的每一个像素加label
  …
  

无监督学习

在无监督学习中，只有训练数据，没有标签，要学习的是数据的隐藏结构。
比较典型的无监督学习有：

• 聚类：将数据在某种度量方式下分组

• 降维：找出一些轴，在这些轴上训练数据的方差最大。这些轴就是数据内潜在的结构。可以用这些轴来减少数据维度，数据在每个保留下来的维度上都有很大的方差。
  

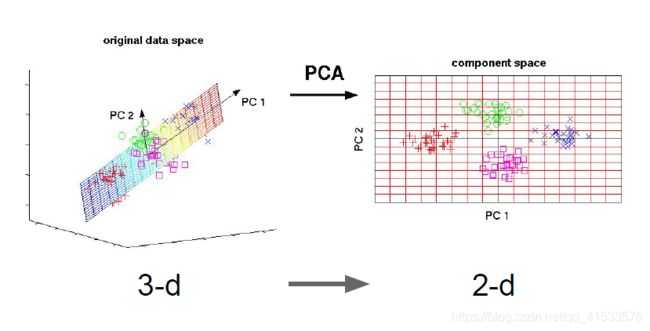
• 密度估计：估计数据的内在分布情况，在上方有一些一维的点，可以尝用一个高斯函数来拟合这一密度分布情况；在下面的例子中，这里是二维数据，我们仍然想拟合出一个模型，这个模型的密度在点集中的地方密度值更高。
  
  …

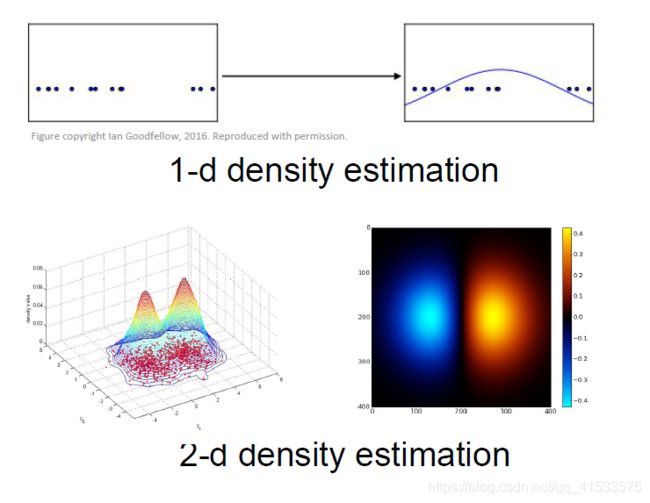
二者对比

二、生成模型

什么是生成模型？

生成模型（Generative Models）：通过已给定的训练数据，从相同的数据分布中生成新的样本

如上图，训练数据服从分布$p_{data}$，生成模型尝试学习到一个模型$p_{model}$来生成模型，$p_{model}$的分布应与$p_{data}$尽量相似。
有两种方式解决这个问题：

1. 显式密度估计：显式定义并求解$p_{model}$

2. 隐式密度估计：学习可以从$p_{model}$采样的模型，而不需要显式定义它

为什么需要生成模型？

可以从数据分布中创造出我们想要的真实样本。左边为生成的图片，中间生成的人脸，还可以做超分辨率或者着色之类的任务。

生成模型的分类

生成模型可以分为两大类任务——显式密度估计模型和隐式密度模型，这两大类又可以继续细分，这里探讨的主要是三种模型，PixelRNN/CNN、变分自动编码器（Variational Autoencoder）与生成对抗网络（GAN），其中前两者属于显式密度估计模型，最后的GAN属于隐式模型。

三、PixelRNN/CNN

PixelRNN和PixelCNN都属于全可见信念网络，要做的是对一个密度分布显示建模。我们有图像数据x，想对该图像的概率分布或者似然p(x)建模，使用链式法则将这一似然分解为一维分布的乘积.

每个像素$x_i$的条件概率，它的条件是给定所有下标小于i的像素（$x_1$到$x_{i-1}$），这时图像中所有像素的概率或联合概率就是所有这些像素点似然的乘积。一旦定义好这些似然，为了训练好这一模型，我们只需要在该定义下最大化训练数据的似然函数。

PixelRNN

从左上角一个一个生成像素，生成顺序为箭头所指顺序，每一个对之前像素的依赖关系都通过RNN来建模。

缺点：顺序生成，速度很慢

PixelCNN

从图像拐角处生成整个图像，区别在于现在使用CNN来对所有依赖关系建模。

对环境区域（图示那个指定像素点的附近区域）上使用CNN，取待生成像素点周围的像素，把它们传递给CNN用来生成下一个像素值，每一个像素位置都有一个神经网络输出，该输出将会是像素的softmax损失值，通过最大化训练样本图像的似然来训练模型，在训练的时候取一张训练图像来执行生成过程，每个像素位置都有正确的标注值（并非人工标注）即训练图片在该位置的像素值，该值也是我们希望模型输出的值。

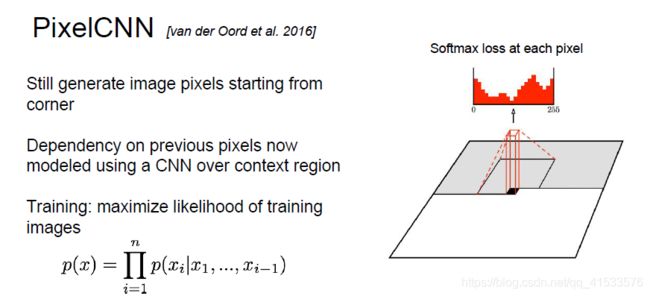
训练比PixelRNN更快，可以并行卷积，因为上下文区域值从训练图像中已知，但是生成仍必须按顺序进行，所以仍然很慢。

总结

PixelRNN和PixelCNN能显式地计算似然p(x)，是一种可优化的显式密度模型，并且给出了一个很好的评估度量，可以通过计算的数据的似然来评价生成样本。
缺点：生成过程序列化，速度慢

四、变分自编码器

对上述的PixelRNN/CNN，所定义的密度函数比较容易处理，即
$$p_{\theta }(x)=\prod _{i=1}^n{p}_{\theta }(x_i|x_1...x_{i-1})$$
可以直接优化函数的似然

在变分自编码模型中，所定义的函数不易处理
$$p_{\theta }(x)=\int p_{\theta }(z)p_{\theta }(x|z)dz$$
通过附加的隐变量z对密度函数进行建模，对所有可能的z值取期望，无法直接优化，只能找出一个似然函数的下界然后再对该下界进行优化。

自编码器

自动编码器并不生成数据，它是一种利用无标签数据来学习低维特征的无监督学习。

输入数据x和特征z，接下来有一个编码器进行映射，来实现从输入数据x到特征z的映射。编码器可以有多种形式，常用的是神经网络。最先提出的是非线性层的线性组合，又有了深层的全连接网络，又出现了CNN。

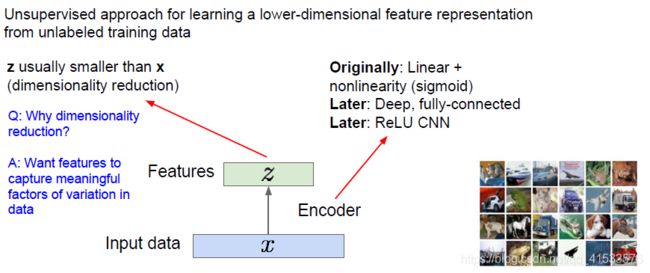
取得输入数据x然后将其映射到某些特征z，再将z映射到比x更小的维度上，由此可以实现降维。 对z进行降维是为了表示x中最重要的特征。

自动编码器将该模型训练成一个能够用来重构原始数据的模型，用编码器将输入数据映射到低维的特征z（也就是编码器网络的输出），同时需要获得基于这些数据得到的特征，然后用第二个网络，也就是解码器输出一些跟x有相同维度并和x相似的$\hat{x}$，也就是重构原始数据。

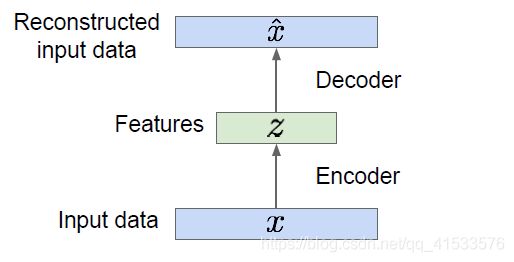
对于解码器，一般使用和编码器相同类型的网络（通常与编码器对称，如upconv和conv）

所以自编码器的流程应为：

Created with Raphaël 2.3.0 开始 取得数据 获取数据特征 特征传给解码器 解码器末端重构数据 结束

为了能够重构输入数据，使用L2损失函数$||x-\hat{x}|{|}^2$，让输入数据中的像素与重构数据中的像素相同。

网络训练结束后，去除解码器，使用训练好的编码器实现特征映射，通过编码器得到输入数据的特征，编码器顶部有一个分类器，如果是分类问题可以用它来输出一个类标签，在这里使用了外部标签和标准的损失函数如softmax。

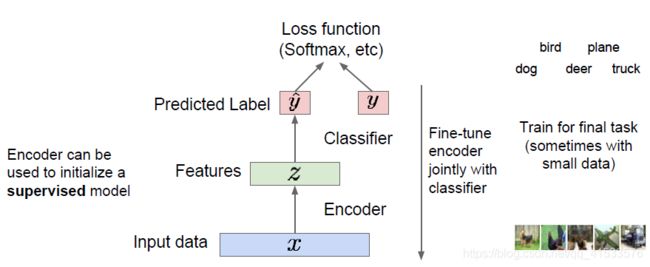
自动编码器重构数据，学习数据特征，初始化一个监督模型的能力。这些学习到的特征具有能捕捉训练数据中蕴含的变化因素的能力。从而可以获得了一个含有训练数据中变化因子的隐变量z。

变分自编码器

此部分还未明白，今后补充。

五、生成对抗网络（GANs）

前面提到，GAN是一种隐式密度估计模型，放弃显式地对密度函数建模，而是从分布中采样并获得质量良好的样本。

这个过程如同两个玩家的博弈，一个玩家是生成器网络，一个是判别器网络。生成器网络作为玩家1会试图骗过判别器网络，欺骗的方式是生成一些看起来十分逼真的图像；同时第二个玩家判别器网络，试图把真实图片和虚假图片区别开，判别器试图正确指出哪些样本是生成器网络生成的。

在GAN模型中，需要从一个复杂的高维训练分布中采样，从这样的分布中生成样本，但是并没有可以直接实现的方式，解决方法是从一个简单分布中采样，比如符合高斯分布的噪声，然后学习一个从这些简单分布转换到我们想要的训练分布的一个变换，这个转换的过程需要利用神经网络来实现。

我们需要做的是取得一些具有某一指定维度的噪声向量作为输入，然后把该向量传给一个生成器网络，之后我们要从训练分布中采样并将结果直接作为输出。对于每一个随机噪声输入，都想让它与来自训练分布的样本一一对应。

下面简单介绍其训练过程：
GAN的训练过程就是上面提到的两个玩家的博弈过程，即生成器网络和判别器网络。

首先将随机噪声输入到生成器网络，生成器网络将会生成图片，将其称之为来自生成器的伪样本，然后从训练集中取一些真实图片，使用判别器网络对每个图片样本做出正确的区分，这是真实样本还是伪样本。

那么训练过程就是让生成器不断提高“造假”能力，让判别器不断提高“鉴赏”能力

通过一个mini max博弈公式训练这两个网络

公式如上，其中${\theta }_d$是判别器参数，${\theta }_g$是生成器的参数，训练目标是让目标函数在${\theta }_g$上取得最小值，同时在${\theta }_d$上取得最大值。

公式主体的第一项是在训练数据的分布上$log(D_{{\theta }_d}(x))$的期望，$log(D_{{\theta }_d}(x))$是判别器网络在输入为真实数据（训练数据）时的输出，该输出是真实数据从分布$p_{data}$中采样的似然概率；

第二项是对z取期望，z是从$p(z)$中采样获得的，这意味着从生成器网络中采样，同时$D_{{\theta }_d}(G_{{\theta }_g}(z))$这一项代表了以生成的伪数据为输入判别器网路的输出，也就是判别器网络对于生成网络生成的数据给出的判定结果。

训练目标：
判别器的目的是最大化目标函数也就是在${\theta }_d$上取最大值，这样一来$D_{{\theta }_d}(x)$就会接近1，也就是使判别结果接近真，因而该值对于真实数据应该相当高，相应地$D_{{\theta }_d}(G_{{\theta }_g}(z))$的值也就是判别器对伪造数据输出就会相应减小，我们希望这一值接近于0。因此如果能最大化这一结果，就意味着判别器能够很好的区别真实数据和伪造数据。对于生成器来说，我们希望它最小化该目标函数，也就是让$D_{{\theta }_d}(G_{{\theta }_g}(z))$接近1，如果$D_{{\theta }_d}(G_{{\theta }_g}(z))$接近1，那么用1减去它就会很小，判别器网络就会把伪造数据视为真实数据，也就意味着生成器在生成与真实样本非常相似的数据。

对于GAN的梯度计算和训练过程中的调整方法，这里不再涉及。

两篇参考：

1. GAN的原理入门
2. 理解GAN网络基本原理

GAN总结

• GAN不使用显式的密度函数，而是利用样本来隐式表达该函数，GAN通过一种博弈的方法来训练，通过两个玩家的博弈从训练数据的分布中学会生成数据。

• GAN可以生成目前最好的样本，还可以做很多其他的事情。但是不好训练且不稳定，这并不是直接优化目标函数，而是努力地平衡两个网络。

总结

通过本课程对生成模型有了初步的了解，但对于其中更深层次的概念和原理理解尚浅，很多东西现在的知识层次无法理解和明白，今后还需努力。

本文主要参考：
生成模型（PixelRNN/PixelCNN，变分自编码器，生成对抗网络）