激光SLAM论文阅读

[1] DL_SLAM: Direct 2.5D LiDAR SLAM for Autonomous Driving

主要工作——2019 IEEE Intelligent Vehicles Symposium (IV)

1. 基于2D占据栅格的SLAM方法有很多，GMapping， HectorSLAM and cartographer。但是2D-SLAM都会非常依赖于周围的障碍物，比如墙壁等等，因此不适用于室外场景。
2. 计算量大是3D-SLAM的普遍问题，实时建图难度很大。特征提取的方式可以一定成都上减少点云匹配的计算量，但容易受环境影响，比如树木等等。
3. 《DLO: direct lidar odometry for 2.5d outdoor environment》使用2.5D地图进行匹配，比ICP和基于特征的匹配速度都要快。问题：2.5D地图不能有效地应用于回环，因为直接的匹配方法受初始参数影响大。
4. 本文提出从2.5D高度图中提取segment features并将基于2.5D segment的闭环集成到DLO。
   • 基于2.5D图中segment features的快速回环检测。
   • 结合回环和图优化将DLO方法扩展成实时的SLAM系统。
   • 在KITTI数据集上验证了DL-SLAM要优于DLO和LOAM。

具体实现方法

前端

$$(x_i,y_i,z_i)=>(r_i,c_i,h_i)$$
$$r_i=x_i/f_x+c_x{c}_i=y_i/f_y+c_y{h}_i=z_i$$

参数代表栅格的分辨率和汽车中心位置的坐标。点云的高度期望用高度的平均值表示，梯度计算如下。
$$grad(q_i{)}_i^r=\mu (q_i{)}_i^{r+1}-\mu (q_i{)}_i^r$$

$$grad(q_i{)}_i^c=\mu (q_i{)}_i^{c+1}-\mu (q_i{)}_i^c$$

匹配方法

栅格化之后，直接匹配。假设障碍物的高度是不变的，height difference error(HDE):
$$e_i^k=z_i^k-\mu (m(T_i\ast p_{i-1}){)}_i^k$$
将第i-1帧点经过坐标变换和投影，计算第k个栅格的高度平均值，与第i帧的同一栅格的差值，表示为HDE。

最小二乘问题，优化的参数为T，优化的目标函数如下
$$J_i=\sum _{k\in C}{e}_i^k(T_i{)}^T\Omega e_i^k(T_i)$$
C表示第i帧所有栅格构成的集合，omega表示误差的协方差矩阵的逆矩阵。

误差对李代数求偏导的雅克比矩阵：
$$J_i^k=\frac{\delta e_i^k}{\delta {\xi }_i}=-\frac{\delta {\mu }_i}{\delta q_i}\frac{\delta q_i}{\delta p_i}\frac{\delta p_i}{\delta {\xi }_i}$$
三者分别表示栅格的梯度、3D空间投影到栅格的偏导、3D点对李代数的偏导。

最后通过高斯牛顿方法求解最小二乘问题。

基于2.5D segments的回环

segment

2.5D地图的直接匹配不能应用于回环检测和优化，因为这要求一个比较准确的初值。

本文从2.5D地图中提取segments来实现回环。

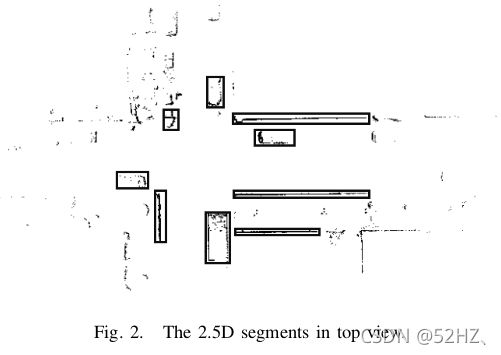
在本文中，每个segment有五种描述，principal direction, height gradient, curvature, omni-variance and eigen entropy。

• principal direction: PCA算法计算每个segment的rch(row, column, height)的均值和协方差矩阵，求协方差矩阵的特征值和特征向量。
• height gradient: 相邻栅格高度期望的差值。
• curvature: 翻译过来是表面偏差。

$$cr=\frac{{\lambda }_3}{{\lambda }_1+{\lambda }_2+{\lambda }_3}/cre$$

• omni-cariance: 表示数据的分散程度。

$$ov=({\lambda }_1{\lambda }_2{\lambda }_3{)}^{1/3}/ove$$

• eigen entrophy: 由特征值和阈值计算得出。

$$ee=({\lambda }_{1}log({\lambda }_1)+{\lambda }_{2}log({\lambda }_2)+{\lambda }_{3}log({\lambda }_3))/eee$$

因此，每个栅格有一个多维向量用于回环检测。
$$f=(v_1^T,v_2^T,v_3^T,h{g}^T,cr,ov,ee)$$

回环检测

回环检测的方法，用一个评价函数进行打分，计算segment特征向量的欧几里得距离：
$$scor{e}_{ij}=\sum _{k=1}^m(f_i(k)-f_j(k){)}^2$$
预先设置一个得分阈值和时间差阈值来进行回环检测额，得分小于一定值并且两帧之间的时间差足够大即认为检测到回环。

图优化

使用g2o 构建位姿图，以HDE为约束边，以位姿为顶点。
$$J_i=\sum _{k\in C}{e}_i^k(x_i,p_{i-1},p_i{)}^T\Omega e_i^k(x_i,p_{i-1},p_i)$$
假设在$x_i$和$x_j$之间检测到回环，误差函数：
$$J_{ir}=e_i^r(x_i,p_i,p_j{)}^{T}R{e}_i^r(x_i,p_i,p_j)$$
最终优化的目标函数为：
$$x_i^{\ast }=argmi{n}_{x_i}(J_{ir}+J_i)$$

实验结果

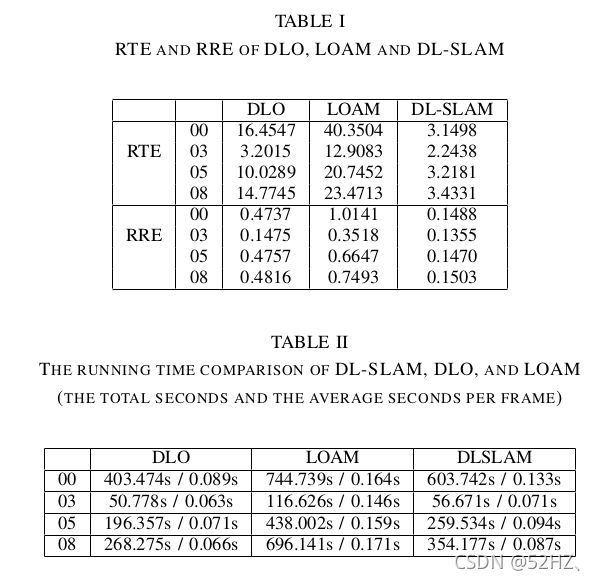
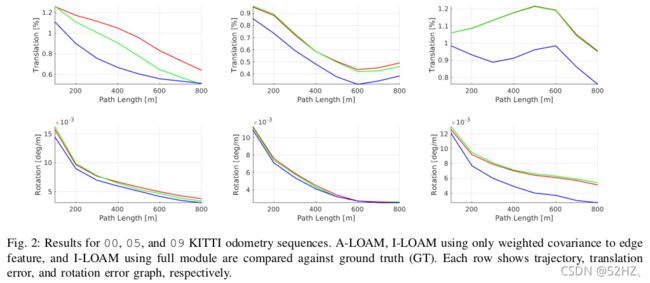
全程使用无IMU校正的Velodyne数据。在KITTI数据集上的表现要由于DLO和LOAM。

三种SLAM方法KITTI轨迹的比较。

三种SLAM方法误差比较（6Dof）。

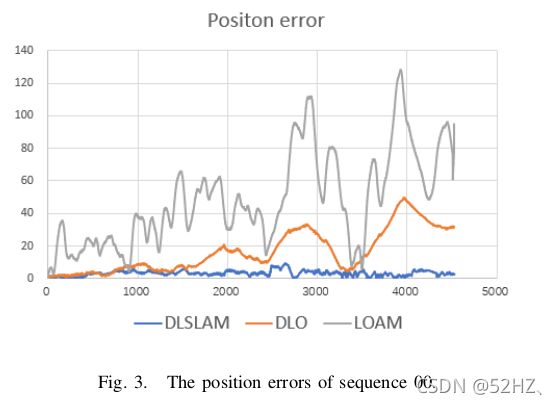
整体误差比DLO和LOAM小很多，运行时间比LOAM少，比DLO稍长。

总结

• 本文提出了一种基于2.5D高度图的直接LiDAR SLAM算法。
• 2.5D图中有多维信息用于回环，室内和室外环境的SLAM都可以进行。
• 前端采用直接法，后端采用基于2.5D segments特征的回环方法。

改进：

• 不能扩展到动态场景，动态场景中高度不变的假设不成立。
• 使用数据驱动的方法增强2.5D高度图的鲁棒性。

理解和思考

• 既然匹配的方法是投影栅格化之后直接匹配，肯定是基于汽车在同一个平面内运动的假设，不会匹配出roll、pitch和z变换，适用场景有限。
• 前端使用直接2D匹配的效果应该一般，更多的通过后端优化，能不能在前端匹配的时候就引入一些特征，增强前端匹配的准确度。目前只有高度误差函数作为匹配的依据，最好把高度分布作为优化函数的一部分。
• 在segment的特征部分，本文使用同一行或同一列相邻栅格的高度期望的差值来作为一个特征维度，但是每个栅格的高度具有偶然性，栅格越密集，梯度计算偶然数据的影响更大。所以在本文的基础上还可以在投影之前去除离群点，在计算梯度时综合考虑临近栅格和次临近栅格的高度差，这样的特征提取是不是更鲁棒。
• 本文用cr，ov，ee共同表示segment内点的分布情况，三者作为独立的维度，用三个阈值控制三者的权重。在面特征比较多的时候，curvature比omni-cariance更具有代表性，在点比较离散的时候后者应该更具有代表性。
• segment特征中没有考虑到几何特征（比如线、面），如果一个栅格内有多个面，只能通过点分布情况来保留特征，并没有面的检测。
• segment只有矩形，对场景的描述能力有限，可以考虑加入多边形和圆形，增强对某些特征的描述能力。

[2] SKD: Keypoint Detection for Point Clouds using Saliency Estimation

主要工作——2021 IEEE Robotics and Automation Letters (RA-L) + IEEE International Conference on Robotics and Automation (ICRA) presentation option

• 提出了一种利用显著性的关键点检测方法，该方法基于可微分描述子的梯度响应和场景的几何特征。

• 因为使用的是梯度响应而不是真实点，SKD对不同场景的鲁棒性强，在更换场景后不用重新训练网络。

• 在Oxford和KITTI的数据集的表现，两倍的匹配准确率和140%的相对重复率。（重复率：在同一场景的不同观测时，提取出相同关键点的能力）

具体实现方法

点云显著性

给出原始点云和一个预训练特征描述网络，从该网络的特定的一层提取出梯度。规定该层和该层梯度的乘积为显著性。
$$S(P)=F_l^P.▽F_l^P$$
理解：特定位置的梯度较大，说明该位置的点云特征性更强，在前端更容易被匹配。

上图可以看出，从中心到四周的点云密度不同，对不同密度进行补偿。

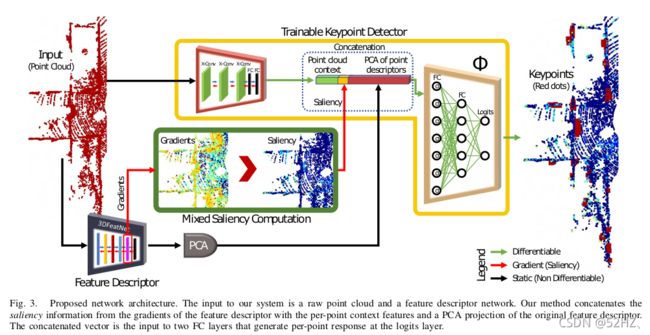
网络结构

本文设计了一个网络可以综合三个模块：

1. 点云的显著性。

2. PCA降维产生更平滑的特征，可以改善最终的结果。

3. point cloud context 4个卷积层和2个全连接层。

实验效果

精度更优，重复性更好。

理解和思考

• 使用本文方法提取出的key points会送到前端进行匹配，仍然要使用ICP或者NDT，并不是LOAM的匹配方法。神经网络在提取特征方面具有优势，所以很容易想到用神经网络来处理点云，更进一步可以引入注意力机制分析点与点之间的相关性，显然相关性强的点作为匹配的目标更可靠。
• 对于凹凸的墙角，在LOAM中统称为角点，通过计算角点到平面的距离和平面到平面的距离来进行点云的匹配。墙角的提取：两个平面的交线的一定垂直范围内刚好有一组角点存在，就认为这是一个墙角。墙角用一个方向向量和两个法向量表示，通过计算纵轴之间的距离，和另外两组向量的夹角，就能确定两帧之间雷达的位姿变换。

[3] Lightweight 3-D Localization and Mapping for Solid-State LiDAR

背景介绍——2021 IEEE ROBOTICS AND AUTOMATION LETTERS

• 固态激光点数更多，更新频率更快，FoV小，因此对算法的计算效率和鲁棒性要求更高。
• Another challenge is the pyramid-like coverage view that can cause severe tracking loss during large rotation.（另一个挑战是金字塔状的覆盖视图，在大旋转期间会导致严重的跟踪损失。）

主要工作

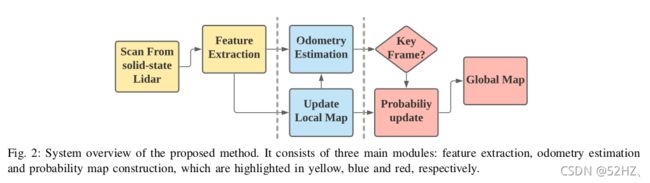
• 本文针对固态激光雷达提出一中轻量化的SLAM框架，包括三个部分：feature extraction, odometry estimation, and probability map building
• 利用水平曲率和垂直曲率提出了一种新的具有旋转不变性的特征。实验环境：手持平台的实时建图（不用考虑运动畸变）。
• 实验验证SLAM算法的实时性和鲁棒性。

具体实现方法

Feature Extraction

1. 首先过滤那些靠近视场边缘的点，将3D点云投影为2D的矩阵。
2. 将视场划分为M*N个cell，每个cell呈锥形，计算每个cell所有点的几何中心$p_k^{(m,n)}$​，当cell足够小时，cell是一个面。
3. 计算$p_k^{(m,n)}$处的局部光滑度，公式如下，S表示$p_k^{(m,n)}$的一个邻域，$\lambda$​越大表示希望提取的特征点越多。

$${\sigma }_k^{(m,n)}=\frac{1}{{\lambda }^2}.\sum _{p_k^{(i,j)}\in S_k^{(m,n)}}(||p_k^{(i,j)}||-||p_k^{(m,n)}||)$$

$$S_k^{(m,n)}=\{p_k^{(i,j)}|i\in [m-\lambda ,m-\lambda ],j\in [n-\lambda ,n+\lambda ]\}$$
${\sigma }_k^{(m,n)}$越大表示该点越锋利，为edge feature，反之为plane feature。

Odometry Estimation

1. 对于edge point，提取local map上的最临近两个点构成线，计算点到线的距离。
2. 对于planar point，计算点到面的距离，类似LeGO-LOAM。
3. 两种距离之和作为非线性优化的目标函数，使用优化方法left perturbation scheme and apply increment on Lie Group，左扰动方案并在李群上应用增量，这部分有很多公式推导。但核心仍然是求解一个非线性最小二乘问题，优化的参数是旋转矩阵R和平移向量t。
4. 优点：
   • 旋转矩阵或者位姿以无奇点格式存储
   • 在每次迭代中执行无约束优化
   • 操作的对象是矩阵，因此没有容易出错的对标量三角函数求导的过程
5. 比较准确的初值也能加速此方法的迭代，本文使用了类似RenQian的位姿推测，使用前两帧的位姿，假设汽车保持运动状态不变。

$$T_k^0=T_{k-1}.T_{k-2}^{k-1}=T_{k-1}.T_{k-2}^{-1}.T_{k-1}$$

Probility Map Construction

1. 使用关键帧进行全局地图的更新，使用octree加速查找。

2. 概率更新公式：$P(n|z_{1:t})={[1+\frac{1-P(n|z_t)}{P(n|z_t)}.\frac{1-P(n|z_{1:t})}{P(n|z_{1:t})}.\frac{P(n)}{1-P(n)}]}^{-1}$

实验结果

理解和思考

1. 本文仍然是提取edge point和planar point，然后求解点到线的距离和点到面的距离来进行scan-to-map。与LOAM不同的是，本文计算粗糙度的方法不一样，先过滤离群点，然后将视场投影，再计算cell的粗糙度。本来以为论文里面说是邻域，以为是不仅仅考虑同一条扫描线的点，也会把相邻线的相邻点加到粗糙度的计算步骤，但是看过论文之后，发现不然。粗糙度的计算和LOAM一样。
2. 投影栅格化之后，每个cell可能会含有多个面特征，要想避免这种情况，就要使用更加稠密的栅格，会增加计算的负担。
3. 根据关键帧构建概率地图，并给出了概率地图的更新公式，算是一个创新。
4. 由本文的粗糙度计算方法想到一种提取凹点和凸点的方法，在提取出edge point之后，考虑该点的一个邻域，求邻域内所有点的几何中心，该点和几何中心构成的向量方向可以确定该edge point的凹凸性。

[4] ROI-cloud: A Key Region Extraction Method for LiDAR Odometry and Localization

主要工作——2020 IEEE International Conference on Robotics and Automation (ICRA)

• 提取由高概率立方体组成的关键区域，通过利用历史信息和提取几何特征来有效去除冗余和动态点云。

• 使用无参数滤波器精确有效地近似关键区域的分布。

• 验证ROI点云和多种主流的雷达里程计和基于地图的定位，实验表明该方法可在密集的城市环境中实现更好的准确性和速度。

具体实现方法

System Overview

1. 输入：原始点云数据和IMU数据。

   输出：目标点云（ROI-cloud）。

2. 最新的雷达扫描经过一个快速的特征提取模块，将提取出的特征作为当前的观测。

   同时，在贝叶斯滤波的框架中，前一时间步长的粒子分布包含先验信息，并结合IMU/里程计预测当前的ROI。

3. 预测的ROI经过重采样和蒙特卡洛采样作为输出的点云。

Feature Extraction

1. 假设机器人很少发生roll和pitch的变化，提取出地面点。

2. 计算点的几何光滑度，（考虑同一条扫描线的前后几个点）：
   $${\xi }_i=\frac{1}{|S_i|.||p_i^l||}.||\sum _{j\in S_i,j\ne i}(p_j^l-p_i^l)||$$
   对得到的光滑度取对数得到一条新的分布曲线，从曲线的左边开始搜索edge point和planar point，取代LeGO-LOAM中排序算法，复杂度明显降低。

3. 将特征点云栅格化，求每个栅格内所有点的协方差矩阵，对协方差矩阵进行特征值分解求得三个特征值，如下公式计算此cube的重要性：
   $$f_{ck}=\frac{{\lambda }_1^e}{{\sum }_{j\in {\sum }^e}{\lambda }_j^e}|P_{c_k}^e|+\eta \frac{{\lambda }_1^p+{\lambda }_2^p}{{\sum }_{j\in {\sum }^e}{\lambda }_j^e}|P_{c_k}^p|$$

4. $|P_{c_k}^e|$表示cube内边特征的个数，$|P_{c_k}^p|$表示cube内面特征的个数，$\eta$是边特征和面特征之间的平衡因子。

Importance updating

1. cube的重要性通过应用粒子滤波器进行更新，每个粒子代表cube的特定位置。

2. ROI-cloud的初始分布是通过在整个3D空间上随机均匀绘制的一组粒子。随着新测量的到来，粒子将逐渐在关键区域附近积累。因为每一次更新都会综合考虑上一帧的粒子分布和当前帧的观测，所以对于动态的障碍物比较好过滤，论文中讲了很多统计学的应用，读起来比较吃力。

3. 最后，重采样将统一的权重重新分配给粒子集，然后增加靠近关键区域的粒子数目，使这些立方体成为高概率。

Other Details

1. 粒子容易聚集在几个旧的关键区域上，不能随着机器人的移动及时发现新的关键区域。 因此，只使用80%-90%粒子进行重采样，而其余部分在lidar观测端随机插入，这样对于比较旧的ROI就会逐渐消散。
2. 为了在环境中均匀分布关键区域，将 360 度视角分成四个相同的子区域，并在每个子区域中分别应用贝叶斯滤波器框架。否则，里程计很容易漂移，定位精度会下降。
3. 在更新过程中，对区域的概率设置一个阈值，避免此处的概率过大，造成整个粒子集的退化。
4. 提取处ROI-cloud之后，使用ROI-cloud充当特征点云在雷达里程计、建图、定位模块中使用。

实验结果

初始时，粒子是均匀分布的。1s内，收到10帧扫描数据，粒子在关键区域聚集。显然，粒子的数目会影响提取ROI-cloud的时间，而且粒子过多灰造成不应该的区域被关注，因此应使用适当是粒子数目。

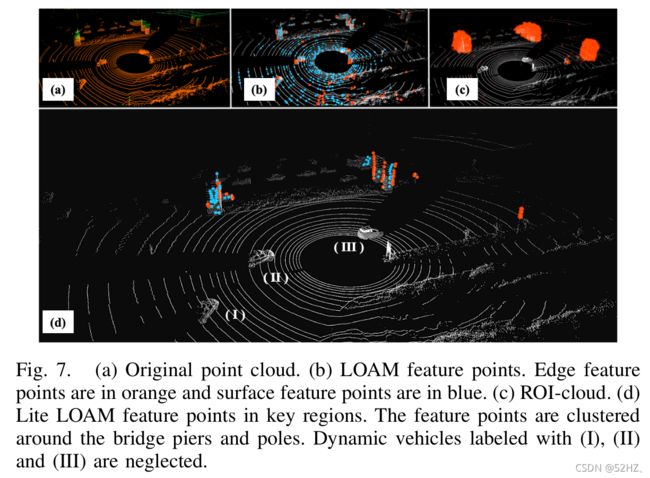
可以看出有些类似语义分割的效果，但实际上并没有语义信息被识别，贝叶斯框架只是判断出这个区域有更多的特征信息。使用ROI-cloud之后，NDT匹配时间减少72.35%，位姿误差减小7.65%。

在作者自行收集的数据集上的效果好到离谱，不太可信。

理解和思考

1. 本文的特征提取的方法与LeGO-LOAM基本一致，只是在提取特征的过程中，系统始终维护着一个粒子集，这个粒子集代表着哪些区域是更加关键的区域，结合粒子集和特征点云经过蒙特卡洛采样给出最终参与匹配的目标点云。有类似语义分割的效果，但是并没有使用神经网络，作者特地在文中吹了这一点。
2. 在传统的特征点云提取出来之后，应用贝叶斯滤波框架（有轮速编码器或者IMU信息），是其他论文里没见过的，是一个创新点。贝叶斯框架不仅能筛选出具有更多特征的点云，还能过滤掉动态障碍物，因为框架中包含了历史的位姿信息。

[5] 6-DOF Localization in 3D Feature Points Maps for LiDARs of Small FoV

主要工作——2021 5th International Conference on Robotics and Automation Sciences

1. 提出了一种轻量化的固态激光雷达建图和重定位方法。
2. 解决了小FoV激光雷达突然转向的匹配漂移问题。
3. 提出了一种基于特征点地图的、可实时运行的、轻量化高精度重定位方法。

具体实现方法

Feature Extration

Map generation部分使用LOAM框架，特征提取的方式与LOAM一致，在匹配方法上有一个改进，解决了小FoV激光雷达突然转向的匹配漂移问题。

Pose Estimation

1. 假设所有扫描到的对象在一定范围内都看成是一个面。对于边特征，首先在global map上寻找与其最近的五个edge point，计算五个点的协方差矩阵，只要最大的特征值比第二大的特征值大三倍，这五个edge point就被认为是共线的。（类似PCA主成分分析）
   $$m=\frac{(P_s-P_1^e)\times (P_s-P_2^e)}{|P_s^e-P_1^e|.|P_s^e-P_2^e|}$$

   $$n=\frac{(P_s-P_2^e)\times (P_s-P_5^e)}{|P_s^e-P_2^e|.|P_s^e-P_5^e|}$$

   m, n分别是经过$P_s,P_1^e,P_2^e$​和$P_s,P_1^e,P_2^e$​平面的法向量，优化目标函数：
   $$r_e=\frac{m\times n}{m\cdot n}$$

2. 对于面特征，同样是计算五个最邻近点的协方差矩阵，如果最小的特征值小于第二小特征值的三分之一，就认为五点共面，优化目标函数：
   $$r_p=\frac{(P_S-P_1^l{)}^T((P_3^l-P_5^l)\times (P_3^l-P_1^l))}{|(P_3^l-P_5^l)\times (P_3^l-P_1^l)|}$$

3. 最后的目标函数为所有edge point和planar point的$r_e$和$r_p$之和。

Relocalization

重定位使用的是LOAM中的特征点匹配的方式：

不同点：在目标函数里面加入了权重，权重的计算运用到了intensity，强度越大的点在优化时权重越大：
$$W_i=s\cdot exp(-\sum _{i=1}^c\frac{|I(P_i)-I(P_O)|}{I_{ave}})$$

实验结果

转弯时的轨迹预测不会漂移，因为FoV很小，Loam_Livox容易发生漂移。

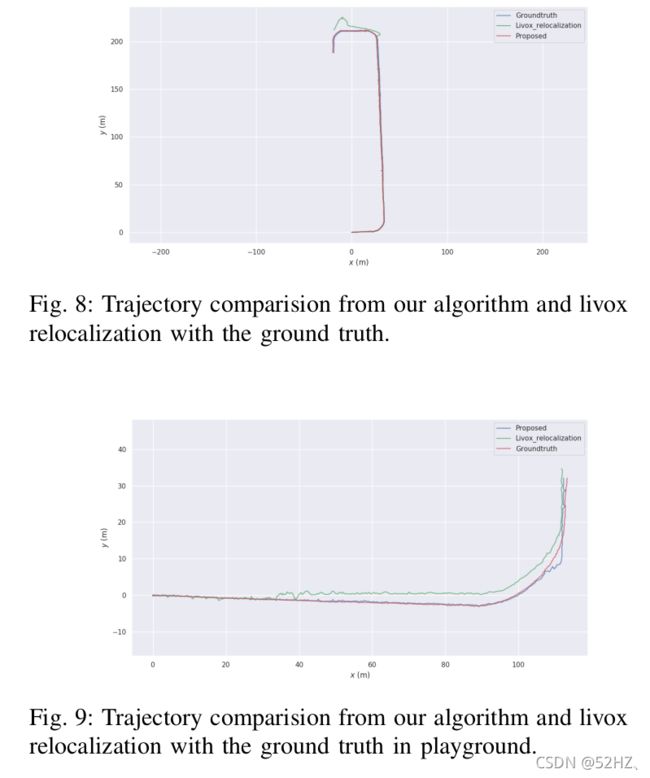
和Livox_Loam比较，重定位的误差小。

理解和思考

1. 在位姿预测部分，对于面特征，计算的还是距离，而对于线特征，$r_e$​的物理意义不清楚。重定位部分与LOAM的区别只有是否加权的区别，为什么本文不会产生漂移。

2. 在LOAM的雷达里程计部分，对于特征匹配的两种特征也可以使用强度来加权。（下文就是针对这个）

[6] I-LOAM: Intensity Enhanced LiDAR Odometry and Mapping

主要工作——2020 17th International Conference on Ubiquitous Robots (UR)

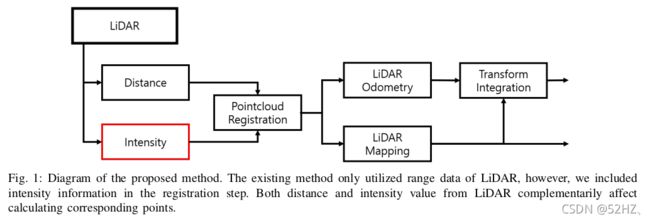
1. 在特征提取的时候把强度信息加入。相对于LOAM，本文使用了新的特征匹配目标函数。
2. 在KITTI上验证了对于其他LOAM的优越性。

具体实现方法

1. 使用A-LOAM框架，不同点只有点云匹配。

LiDAR odometry with intensity

$$d_i=\sqrt{(X_i-X^L{)}^T(X_i-X^L)}$$

$$d_i^I=||I_i-\bar{I}||$$

$$w_i^o=e^{-(d_i+d_i^I)}$$

LiDAR mapping with intensity

相邻的有相同强度的点被设置更高的权重，更有可能成为特征点，在优化时也具有更大的权重。
$$w_i^m=ex{p}^{-||I_i-\bar{I}||}$$
协方差矩阵：
$$M^{\ast }=\frac{1}{{\sum }_{i=1}^N}{w}_i^m((X_i-\bar{X}{)}^T(X_i-\bar{X}))$$
优化目标函数：
$$argmi{n}_{\beta }\sum _{i=1}^m{w}_i^m|y_i-\sum _{j=1}^n{x}_{ij}{\beta }_j{|}^2$$

实验结果

位姿误差减少，系统运行时间减少，但是不明显。

理解和思考

1. 因为强度一样的点更有可能是同一组特征点，本文就是简单的用强度给特征点加权，并没有提取新的特征类型。能不能在点云中提取新的特征类型，至少将凸点和凹点区分开，通过计算帧上凸点与地图上最近邻凸点的距离来优化匹配。
2. 显然强度相近的点更容易表示同一个事物，因此聚类时可以将强度考虑进来。

[7] A Line/Plane Feature-based Lidar Inertial Odometry and Mapping

主要工作——2019 Chinese Control Conference (CCC)

1. LOAM主要是通过计算局部的粗糙度来提取边和平面特征，这在一些杂乱的环境中是不可靠的，本文对特征提取模块做了改进。

具体实现方法

本文是一个经典带回环检测的LOAM框架，高频里程计和低频建图。

Feature Extraction

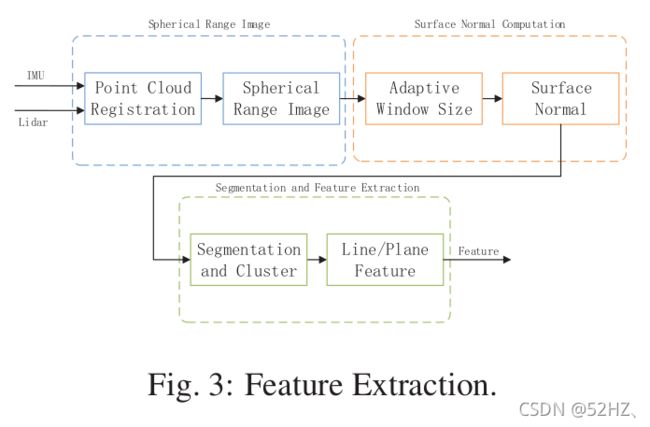
每一帧雷达扫描数据都经过IMU预匹配，然后投影到球体距离图（Spherical Range）上，由球体坐标系定义，转换公式：
$$\left[\begin{array}{c}r\\ \theta \\ \varphi \end{array}\right]=\left[\begin{array}{c}\sqrt{x^2+y^2+z^2}\\ arctan(x/z)\\ arcsin(y/\sqrt{x^2+y^2+z^2})\end{array}\right]$$
表面法向量计算。常用的计算表面法向量的方法是整体线性最小二乘法，但是会非常消耗计算资源。本文采用的方法是先用一个小矩形窗口确定临近点，然后用临近点预测每个点的法向量。

求球坐标系下的全微分：
$$\Delta =x(\frac{\partial }{\partial r}sin\theta cos\varphi +\frac{\partial }{\partial \theta }\frac{cos\theta }{rcos\varphi }-\frac{\partial }{\partial \varphi }\frac{sin\theta sin\varphi }{r})+y(\frac{\partial }{\partial r}sin\varphi +\frac{\partial }{\partial \varphi }\frac{cos\varphi }{r})+z(\frac{\partial }{\partial r}cos\theta cos\varphi +\frac{\partial }{\partial \theta }\frac{sin\theta }{rcos\varphi }-\frac{\partial }{\partial \varphi }\frac{cos\theta sin\varphi }{r})$$
SRI面方程为$r=s(\theta ,\varphi )$，应用全微分可求得法向量为：
$$n=\Delta s(\theta ,\varphi )=[zxy]R_{\theta ,\varphi }\left[\begin{array}{c}1\\ \frac{1}{rcos\varphi }\frac{\partial r}{\partial \theta }\\ \frac{q}{r}\frac{\partial r}{\partial \varphi }\end{array}\right]$$
$R_{\theta ,\varphi }$​​​​​是方位角和俯仰角的旋转矩阵，可提前计算得到。偏导数是通过在SRI上应用标准图像处理卷积核获得的（这通常用于图像中的边缘提取），然后应用Prewitt算子。 至此，就计算出了每个点的法向量。

分割和特征提取。首先聚类获得点云簇，然后对每个簇运用主成分分析法来获取线特征和面特征。在聚类部分使用基于区域增长的方法，区域生长时的条件是生长点和种子的距离小于阈值，两个点对应的法向量夹角小于阈值，否则舍弃生长点，并且舍弃点数目过少的类。

聚类之后，对每个类运用PCA算法，计算每个类的协方差矩阵，求解特征值和特征向量，判断特征值的大小关系就能确定类是否属于边特征或者面特征。

结合特征向量确定拟合直线或者平面，最终满足一下条件的特征才能留下：
$$边特征：\frac{{\lambda }_1^c+{\lambda }_2^c}{{\lambda }_1^c+{\lambda }_2^c+{\lambda }_3^c}<{ϵ}_l,e=\frac{1}{|c_i|}\sum _{p_j\in c_i}d(L_i,p_j)<{ϵ}_{p2l}$$

$$面特征：\frac{{\lambda }_1^c+{\lambda }_2^c}{{\lambda }_1^c+{\lambda }_2^c+{\lambda }_3^c}<{ϵ}_l,e=\frac{1}{|c_i|}\sum _{p_j\in c_i}d(L_i,p_j)<{ϵ}_{p2l}$$

至此，就是特征提取的全步骤，效果如下：

Lidar Odometry and Mapping

在高频雷达里程计部分，同样是计算点到线的距离和点到面的距离来构造一个非线性最小二乘问题，本文再用了LM优化方法。

在建图部分，本文采用和LEGO-LOAM一样的方法，构建关键帧地图减小计算的压力，并且构建位姿图进行优化。

实验结果

LOAM易受环境中草和树叶的影响，本文的方法不会。

回环检测也比较准确。

理解和思考

1. 本文对标的是LOAM，最大的改进在于特征提取部分，不像是LOAM中简单的计算曲率的方式，本文的方法更加可靠。另外还加入了回环检测，控制累计误差在一定范围内。
2. 本文在特征提取是没有提地面点，而且没有给出在公开数据集（比如KITTI）上的效果，以及和LEGO-LOAM的准确率比较，应该是准确率不及LEGO-LOAM。但是本文新颖特征提取的方式是一个启发，使用法向量来作为聚类的依据，并且投影到球坐标系加速法向量的计算。

A Fast and Accurate Planar-Feature-Based Global Scan Registration Method

主要工作

1. 经典的点云匹配方法ICP、NDT都需要一个较为准确的初值，没有IMU这是很难做到的，因此本文给出一个基于平面特征的点云匹配方法。

2. 本文推到了一种考虑了传感器噪声模型的基于修正重整化的算法，并将其用于精确的平面拟合和协方差计算。

3. 使用了基于体素增长的有效的平面分割算法来提取平面特征。

4. 使用了一种新颖的基于投影图像的快速平面属性计算，并且利用单个平面的属性和平面之间的约束进行匹配。

5. 针对数据集研究了归一化和不同变换估计方法对扫描配准精度的影响。

具体实现方法

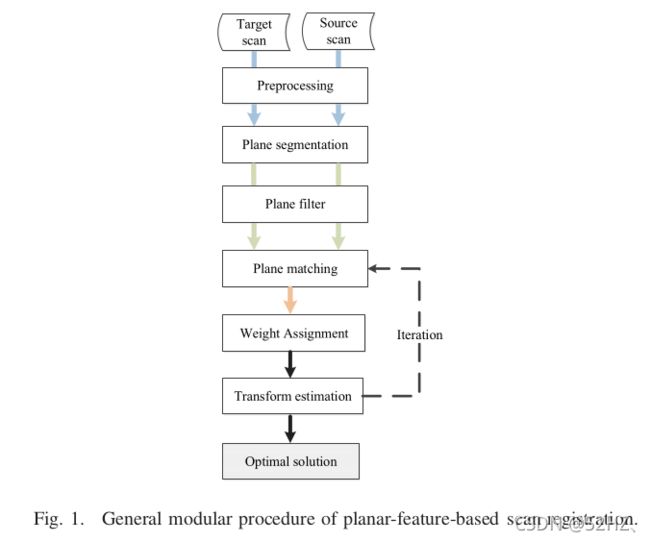
首先通过滤波、光滑、下采样以及其他预处理。然后经过平面分割，得到很多平面片。对平面片进行过滤，保留下适合进行匹配的平面片。最后就是加权和位姿预测。

Preliminaries

1. 首先假设激光雷达对角度的测量比距离测量要准确，也就是噪声主要在测量距离$\rho$​，而点的方向向量$\tilde{m}$​较为准确。第二个假设高斯噪声:
   $${\rho }_j\sim N\{\widetilde{{\rho }_j},{\sigma }^2\{\widetilde{{\rho }_j}\}\}$$

$$\widetilde{{\rho }_j}=d/n\cdot \tilde{m}$$

本文有大段的理论公式推导，实在理解困难，就此作罢。

以上均为本人的个人理解，若有错误，欢迎斧正。