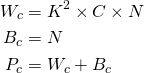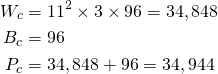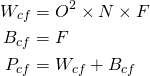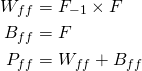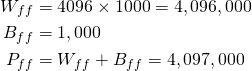一个卷积神经网络(CNN)中包含的张量大小和参数个数的计算
本篇文章来自于learnopencv.com/number-of-parameters-and-tensor-sizes-in-convolutional-neural-network/，感谢原作者的详细讲解。本人增加一些白话进行补充说明，高手请绕行。~-~
在这篇文章中，我们分享了一些公式来计算张量（图像）的大小和卷积神经网络（CNN）中每一层的参数个数。 此帖子不定义CNN中使用的基本术语，并假定您熟悉它们。在这篇文章中，Tensor一词仅仅是指具有任意数量通道的图像。 我们将以AlexNet为例展示计算结果。因此，这里是AlexNet的架构，供参考。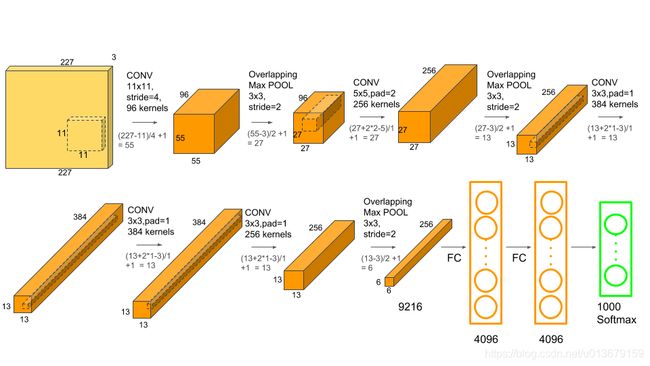
AlexNet有以下几层
1、输入层：大小为227x227x3的彩色图像。AlexNet的论文提到了224×224的输入大小，但这是论文中的一个书写错误。
2、卷积层1：由96个尺寸为11×11的卷积核组成，步长为4，填充为0。
3、最大池化层1：由3×3和步长2组成。
4、卷积层2：由256个大小为5×5的卷积核组成，步长为1，填充为2。
5、最大池化层2：由3×3和步长2组成。
6、卷积层3：由384个大小为3×3的卷积核组成，步长为1，填充为1。
7、卷积层4：卷积层4与卷积层3具有相同的结构。它由384个大小为3×3的内核组成，步长为1，填充为1。
8、卷积层5：由256个大小为3×3的内核组成，步长为1，填充为1。
9、最大池化层3：由3×3和步长2组成。
10、全连接层1：第一个完全连接层有4096个神经元。
11、全连接层2：第二个完全连接层有4096个神经元。
12、全连接层3：第三个完全连接层有1000个神经元。
接下来，我们将用上面的架构来解释
1、如何计算每个阶段的张量大小
2、如何计算网络中的参数总数
卷积层输出张量（图像）的大小
我们来定义一下
O = 输出图像的大小（此处指宽度）
I = 输入图像的大小（此处指宽度）。
K = 卷积层中使用的卷积核的大小（此处指宽度）。
N = 卷积核个数。
S = 卷积运算的步长。
P = 填充个数。
输出图像的大小（O）由 下式确定：
![\[ O = \frac{I - K + 2P}{S} + 1 \]](http://img.e-com-net.com/image/info8/668057787985478cae6e73db506ada63.png){kind=small}
输出图像中的通道数等于该卷积层的卷积核个数N。
示例：
在AlexNet中，输入图像的大小为227x227x3。即宽为227，高为227，通道数为3。卷积层1有96个卷积核，每个卷积核的大小为11x11x3，步长为4，填充为0。因此，在卷积层1之后输出图像的大小（此处指宽度）是
![\[ O = \frac{ 227 - 11 + 2 \times 0 }{4} + 1 = 55 \]](http://img.e-com-net.com/image/info8/206d96f9046b46e8ad98cd75d46a8f6d.png){kind=small}
因此，输出图像的大小为55x55x96（每个卷积核生成一个通道）。 请读者使用上述图像作为指南来验证卷积层2、卷积层3、卷积层4和卷积层5的输出图像的大小。
Max Pool层输出张量（图像）的大小
我们来定义一下
O = 输出图像的大小（此处指宽度）。
I = 输入图像的大小（此处指宽度）。
S = 卷积运算的步长。
=池大小。
输出图像的大小（O）由下式确定
![\[ O = \frac{ I - P_s }{S} + 1 \]](http://img.e-com-net.com/image/info8/b5fb63764d0c49dbbc21652e260382ea.png){kind=small}
请注意，该公式可由上一节中卷积层输出图像大小的计算公式获得，只要使填充等于零，并且与卷积核大小K相同即可。但与卷积层不同的是，最大池化层输出的通道数不变。
例如：在AlexNet中，卷积层1之后的最大池化层的池大小为3，步长为2。我们从上一节中知道，这个阶段的图像是55x55x96。最大池化层1之后的输出图像大小（此处指宽度）
![\[ O = \frac{ 55 - 3 }{2} + 1 = 27 \]](http://img.e-com-net.com/image/info8/0691f7e212894f55ac16b874fd6c96f2.png){kind=small}
因此，输出图像的大小为27x27x96。 我们留给读者来验证最大池化层2和最大池化层3输出的大小。
完全连接层输出的大小
一个完全连接层输出一个向量，该向量长度（向量的元素个数）等于层中的神经元个数。
总结：AlexNet各个层的张量大小 （即每个层的神经元个数）
在AlexNet中，输入是一个大小为227x227x3的图像。在卷积层1之后，将变为为55x55x96的大小，在最大池化层1之后转换为27x27x96。在卷积层2之后，大小更改为27x27x256，并在最大池化层2之后更改为13x13x256。之后卷积层3将其转换为大小为13x13x384，而卷积层4则保持大小不变，卷积层5将更改大小为27x27x256。最后，最大池化层3将尺寸缩小到6x6x256。该图像输入全连接层1，将其转换为大小为4096×1的向量，接下来经过全连接层2，尺寸保持不变，最后，经过全连接层3之后的尺寸为1000×1。 接下来，我们要计算每个卷积层中的参数个数。
卷积层的参数个数
在CNN中，每一层都有两种参数：权重和偏差。参数的总数只是所有权重和偏差的总和。
我们来定义一下：
=Conv层的权重个数
=Conv层的偏差个数
=Conv层的参数个数
K=卷积层中使用的卷积核的大小（此处指宽度）
N=卷积核个数
C=该层输入图像的通道数
在卷积层中，每个卷积核的深度总是等于输入图像中的通道数。所以每个卷积核都有K^2 × C 个参数，并且有N个这样的卷积核。这就是我们得出上述公式的方法。
例如：在AlexNet中，在卷积层1中，输入图像的通道数（C）为3，卷积核大小（K）为11，卷积核数（N）为96。所以参数的个数是：
读者可以验证卷积层2、卷积层3、卷积层4、卷积层5的参数个数分别为614656、885120、1327488和884992。因此，卷积层的参数总数为3747200。你认为这是一个很大的数字？好吧，等到我们看到完全连接层，你就不会这么想了。卷积层的好处之一是，权重是共享的，因此我们的参数比我们在完全连接层的情况下要少的多。所谓权重共享的意思是，卷积层的输出结果中的每个通道由一个卷积核（仅1个）经过卷积运算获得，以卷积层1为例，它的输出为55*55*96，即共有96个通道，每个通道大小为55*55，具体到其中任意一个通道，比如第一个通道C1，由55*55个点组成，它是如何得到的呢？就是由相应的1号卷积核对输入图像（227*227*3）进行一次卷积运算得到的，生成的55*55里面的每个点所使用的权重参数都是这个1号卷积核，这就叫权重共享。
最大池化层的参数个数
没有与最大池化层相关联的参数。池的大小、步长和填充都是超参数。
全连接（FC）层的参数个数
在CNN中有两种完全连接的层。第一种是该全连接层的前面连接着最后一个卷积层，第二种是该全连接层的前面连接着其他全连接层。让我们分别考虑每一种情况。
情况1：前面连接着卷积层的全连接（FC）层的参数个数
我们来定义一下：
=连接到卷积层的全连接层的权重个数。
=连接到卷积层的全连接层的偏差个数。
O=前一个卷积层的输出图像的大小（宽度）。
N=前一个卷积层中的卷积核个数。
F=全连接层中的神经元个数。
示例：AlexNet的第一个全连接层连接到卷积层。对于这一层，O=6，N=256，F=4096。因此，
这一层的参数个数比所有卷积层的参数个数总和还要多！
情况2：前面连接着其它全连接层的全连接（FC）层的参数个数
我们来定义一下：
=全连接层的权数。
=全连接层的偏差数。
=全连接层的参数数目。
F=全连接层中的神经元数。
=前一个全连接层中的神经元数。
在上述公式中， × F是前一个全连接层到本全连接层的权重总数。偏差总数与本全连接层的神经元数（F）相同。
示例：AlexNet的最后一个全连接层连接到全连接层。对于这一层，=4096，F=1000。因此，
我们留给读者来验证AlexNet中全连接层2的参数总数为16,781,312。
AlexNet中参数和张量大小（神经元个数）的数目
在AlexNet中的参数总数是5个卷积层加3个全连接层中所有参数的总和。结果竟然是62378344！下表为摘要。
注：Conv ->卷积层，MaxPool -> 最大池化层， FC -> 全连接层
| Layer Name | Tensor Size | Weights | Biases | Parameters |
| Input Image | 227x227x3 | 0 | 0 | 0 |
| Conv-1 | 55x55x96 | 34,848 | 96 | 34,944 |
| MaxPool-1 | 27x27x96 | 0 | 0 | 0 |
| Conv-2 | 27x27x256 | 614,400 | 256 | 614,656 |
| MaxPool-2 | 13x13x256 | 0 | 0 | 0 |
| Conv-3 | 13x13x384 | 884,736 | 384 | 885,120 |
| Conv-4 | 13x13x384 | 1,327,104 | 384 | 1,327,488 |
| Conv-5 | 13x13x256 | 884,736 | 256 | 884,992 |
| MaxPool-3 | 6x6x256 | 0 | 0 | 0 |
| FC-1 | 4096×1 | 37,748,736 | 4,096 | 37,752,832 |
| FC-2 | 4096×1 | 16,777,216 | 4,096 | 16,781,312 |
| FC-3 | 1000×1 | 4,096,000 | 1,000 | 4,097,000 |
| Output | 1000×1 | 0 | 0 | 0 |
| Total | 62,378,344 |