3、k - 最近邻分类器及使用验证集取得超参数
3、k - 最近邻分类器
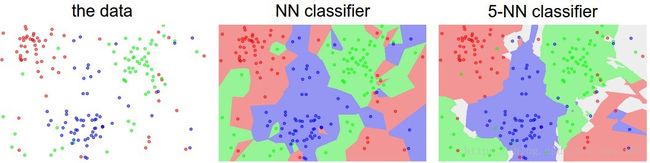
注意到了吗,前面我们做一个预测时,只使用最近的图像的标签。事实上,通过使用所谓的k-最近邻分类器可以做得更好。这个想法很简单:在训练集中,不是找到最接近的一个图像,而是找到最近的k个图像,并用这k个图像占多数的标签作为待预测图像的标签。特别地,当k=1时,就是前面的最近邻分类器。K取较高值具有平滑效果,使得分类器更能抵抗异常值:
最近邻居和5近邻分类器之间的差异的例子,使用二维点和3个分类(红色、蓝色、绿色)。有色区域显示由L2距离分类器画出的决策边界。白色区域显示不明确分类的点(该点可以被标记为至少两个类)。注意,在最近邻分类器的情况下,离群数据点(例如蓝色块中的绿点)创建了可能不正确预测的小岛,而5-NN分类器平滑这些不规则性,这样的话对测试数据具有更好泛化能力。
实践中,我们几乎总是希望使用k-最近邻。但是,K应该取多大的值?我们接着讨论这个问题。
调整超参数的验证集
K近邻分类器需要设置一个K,但要设置多大最有效呢?另外,我们发现可以使用很多不同的距离函数:L1范数,L2范数,还有很多我们甚至没有考虑过的选择(例如点积)。这些选择被称为超参数,它们经常出现在许多从数据中学习的机器学习算法的设计中。到低应该设置一个什么样的值/设置,总是不那么明显。
你可能会建议,我们应该尝试许多不同的值,看看哪个是最好的。这是一个好主意,这确实是我们将要做的,但这必须非常仔细地完成。特别是,我们不能使用测试集来调整超参数。每当你设计机器学习算法时,你应该把测试集看作一个非常宝贵的资源,直到最后一次才使用。否则就非常危险,调整得到的超参数在测试集上工作得很好,但是如果要部署模型,则可以看到性能明显降低。实际上,我们会说你在测试集上过拟合了。也可以这么理解,如果在测试集上调整超参数,那就是把测试集也当作训练集来使用了。因此,您所获得的模型评价性能将过于乐观,部署到实际应用中就不是那么回事了。但是如果只在结束时使用一次测试集,它仍然不失为衡量分类器泛化能力的一个很好的代理(我们将在以后的课堂上看到更多的关于泛化的讨论)。
只在最后,在测试集上对模型做一次评估
幸运的是,有一种调整超参数的正确方法,它根本不接触测试集。这个想法是把我们的训练集分成两个:一个作为更小的训练集,另外一个我们称之为验证集。以CIOWE10为例,我们可以使用49000张训练图像进行训练,并留出1000张用于验证。这个验证集就是被用作伪测试集来调整超参数的。
代码如下所示:
我们可以绘制一个图表,显示哪些k值工作最佳。然后,我们将使用这个值,并在测试集上进行一次评估。
将训练集分成训练集和验证集。使用验证集来尝试各种超参数。最后在测试集验证一次并报告性能。
交叉验证。在训练数据较少的情况下,有时会使用一种更复杂的技术来选择超参数,称为交叉验证。其想法是,就前述实例而言,不用随意挑选前1000个数据点作为验证集以及剩余的数据作为训练集,可以通过迭代不同的验证集来获得一个更好的k值。例如,在5倍交叉验证中,我们将训练数据分成5个相等的折叠,使用其中4折进行训练,1折叠进行验证。然后,我们交替使用其中4个折叠作为训练集,另外一个折叠作为验证集,得到5个准确率,最后取平均值。
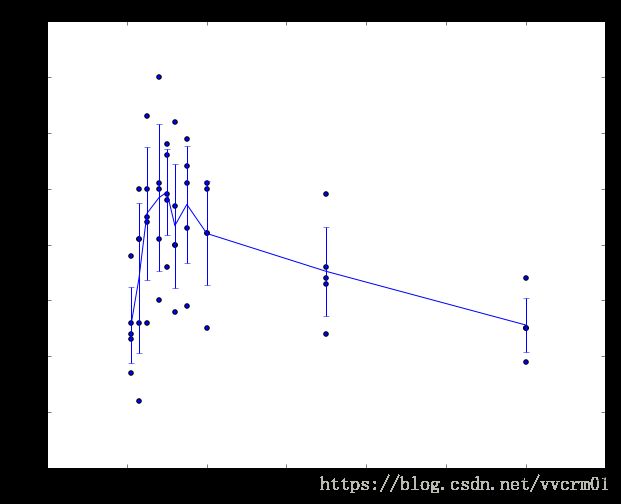
5折交叉验证取K值的例子。对于不同K值,循环用其中4个子训练集训练,用一个子集评估。因此,对于每个k,我们在验证子集上得到5个精度(精度是y轴,每个结果是一个点)。趋势线是通过每个K的结果的平均值绘制的,而误差条表示标准偏差。注意,此例中,交叉验证表明大约k=7的值是最佳的(对应于图中的峰值)。如果拆分数据的份数超过5,还可能得到到一个更加平滑(即较少噪音)的曲线。
但是实践中,人们倾向于避免交叉验证,而是只使用一个单一的验证分割,因为交叉验证可能在计算上是昂贵的。人们倾向于使用50%到90%的训练数据和剩余的数据来验证。这取决于多个因素:例如,如果超参数的数量很大,您可能更喜欢使用更大的验证分割。如果验证集中的样例数量很小(也许只有几百个左右),那么使用交叉验证就更安全了。在实践中可以看到的典型折叠数是3折、5折或10折交叉验证。
常见的数据拆分。给出了训练和测试集。训练集被分割成折叠(例如,这里有5个折叠)。折叠1-4成为训练集。一个折叠(例如,在黄色中的折叠5)被表示为验证折叠,并且用于调谐超参数。交叉验证每一步都选择其中1个折叠作为验证集,其余4个作为训练集,如此迭代计算5次。这就是为5折交叉验证。在最后,一旦模型被训练并且所有最佳的超参数被确定,模型在测试数据(红色部分)上被评估一次。
最近邻分类器的利弊
有必要聊聊最近邻分类器的优点和缺点。显然,一个优点是它很容易理解和实现。此外,分类器不需要时间来训练,只需要记住训练数据即可(代码中置于对象变量中即可)。然而,测试的成本高,因为分类测试样例需要与每个训练样例进行比较。这是主次颠倒的,因为在实践中,相比训练效率而言,我们更加关心测试效率。事实上,我们后面开发的深度神经网络将这个权衡转移到另一个极端:训练非常昂贵,但是一旦训练完成,对新的测试样例进行分类是非常快速。这种模式在实践中更为可取。
另一方面,最近邻分类器的计算复杂度是一个活跃的研究领域,并且存在一些近似最近邻(ANN)算法和库,它们可以加速数据集(例如FLANN)中的最近邻查找。这些算法允许在检索过程中权衡最近邻检索的正确性及其空间/时间复杂度,并且通常依赖于预处理/索引阶段,其涉及建立KD树,或运行k-均值算法。
最近邻分类器在某些场景中不失为一个好的选择(特别是如果数据是低维的),但是它很少适合在实际的图像分类场景中使用。其中一个问题是图像是高维对象(即它们通常包含许多像素),并且在高维空间上的距离可以是非常反直觉的。下图说明了我们开发的基于像素的L2相似性与人类感知相似性差得很多:
基于像素的高维数据(特别是图像)的距离可能是非常不符合直观的。这4张图像是一样的,但是原始图像(左)和紧邻它的三个其他图像的基于L2的像素距离都很远。显然,像素距离不完全对应于感知或语义相似性。
总结
- 我们介绍了图像分类的问题,其中我们给出了一组图像,它们都被标记为一个类别。然后,我们被要求预测一组新的测试图像的类别,并测量预测的准确性。
- 我们介绍了一个简单的分类器:最近邻分类器。我们看到,有多个超参数(如k值,或用于计算实例的距离的不同方法)与该分类器相关,并且没有明显的选择方法。
- 我们发现设置这些超参数的正确方法是将训练数据分割成两个:一个训练集和一个伪测试集,我们称之为验证集。我们尝试不同的超参数值,并使用在验证集上获得最佳性能的值。
- 如果缺乏训练数据,我们讨论了交叉验证,在估计哪一个超参数工作最好时,这种方法能减少噪声。
- 一旦找到最佳的超参数,我们就使用它们,并使用实际测试集执行一次评估。
- 我们看到最近邻算法在CIOWE10数据集上可以获得大约40%的精度。它很容易实现,但需要我们存储整个训练集,并且在测试图像数据集上进行评估是昂贵的。
- 最后,我们看到,在原始像素值数据集上使用L1或L2距离是不合适的,因为这种距离与图像的背景和颜色分布的相关性比它们的语义内容相关性更强。
在接下来的课程中,我们将着手解决这些挑战,最终得出解决方案,给出90%的精度,允许我们在学习完成后完全丢弃训练集,并且它们将允许我们在不到毫秒的时间内评估测试图像。
KNN在实践中的应用
如果您希望在实践中应用KNN(希望不是在图像上,或者仅仅作为起点),则如下进行:
- 数据归一化
- 降维。如果您的数据非常高维,考虑使用维度缩减技术,如PCA(Wiki REF,CS229 REF,BLOG REF),甚至随机投影。
- 将训练数据随机分解成训练数据和验证数据。通常情况下,训练数据在70%到90%之间。这个设置取决于你拥有多少个超参数以及你期望它们有多大的影响力。如果有许多超参数来估计,则应该在有较大验证集的一侧多表现,以有效地估计它们。如果您关心验证数据的大小,最好将训练数据分割成折叠并进行交叉验证。如果你能负担得起计算预算,那么使用交叉验证总是安全的(折数越多越好,但越贵)。
- 选择不同的K(越多越好)、跨越不同的距离类型(L1和L2是很好的候选)来训练和评估KNN分类器
- 如果您的KNN分类器运行时间过长,考虑使用近似最近邻库(例如FLANN)来加速检索(精度会降低)。
- 留意给出最佳结果的超参数。是否应该使用完整训练集来取得最佳超参数也是一个问题,因为如果要将验证数据折叠到训练集中(因为数据的大小会更大),则最优超参数可能会改变。在实践中,在最终分类器中不使用验证数据是更干净的,并且认为它在估计超参数时被烧毁。评估测试集上的最佳模型。报告测试集的准确性,并将结果声明为KNN分类器在数据上的性能。
斯坦福大学计算机视图课程,青星人工智能研究中心 翻译整理
1、数据驱动的图像分类方法
2、最近邻分类器
3、k - 最近邻分类器及使用验证集取得超参数
4、线性分类: SVM, Softmax
5、优化方法:随机梯度下降法
6、反向传播
7、神经网络一: 建立网络架构
8、神经网络二:设置数据和损失
9、神经网络 三:学习与评价
10、神经网络案例学习
11、卷积神经网络:结构、卷积/汇集层
12、理解与可视化卷积神经网络
13、传承学习与卷积神经网络调谐
原文地址 CS231n Convolutional Neural Networks for Visual Recognition