c++并查集（详细总结）

老话重谈，先看定义

并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。常常在使用中以森林来表示。

首先得明白一些概念：
什么是树，什么是森林（由树组成的叫森林hh），什么是集合
这些问题是其他范畴的知识，就不过多累赘了，不了解的同学建议提前了解先。

下面我们切入重点

1、并查集

首先，我个人认为并查集在逻辑上是一个森林，该森林内由一棵或多棵数组成，如下举个例子

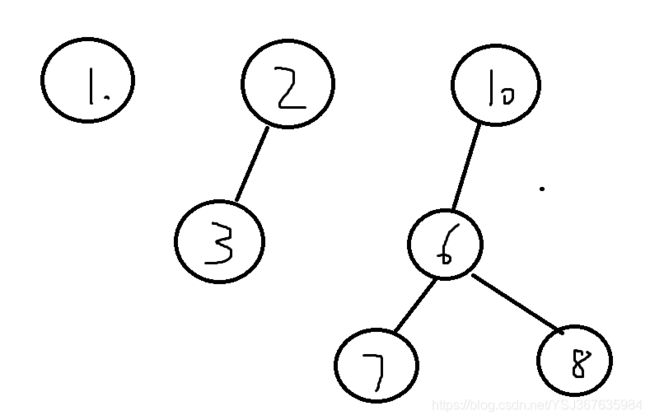
这三棵树可以组成一个森林，而这个森林可以叫并查集，每棵树可以称为并查集分量，这是逻辑上的理解

显式上理解，大部分情况并查集是以数组的方式进行存储的

有一些如下性质

• 每一个并查集分量（也就是每一棵树）都有一个根结点，比如上面三棵树的根结点分别是1，2，10
• 所属同一个并查集分量的结点的根结点是相同的，比如6，7，8的根结点都是10，所以这三个结点位于同一个并查集分量内，也就是同一颗树上
• 并查集每一个分量都是相互独立，互不影响的！
• 并查集内所有节点的值一定是互不相同的

2、常用并查集方法

在讲方法之前我们需要定义一些并查集需要用到的数据

数据存储	作用及举例
parent[]	parent[ i ] = j 表示 节点 i 的父节点是 j（比如上面根结点为10的那棵树，有 parent[ 7 ] = 6 , parent[ 6 ] = 10 …）
count	是一个int类型的变量，表示该并查集内有多少个并查集分量，也就是说并查集这个森林里面有多少课树（比如上面的例子中有三个树，所以count=3）

我们先定义并查集的数据结构代码（这里采用c++）

class DisjointSets{
    public:
         // 给个默认值，默认是10
        int count = 10;
        // vector的好处是可以动态修复数组大小
        vector<int> parent;
        // 类的有参构造方法
        DisjointSets(int count){
            this->count = count;
            // 对parent数组进行初始化
            for(int i=0;i<=count;++i)
                // 默认这个森林有count棵树，
                //而且每棵树只有一个节点，也就是
                // 根结点，默认根结点的父节点是根结点本身
                parent[i] = i;
        }
        // 类的析构函数，销毁类实例前调用
        ~DisjointSets(){}
        
        // 并查集的方法定义-----------------
        // 查找一个节点所属树的根节点
        int findParentNode(int x);
        // 合并两棵树
        void unionSetNode(int x,int y);        
};

2.1、并查集——查找某个节点的根结点

int DisjointSets::findParentNode(int x){
    // 如果x的父节点还是x，说明x就是根节点
    if(x == this->parent[x]) return x;
    // 否则继续找
    return findParentNode(this->parent[x]);
}

2.2、并查集——合并两个并查集分量(合并两棵树)

有些时候我们需要将一些并查集分量进行合并，以满足需求

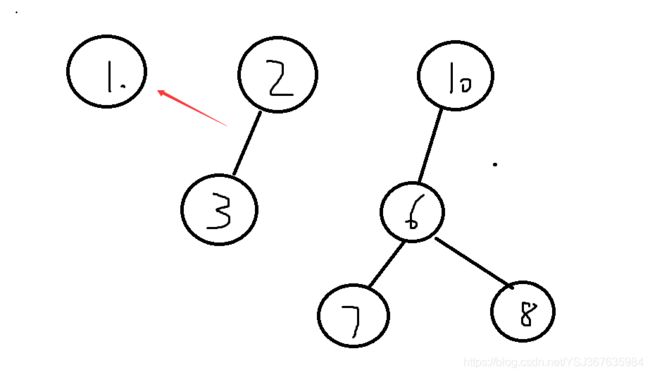
将根节点为 2 的树 合并到 根节点 为 1 的树上。
合并完成后 ，根节点 2 的父节点 不再是 2 了，而是 1，如下

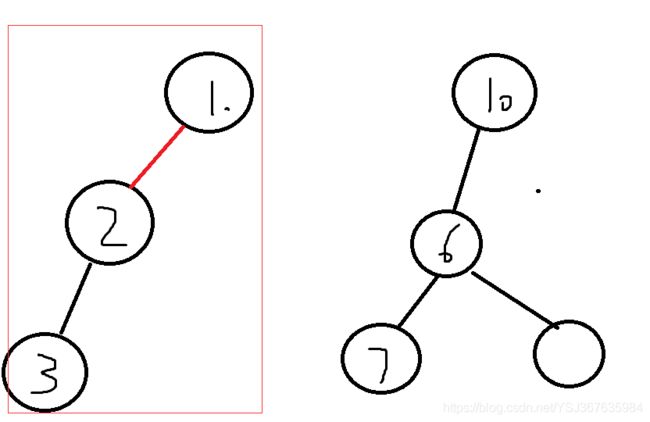
再合并之前我们还需要判断一些 需要合并的两个节点是否是同一个并查集分量（同一棵树上）
代码如下：

void DisjointSets::unionSetNode(int x,int y){
    // 先分别获取到 x 节点和 y节点 所属树的根节点
    int root_x = this->findParentNode(x);
    int root_y = this->findParentNode(y);
    // 如果两个节点的根节点相等，就不需要合并，是同一颗树的节点
    if(root_x == root_y) return;
    // 如果不相等,由于是y所属树合并到 x所属树上
    // 所以让 y所属树的根节点的父节点赋值为x所属树的根节点
    this->parent[root_y] = root_x;
    // 同时, 此时森林少了一颗树
    --this->count;
}

2.3、并查集查找根节点优化——路径压缩算法

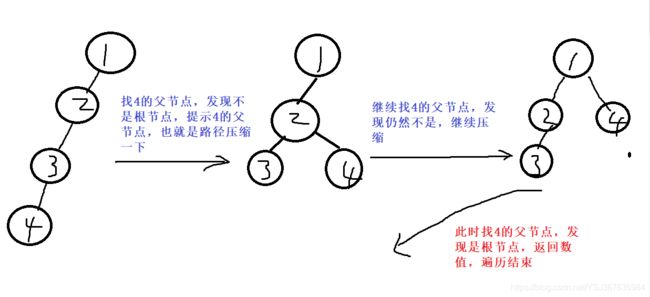
那么什么叫路径压缩内，我们先看看传统寻找某个节点所属树的根节点方法

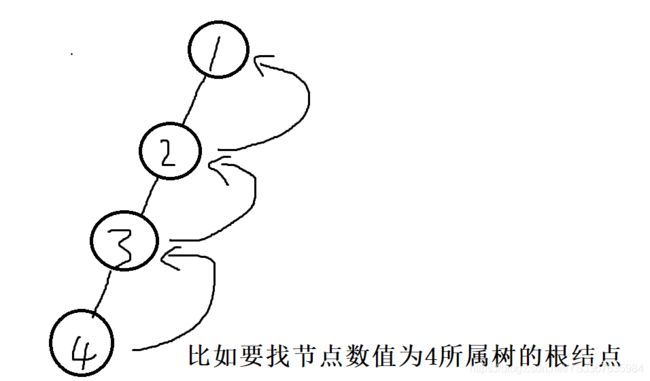
相当于，我们 4 所属树根结点，要遍历所可走路径。
如果我们只做一次还好，但是如果我们要重复寻找 4 的根节点，那是不是每次都要重复走一次，显得很浪费时间，所以，我们找到了一次 4 的根节点信息，直接用类似于备忘录的思想，把 4的父节点由3直接提升为1，这样子下次找就不用老是重复遍历了

代码如下：

int DisjointSets::findParentNode(int x){
    // 路径压缩改良版的查找
    // 如果 x的父节点是本身，说明x是根节点，退出循环，返回x
    while( x != this->parent[x] ){
        // 将 x 的父节点赋值为 x的父节点的父节点
        this->parent[x] = this->parent[this->parent[x]];
        // 改变此时x的值为 x的父节点
        x = this->parent[x];
    }
    return x;
}

下面可以来两道leetcode的题目练练手
547. 省份数量
839. 相似字符串组

两道题的代码答案分别是：

class Solution {
public:
    const static int N = 205;
    int parent[N];
    int count = 0;

    // 查找 x 的根结点
    int find(int x){
        return x==parent[x]?x:find(parent[x]);
    }
    // 合并,把 y 合并到 x内
    void megre(int x,int y){
        int root1 = find(x);
        int root2 = find(y);
        // 判断 x与y 是否位于同一个并查集分量内，是就返回，不需要合并
        if(root1 == root2) return;
        // y的根结点的父亲更新为x的根结点
        parent[root2] = root1;
        // 合并成功说明少了一个点
        --count;
    }
    // 初始化并查集数据
    void init(int n){
        // 所有点的根结点初始默认是本身
        for(int i=0;i<n;++i)
            parent[i]=i;
        // 初始count大小就是n
        count = n;
    }

    // 并查集的 第一题 实战
    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();
        // 初始化并查集
        init(n);
        for(int i = 0;i<n;++i){
            for(int j=0;j<n;++j){
                if(isConnected[i][j]==1){
                    megre(i,j);
                }
            }
        }
        return count;
    }
};

class Solution {
public:
    const static int N = 301;
    int parent[N];
    int count=0;
    /// 路径压缩
    int find(int x){
        while(x != parent[x]){
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    void union_set(int x,int y){
        int r1 = find(x);
        int r2 = find(y);
        if(r1==r2) return;
        parent[r2]=r1;
        --count;
    }
    void init(int n){
        count = n;
        for(int i=0;i<n;++i)
            parent[i]=i;
    }
    bool judge(string &s1,string &s2){
        int k = 0;
        for(int i=0;i<s1.size();++i)
            if(s1[i]!=s2[i])
                ++k;
        if(k<=2) return true;
        else return false;
    }
    // 考查并查集
    int numSimilarGroups(vector<string>& strs) {
        int n = strs.size();
        init(n);
        for(int i=0;i<n;++i)
            for(int j=i+1;j<n;++j)
                if(judge(strs[i],strs[j]))
                    union_set(i,j);
        return count;
    }
};