深度学习01 基本概念简介 李宏毅2022

2021 - (下) - 深度学习基本概念简介_哔哩哔哩_bilibili

this course focus on deep learning，函式是 类神经网路

 supervised learning

self- supervised learning，   pre-train（模型先练基本功

 downstream tasks下游任务

这个可以理解为，训练了编码器，也可以叫特征提取器

 

GPT-3  >  T5 > GPT-2 > BERT > ELMo

 GAN 生成对抗网络

刚开始时，18年，错误率比正确率高

最新的Facebook ，甚至某些时候unsupervised 比监督 效果还要好

不知道怎么标注资料，但可以定义成功时，reinforcement learning

进阶课题，不只是追求正确率。。。

异常检测 是说 让机器具备回答“我不知道”的能力

explainable AI 有很多变形，   这里 给机器一张图片，告诉我们，他觉得这张图里哪些地方重要

 注意，“机器比人厉害”骗局

 

 

 

 想要做一个“天网”到底有什么样的挑战，why没法让机器不断学习新技术

学习如何学习

meta learning= learn to learn

 让机器从大量任务里，自己发明新的演算法

---

套件 = 第三方库

 

Public分数是validation集上的结果，private分数是test集上的结果

验证数据集（validation dataset）是模型训练过程中留出的样本集，它可以用于调整模型的超参数和评估模型的能力。

深度学习 每次跑出来的结果都会有点不一样

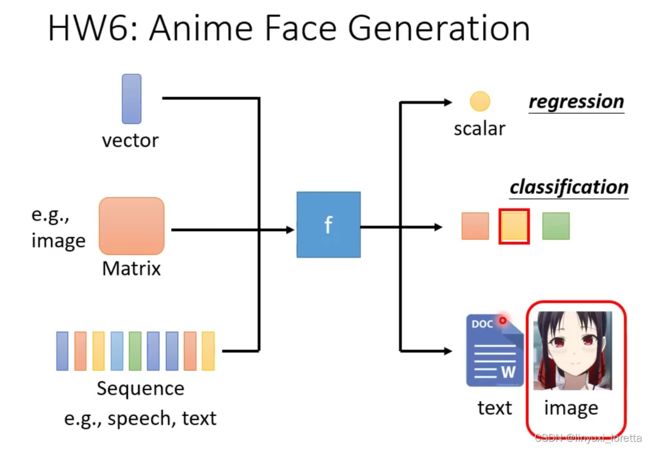
随着我们要找的函式不同，机器学习有不同的类别

 alpha go本身也是一個Classification

大家害怕碰触的问题，structured learning，机器产生一个有结构的物件，画图、写文章，

 三个机器学习的任务：regression、classification、structured learning

---

youtuber 他會在意頻道有沒有流量

我們有沒有可能找一個函式，输入是youtube後台的資訊、輸出是這個頻道   隔天的總點閱率總共有多少

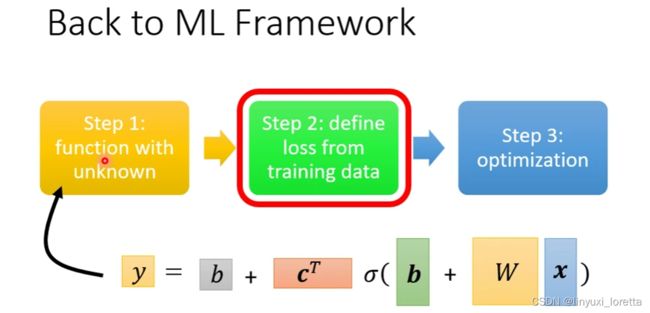
那機器學習找這個函式的過程、分成三個步驟、第一個步驟是我們要寫出一個  帶有未知參數的函式、簡單來說就是 我們先猜測一下、我們打算找的這個函式F、它的數學式到底長什麼樣子。

猜测来源于 对问题本质的了解，Domain knowledge

Model這個東西在機器學習裡面，就是一個帶有未知的Parameter的Function

step1，

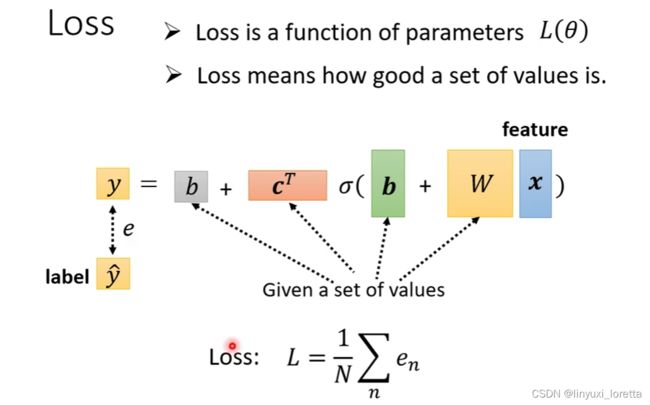
 step2，定義一個東西叫做Loss，Loss它也是一個Function，输入是Model裡面的參數，输出代表：如果我們把這一組未知的參數 設定某一個數值時，这组参数好是不好

計算y跟ŷ之間的差距、其實不只一種方式

mean absolute error（MAE）、mean square error（MSE）、。。。

MSE跟MAE其實有非常微妙的差別、通常你要選擇用哪一種方法來衡量距離、那是看你的需求和你對這個任務的理解

有一些任務如果y和ŷ它都是機率分布，你可能會選擇Cross-entropy交叉熵

 

你拿前一天的點閱的總次數，去預測隔天的點閱的總次數，可能前一天跟隔天的點閱的總次數其實是差不多的，所以w設1，然後b設一個小一點的數值，也許你的估測就會蠻精準的

 

step3，解一个最佳化的问题 ：找一個w跟b，可以讓我們的Loss func.最小，在這一門課裡面 我們唯一會用到的Optimization的方法  叫做Gradient Descent

首先你要隨機選取一個初始的點w₀.    那在往後的課程裡面，們其實會看到也許有一些方法，可以給我們一個比較好的w₀的值

那這一個算微分這件事啊 就是左右環視，看哪邊比較低  就往比較低的地方跨出一步

那這一步要跨多大呢，取决于两件事：斜率大這個步伐就跨大一點；η（ learning rate），那這種你在做機器學習需要自己設定的東西，叫做hyperparameters

不断重复，什麼時候會停下來呢，兩種狀況：第一種狀況是你失去耐心了，maybe我的上限就是設定100萬次，（更新幾次 也是一個hyperparameter）；另外一種理想上的停下來的可能是，當我們不斷調整參數，調整到一個地方  微分的值算出來正好是0的時候

Gradient Descent會有local minima的問題。教科書常常這樣講，但這個其實只是幻覺而已，假設你有做過深度學習相關的事情，有自己做過Gradient Descent 經驗的話，真正面對的難題不是local minima。

（因为维度太多，所以基本都是鞍点，真正的local minima基本遇不到）

pytorch裡面 算微分都是程式自動幫你算的

改进：

 

 發現：這藍色的線沒什麼神奇的地方，几乎就是 紅色的線往右平移一天而已

仔細觀察，這個真實的資料有一個很神奇的現象，周期性，這個真實的資料有一個很神奇的現象，那我發現那兩天都固定，是禮拜五跟禮拜六

通常一個模型的修改，往往來自於你對這個問題的理解，Domain Knowledge

所以一開始，我們對問題完全不理解的時候，我們就胡亂寫一個y=b+wx，並沒有做得特別好

接下來我們觀察了真實的數據以後，得到一個結論是，每隔七天有一個循環，所以我們應該要把，前七天的觀看人次都列入考慮

這邊考慮了比較多的資訊，在訓練資料上你應該要得到更低的loss

 

过拟合主要原因是选择的特征过多，导致无用特征或者相关性不大的特征也被参考了很大的权重

 這一種來自於 Model 的限制，叫 Model  Bias

紅色的這條曲線，可以看作是一個常數，再加上一群藍色的這樣子的 Function

Taylor展开的前提是n阶可导，这里不是Taylor就是分段而已，前面的别乱说

激活函数添加非线性因素，增强模型的表达能力

那也许我们今天要考虑的 x 跟 y 的关係不是 Piecewise Linear 的 Curves

 Taylor展开是用多项式的线性组合逼近原曲线

 每个蓝色的function 就是一个神经元

翻了数值分析的书，这叫分段线性拉格朗日插值

 

 （Sigmoid Function ） S 型的 Function

但不是只能用 Sigmoid 去逼近那個 Hard Sigmoid,完全有別的做法

 

所以我們其實有辦法寫出一個 ，非常有彈性的 ，有未知參數的 Function

 每一個 i 就代表了一個藍色的 Function，只是我們現在每一個藍色的 Function都用一個 Sigmoid Function 來比近似它，

 

 

 

 

 

 以上，我们重新改寫了機器學習的第一步，重新定了一個有未知參數的 Function

 

假設你有越多 Sigmoid,你就可以產生有越多段線的, Piecewise Linear 的 Function（分段线性函数）, 就可以逼近越複雜的 Function, 就可以逼近越複雜的 Function,這個又是另外一個 Hyper Parameter,

有了新的這個 Model 以後，未知的參數很多了，一個一個列出來很累，用 θ 來代表所有未知的參數

 L 前面放了一個倒三角形，Gradient 的簡寫，意思是：把所有的參數 θ1 θ2 θ3通通拿去對 L 作微分

那後面放 θ0 的意思是說，我們這個算微分的位置，是在 θ 等於 θ0 的地方

 

 

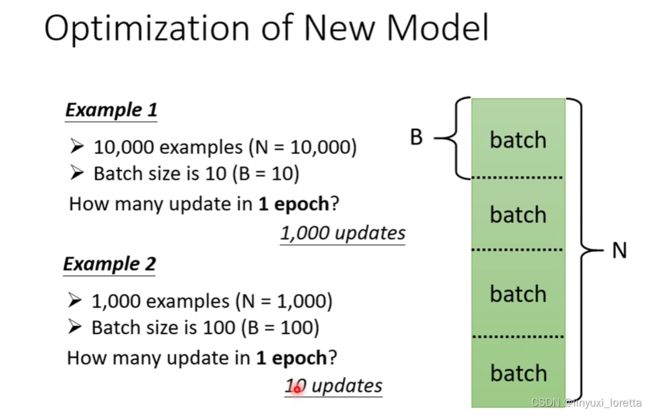
實際上我們在做 Gradient的時候，我們會把這大 N 筆資料分成一個一個的 Batch，随机分成一包一包。

假設這個 B 夠大，也許 L 跟 L1 會很接近 也說不定

每次我們會先選一個 Batch，用這個 Batch 來算 L，根據這個 L1 來算 Gradient，用這個 Gradient 來更新參數，接下來再選下一個 Batch 算出 L2，根據 L2 算出 Gradient，然後再更新參數

每次更新一次參數叫做一次 Update，把所有的 Batch 都看過一遍 叫做一個 Epoch

 Batch Size 的大小也是你自己決定的，（HyperParameter）

模型可以做更多变形：

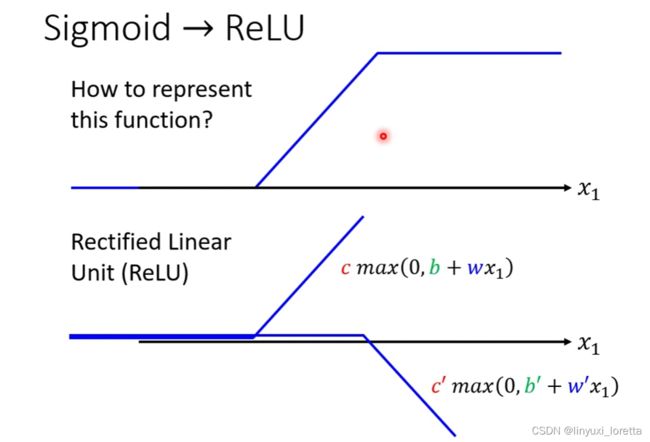
 Hard Sigmoid ，它可以看作是兩個 Rectified Linear Unit 的加總（ReLU）

 

 

 

 Sigmoid 跟 ReLU 應該是今天最常見的 Activation Function

我接下來的實驗都選擇用了 ReLU，顯然 ReLU 比較好，why

 

所以说从理论上讲两层的神经网络能够拟合任意函数，前提是神经元数目足够多

 100 個 ReLU 我們就可以產生 有 100 個折線的Piecewise Linear Function

1000 個 ReLU在訓練資料上 Loss 更低了一些，但是在沒看過的資料上看起來也沒有太大的進步

接下來還可以做什麼呢，還可以繼續改我們的模型

舉例來說，剛才我們說從 x 到 a 做的事情是什麼，是把 x *w + b，再通過 Sigmoid Function，不過我們現在已經知道說  通過 ReLU 也可以。得到a

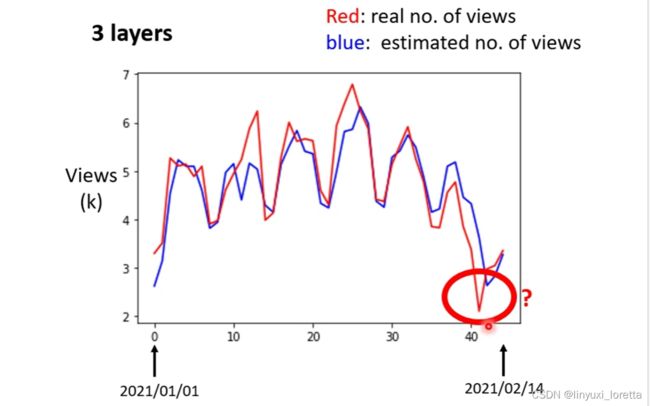
我們可以把這個同樣的事情，再反覆地多做幾次，那要做幾次，Hyper Parameter

某种程度上来说，越多的神经元层数能读取到的数据 特征就越多（相对而言）

有点像高数的逼近问题中多次调用同一个函数，一个已知点的横坐标通过一个函数得到一个函数值，然后又用这个函数值作为一个点的横坐标通过这个函数得到新的函数值，做越多次，函数值越精确，趋于无穷得到精确值

相当于一层画出了几段大折线，然后中间层画出大折线中的小折线

神经网络深度增加导致了可解释性很差，就是你也不知道为什么但就是结果很好

起初这个是实验出来的，不是理论假设后的验证

 

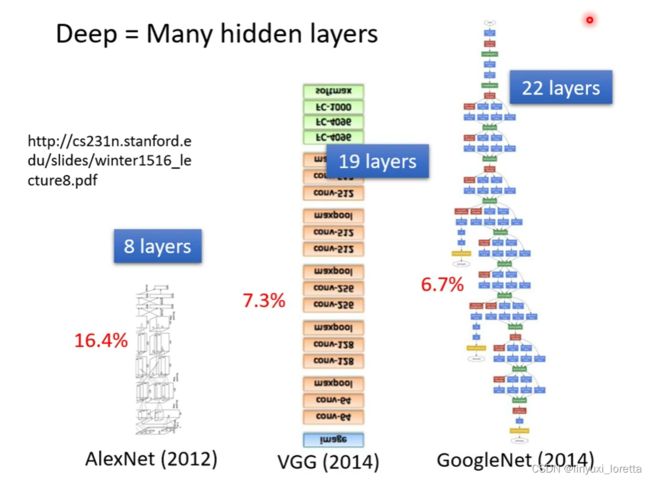
潮名字NN。80，90年代，后来臭掉了。       为了重振NN雄风， 改名叫 深度学习

后来越叠越多。。

 

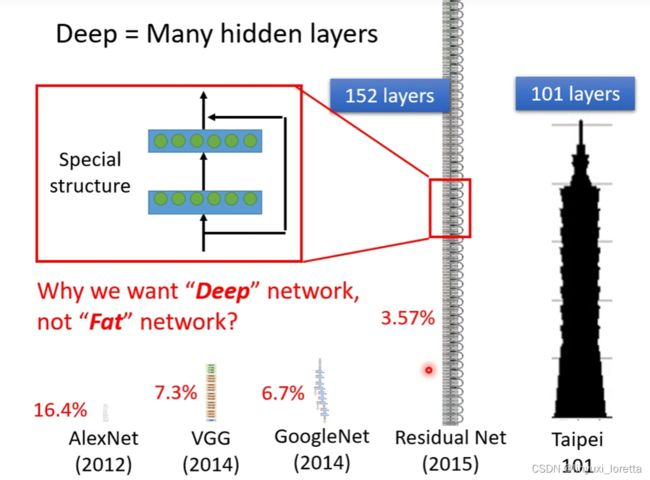 Residual Net   152层，要訓練這麼深的 Network 是有訣竅的

 

我們一開始說想要用 ReLU 或者是 Sigmoid去逼近一個複雜的 Function，實際上只要夠多的 ReLU 夠多的 Sigmoid，就可以知道夠複雜的線段，就可以逼近任何的 連續的 Function 。所以我們只要一排 ReLU 一排 Sigmoid  夠多就足夠了

為什麼我們不把 Network 變胖，只把 Network 變深呢

（一是，变胖的话会影响速度，模块化是最好的，二是，深度的神经网络可以自己学习参数重要性，自己调整参数权值）

深度學習的訓練，會用到一個東西叫 （Backpropagation）反向传播，其實它就是比較有效率算 Gradients 的方法，跟我們今天講的東西沒有什麼不同