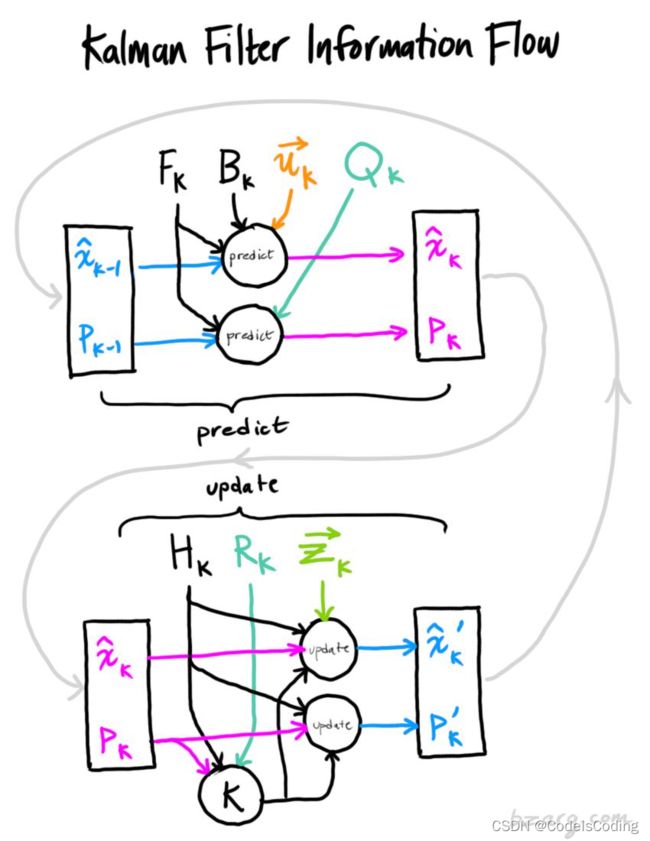
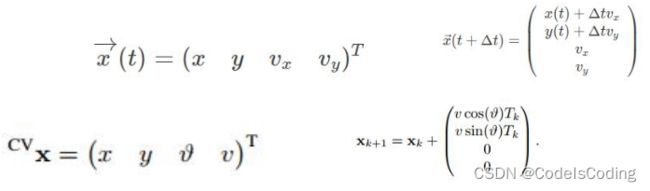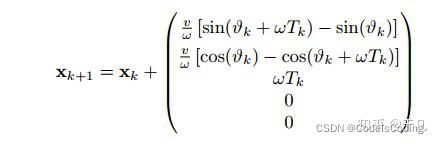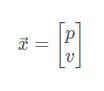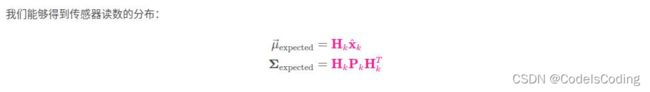卡尔曼滤波器之经典卡尔曼滤波
参考文献:
【1】http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
【2】https://blog.csdn.net/u010720661/article/details/63253509
【3】A geometric interpretation of the covariance matrix
【4】卡尔曼滤波器从理论到实践视频讲解-超详细
目录
1.卡尔曼滤波器简介
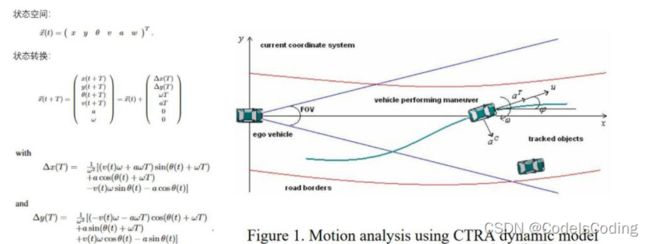
2.运动模型
3.经典卡尔曼滤波
3.1 最简单的数据融合——均值估计
3.2 经典卡尔曼滤波器数据融合
【1】How a Kalman filter sees your problem ?
【2】Describing the problem with matrices
【3】Refining the estimate with measurements
【4】 Putting it all together、
1.卡尔曼滤波器简介
卡尔曼滤波是指在含有噪声等不确定性信息的连续变化的动态系统中,对系统的状态进行预测和修正。简单来讲,卡尔曼滤波器就是根据上一时刻的状态,预测当前时刻的状态,将预测的状态与当前时刻的测量值进行加权,加权后的结果才认为是当前的实际状态,而不是仅仅听信当前的测量值。
这里的不确定性体现在:
1)不存在能够对某一系统进行完美建模的数学模型
2)系统受到的的扰动和干扰不可控,也难以数学建模
3 )任何的测量传感器都存在误差
卡尔曼滤波器只需要存储前一个状态的参数,不需要额外保留其他历史数据,因此具有内存占用小,计算速度快的优点,因此很适合应用于解决实时问题和嵌入式系统。如在自动驾驶领域,汽车行进过程中,我们会获得某一时刻,自车坐标系下的各种传感器数据,这些数据包括:
1 )障碍物的位置、速度、姿态(LiDar、Radar、视觉);
2 )车道线的视觉感知结果及曲线方程、类型和长度;
3 )自车的 GPS 坐标等等。
这些信号的组合,表示了无人车当前时刻的环境信息。由于传感器本身的特性,任何测量结果都是有误差的。以障碍物检测为例,如果直接使用传感器的测量结果,在车辆颠簸或其他外界条件影响时,可能会造成障碍物测量结果的突变,这对无人车的感知来说是不可接受的。因此需要在传感器测量结果的基础上,进行跟踪,以此来保证障碍物的位置、速度等信息不会发生突变。在无人车领域,卡尔曼滤波器除了应用于障碍物跟踪外,也在车道线跟踪、障碍物预测以及定位等领域大展身手。
2.运动模型
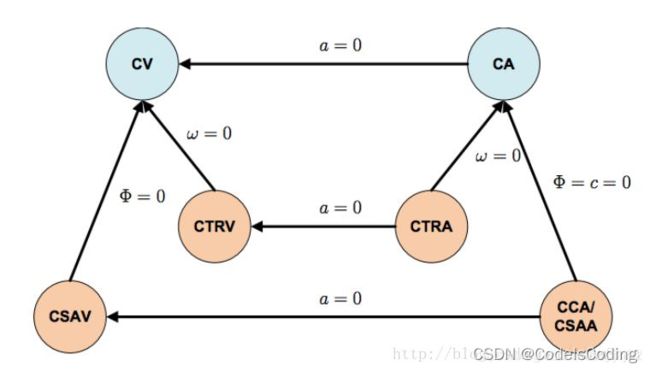
一次运动模型:这些线性运动模型假定目标是直线运动的,并不考虑物体的转弯。
● 恒定速度模型(Constant Velocity, CV)
● 恒定加速度模型(Constant Acceleration, CA)
二次运动模型:通常带有角速度,即车辆在做弧线运动
● 恒定转率和速度模型(Constant Turn Rate and Velocity,CTRV):以固定的转弯速率和恒定的速度大小移动,即匀速圆周运动
● 恒定转率和加速度模型(Constant Turn Rate and Acceleration,CTRA)
同 CTRV 相比,转速不变,说明在相同时间内转过的角度是一样的,径向由匀速变成匀加速。CTRA 多用于机载追踪系统,这些二次运动模型大多假定速度 v 和偏航角速度 ω没有关系。因此,在这类运动模型中,由于偏航角速度 ω 测量的扰动,即使车辆没有移动,运动模型下的角速度也会发生非常细微的变化。
为了解决这个问题,速度 v 和 偏航角速度 ω 的关联可以通过设定转向角Φ恒定来建立,也就是在汽车上通过方向盘控制轮胎转角,这样就引出了恒定转向角和速度模型(Constant Steering Angle and Velocity,CSAV),另外,速度可以被假定为线性变化的,进而引出了常曲率和加速度模型(ConstantCurvature and Acceleration,CCA)。
3.经典卡尔曼滤波
3.1 最简单的数据融合——均值估计
3.2 经典卡尔曼滤波器数据融合
 利用所有可用的信息,去得到一个更好的估计结果,这就是卡尔曼滤波的精髓。
利用所有可用的信息,去得到一个更好的估计结果,这就是卡尔曼滤波的精髓。
【1】How a Kalman filter sees your problem ?
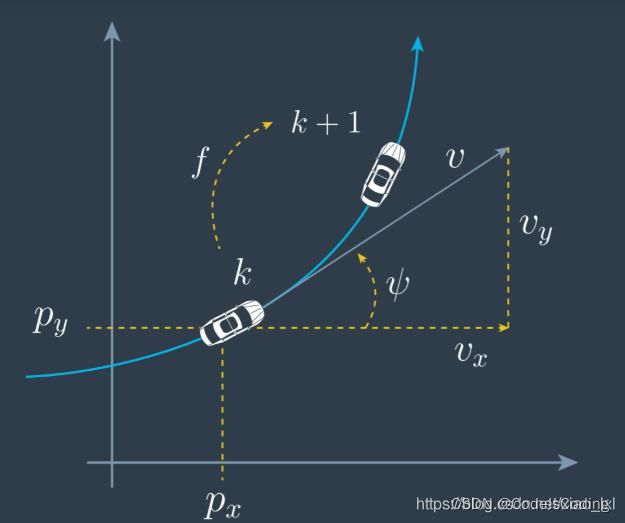
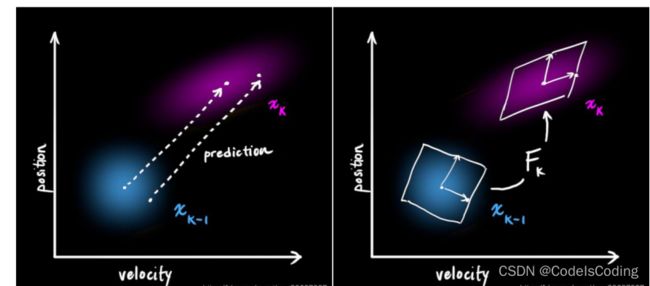
我们使用简单的状态,假设只有位置和速度的情况:
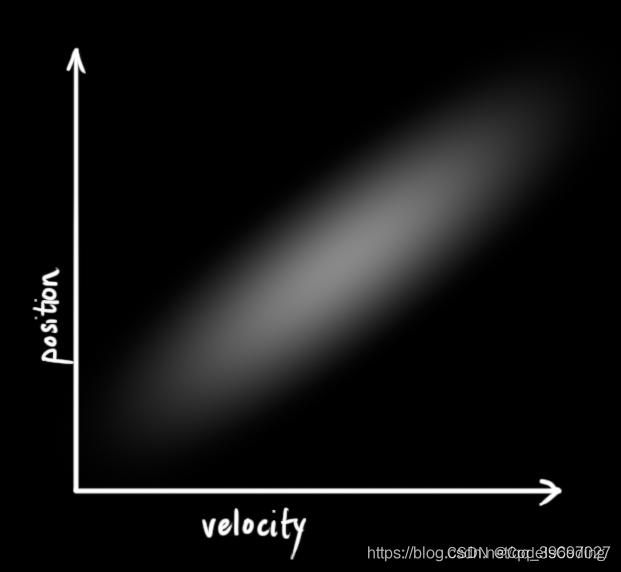
我们不知道实际的位置和速度,有一系列可能的位置与速度的组合,但是其中的一些可能性更高:
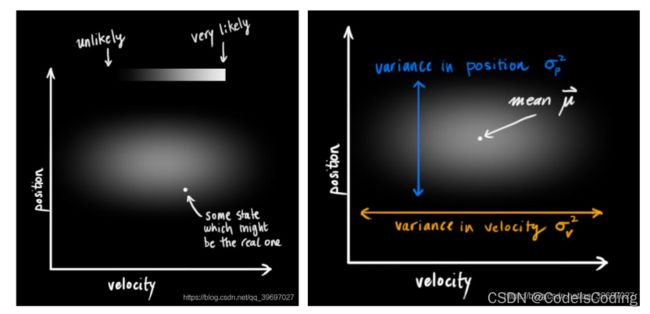 上图是一个二维高斯分布的投影图片,卡尔曼滤波假设两个变量(位置和速度)是随机高斯分布的。每个变量都有均值 μ (随机分布的中心)和方差σ2(表示不确定性)。上图表示的是位置和速度是不相关的,相关性的概念在概率论里有讲。大概意思就是一个变量不会告诉你另一个变量的信息。
上图是一个二维高斯分布的投影图片,卡尔曼滤波假设两个变量(位置和速度)是随机高斯分布的。每个变量都有均值 μ (随机分布的中心)和方差σ2(表示不确定性)。上图表示的是位置和速度是不相关的,相关性的概念在概率论里有讲。大概意思就是一个变量不会告诉你另一个变量的信息。
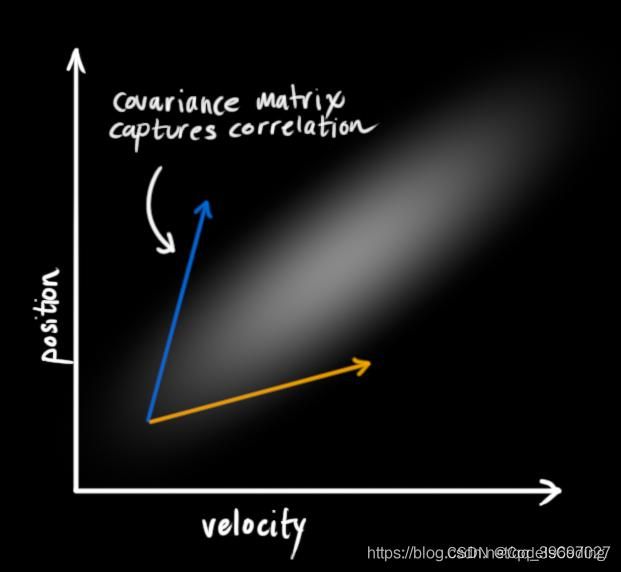
下面的例子更符合实际:位置和速度是相关的。一个指定位置的可能观测值取决于速度:
这种情况用于利用上一个旧的状态估计下一个状态,速度越大时物体运动的越远。这种关系在跟踪定位时非常重要,因为这会提供更多信息:一个测量值告诉我们其他测量值的可能范围。这就是卡尔曼滤波器的目标,我们希望从不确定的测量值中得到尽可能多的信息。
这种关系由协方差矩阵给出。简单来说,协方差矩阵的每个元素 Σij 都是第 i 个状态变量和第j 个状态变量的相关程度。(所以协方差矩阵是对称的,交换 i 和 j 并不影响),协方差矩阵通常用“ Σ”表示,所以将其元素称为“ Σij”。
【2】Describing the problem with matrices
用矩阵 Fk 表示该预测步骤:
●External influence
我们没有利用到所有信息,外部世界的某些变化可能跟状态没有关系,但是会影响到系统。例如列车员推动气阀会使车的速度变化,同样我们的机器人会发送指令给轮子走或停。如果我们知道更多的关于真实世界的信息,我们可以将这些写成一个向量叫做uk,加入到我们的预测作为一种修正。
例如我们知道加速度 a 表示控制指令,从基础的运动学公式:
●External uncertainty
如果这些状态量是基于系统自身的属性或者已知的外部控制作用来变化的,则不会出现什么问
题。 但是,如果存在未知的干扰呢?例如,假设我们跟踪一个四旋翼飞行器,它可能会受到风的干
扰,如果我们跟踪一个轮式机器人,轮子可能会打滑,或者路面上的小坡会让它减速。这样的话我们
就不能继续对这些状态进行跟踪,如果没有把这些外部干扰考虑在内,我们的预测就会出现偏差。
在每次预测之后,我们可以添加一些新的不确定性来建立这种与“外界”(即我们没有跟踪的干
扰)之间的不确定性模型:
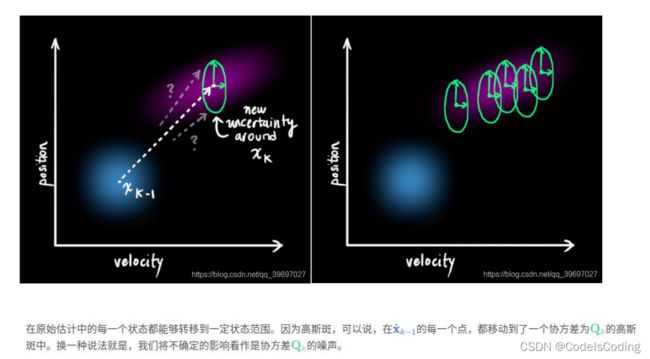 注:增加不确定性以前,原来的一个点转移到下一时刻就是根据方程算出来对应的某处,但是增
注:增加不确定性以前,原来的一个点转移到下一时刻就是根据方程算出来对应的某处,但是增
加了不确定性以后,可能在新的区域绿色框框内的某处了,这会产生一个新的高斯斑,有新的协方差
(相同的期望): 
以上可知:
 【3】Refining the estimate with measurements
【3】Refining the estimate with measurements
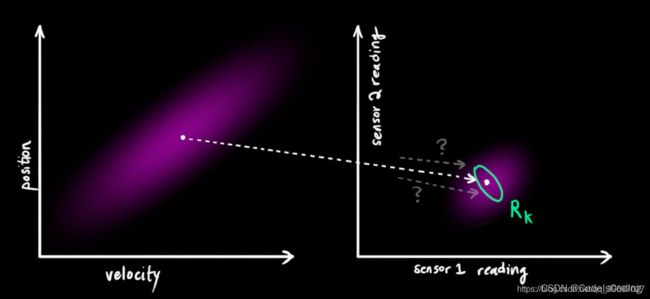
系统有一些传感器,间接给一些状态信息,换句话说就是:传感器在某一状态,给出一系列读数。如激光雷达测量的位置信号为笛卡尔坐标系下的 x 方向和 y 方向上的距离,毫米波雷达测量的是极坐标下的位置和角度信息。
传感器的测量单位和量程可能与系统状态的不同,此时我们需要用矩阵 H k 进行尺度转换,这个 H k 被称为测量矩阵(Measurement Matrix)。
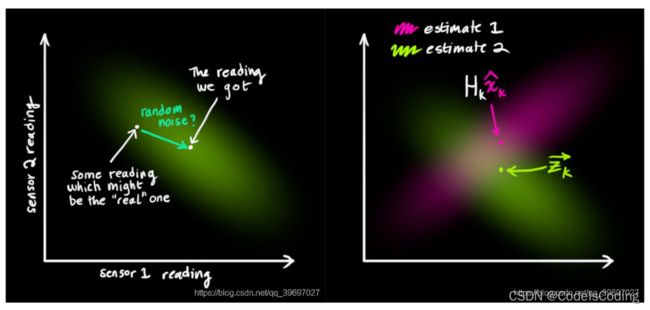
卡尔曼滤波适合于处理传感器的噪声。也就是说,传感器多少都会有些不可靠性,原始估计中的每一个状态的传感器读数都会是一个范围值。从我们观测到的每一个读数,我们可能猜测系统在一个特定的状态。但是因为存在不确定性,观测到的数据中某些状态的可能性会比较高。(眼见不一定为实,某些数据偏高了)
称这个不确定性(传感器噪声)的协方差为 R k , 该分布的期望和观测到的读数相同,称为 z k 。现在,我们得到两个高斯斑:一个表示系统状态预测;一个表示传感器测量。
接下来就是要协调预测值和传感器测量值。所以哪个更接近真实的状态呢?如果我们有两个概率分布,并且想知道两者都为真的概率(重叠),只需要把他们相乘(概率论)。重叠的部分就是最有可能的部分,就是根据已有的新的的最好估计。看起来像另一个高斯斑(gaussian blob)。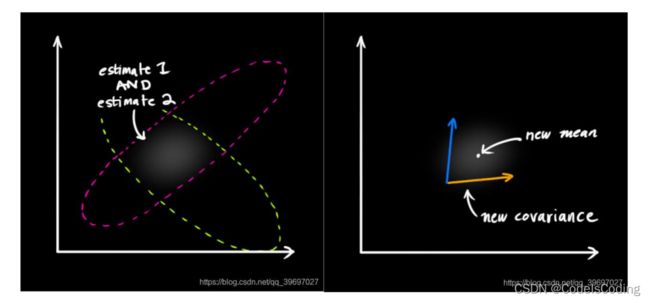
需要知道的是两个一维高斯分布的乘积是一个新的高斯分布,公式如下:
详细推导过程可以参考(视频): kalman 增益超详细推导
【4】 Putting it all together、
卡尔曼滤波器可以对任何线性系统进行精确建模。对于非线性系统,可以使用扩展卡尔曼滤波,
就是对期望值的预测和测量线性化,请见《卡尔曼滤波器之扩展卡尔曼滤波》。