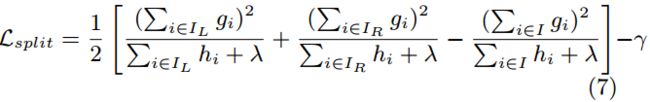XGBoost论文解读

本博客分为三块——正则化的目标函数、切分点查找算法和高效实现，分别对XGBoost原论文的第2、3和4章进行了探讨。

正则化的目标函数：

        XGBoost也是一种提升方法。相较于GBDT来说，它们的预测函数都是如下式(1)的加性函数（additive function），可以看到，预测函数对某一输入 X_i 输出就是输入实例在K颗树中输出的累和；它们的不同之一是目标函数的不同。

                                               

GBDT通过经验函数最小化来确定预测函数的参数，XGBoost在经验函数的基础上加上正则化项，其中表示单棵树的正则化，正则化项表征了模型的复杂度，通过选择合适的参数限制模型复杂度，能够避免过拟合。

                                                     

XGBoost中单棵树的正则化项由两项组成，分别是叶子结点的数量T和叶子权重矩阵w——叶子输出，的L2范数。当=0，剩下的项就是GBDT的目标优化函数。

       GBDT通过梯度下降法优化目标函数，梯度下降法是一种启发式优化算法，有可能陷入局部最优解。它们的不同之二是XGBoost优化的是经泰勒展开后近似的目标函数，该损失函数的推导如下，设： 

                                                                                 

表示第i个实例在第t次迭代上的输出，第t次迭代的结果是产生第t颗树（boosting tree）。那么对第t颗树来说，其需要优化的目标函数将是如下：

                                                       

对上式进行二阶泰勒展开得到如下的近似目标函数：

                                      

其中，

 ，    分别是损失函数在当前模型的一阶和二阶偏导（gradient statistics）。当前模型已知，也就是当前模型对训练数据的误差已知，为常量，对目标函数的优化没有影响，移除得到如下的目标函数：

                                             

对于二次函数来说，我们可以求出解析解，这也是泰勒展开的目的。定义叶子结点j上的实例集合为，对(3)进一步处理、展开可以得到(4)式

                                   

在(4)式中，目标函数对叶子结点权重求导，令导数=0，可以得到目标函数的解析最优解

                                                         

将解析解带入(4)式可以得到目标函数最优值

                                             

到这里可能会有一个疑问：既然解析解都出来了，咋还上不了天呢？观察到最优解叶子结点j的权重w*_ j其实是跟树的结构有关，换句话说就是训练数据集中有多少以及哪些数据分到叶子结点j上面有关，所以论文的后续大部分在讨论怎么确定树结构。论文是用(6)式作为scoring function来衡量树的好坏。树的生成主要是对于选定的feature怎么选择切分点，由于CART回归树采用二分法进行树生成，也就是对于选定的feature只选择一个切分点将数据分到切分点的两边，所以论文采用(7)式衡量切分点的增益。

                            

另外论文还采用了Shrinkage和Column Subsampling来防止过拟合。

切分点查找算法

        exact greedy algorithm是一种切分点查找算法，如Algorithm 1所示。该算法对于每一个feature，试图枚举出所有可能的切分点，并计算在每一个切分点上的增益，从而选择增益最好的切分点。在algorithm1中要枚举出所有的可能的切分点，算法是首先对所有训练数据对feature k的取值进行排序，这样就能轻易地枚举出所有的切分点。

                                                            

        exact greedy algorithm很强大，但当训练数据量太大以至于无法完全读进内存或者运行在分布式计算资源上，就有问题了。所以论文总结了一种approximate algorithm, 如algorithm 2

                                                         

algorithm2针对feature k先是根据特征分布的percentile列出了L个待选切分点（candidate splitting point），切分点值的集合S_k，之后根据(7)式分别计算这些待选切分点的增益，选择增益最好的切分点。根据feature k大小不同——是在训练的一开始就对全部训练数据的feature k列出待选切分点还是对分到某个结点上的训练数据的feature k，approximate algorithm有两种变体——global、local.

        论文提出了加权分位数（weighted quantile）用于上述提到的待选切分点（percentile）的选择。具体来说，假设有数据集，表示实例1、2、...、n的特征k的值和其二阶偏导，则有如(8)所示的rank function，根据该rank function选择待选切分点。加权的意思rank function是用二阶偏导计算，也就是给每个实例以权重，该权重是实例点的二阶偏导。(8)式rank function表示对于特征k，小于z的实例占总数的比重，这里的总数根据global还是local而定。

                                                         

根据需要选择的待选切分点数量，我们可以得到分位数S_k.

                                            

在实际场景中，数据缺失很常见，如果某实例点的特征值缺失，上述算法无法将该实例点分到任一子结点。对此论文提出了稀疏感知的切分点查找算法。原理大概是对于特征值缺失的实例点，分别将其分到左右子结点，计算增益，选择增益最好的划分方式作为该特征缺失情况下的默认划分。

                                                                  

高效实现

       论文提出了一种内存单元——block，训练数据以compressed sparse column(CSC)的方式存储在block中，block中每个column都根据特征值排好序的，排序后的column依然存有row_index的信息，根据row_index可以拿到对应的一阶和二阶偏导。 

        对于exact greedy algorithm（algorithm 1），需要将所有训练数据存到同一个block中，这样在算法过程中，数据不再需要重新排序。对于approximate algorithm（algorithm 2），可以使用多个block，每个block存储的是训练数据的子集，这些block可以是分布式的或者核外存储单元。更重要的是计算增益步骤，对于不同的特征k可以并行进行。

        这里可能会有两个问题，首先当使用多个block时，每个block只存储训练数据的子集，在累加gradient statistics（即计算(7)式表征的增益）时，由于block可能是分布式或其他情况，或者block太大与cache不匹配，没办法快速拿到；另外由特征值经row_index取gradient statistics是非连续访问，可能取值不在当前内存单元。这些都是造成cache miss.

       论文针对这些问题，提出了cache-aware访问方法。具体来说，针对exact greedy algorithm，对每个thread分配一个internal buffer，相当于一个高速缓存，然后以一种小批量累加的方式逐步计算增益，每次计算前，先将所需的gradient statistics拿到高速缓存中；对于approximate algorithm，我们通过选择合适的block大小来平衡并行效率和cache miss问题。

        CPU速度远高于外设读取速度，所以对于核外存储block，论文后面还使用了两种技术——block compression、block sharding来提高核外存储的计算能力。

 

本文所有公式、算法均截取自Tianqi Chen的论文——XGBoost: A Scable Tree Boosting System.