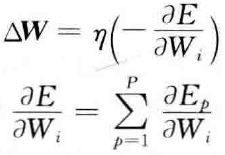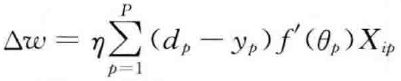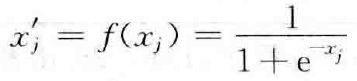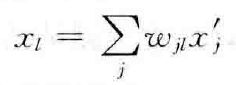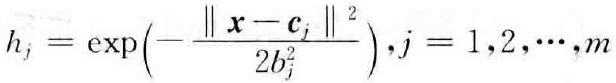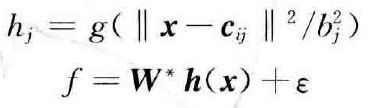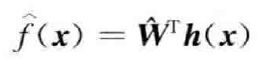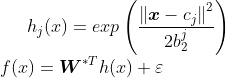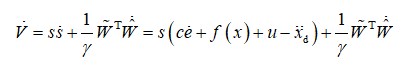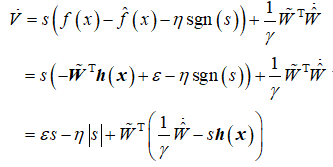强化学习6——神经网络基础知识

一、概念及性质

1.1 概念

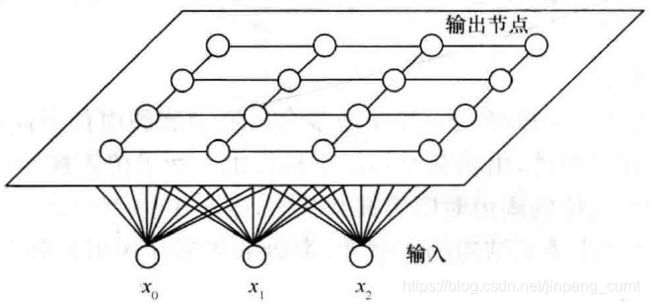
人工神经网络（简称神经网络，Neural Network）是模拟人脑思维方式的数学模型。神经网络控制是将神经网络与控制理论相结合而发展起来的智能控制方法。它已成为智能控制的一个新的分支，为解决复杂的非线性、不确定、不确知系统的控制问题开辟了新途径。典型神经网络有如下三种：

                       (a)前向网络                                                 (b)反馈网络                                          (c)自组织网络

                                                                                 图1 三种典型神经网络

1.2 特征

神经网络具有以下几个特征：

（1）能逼近任意非线性函数；

（2）信息的并行分布式处理与存储；

（3）可以多输入、多输出；

（4）便于用超大规模集成电路（VISI）或光学集成电路系统实现，或用现有的计算机技术实现；

（5）能进行学习，以适应环境的变化。

1.3 神经网络算法

目前神经网络的学习算法有多种，按有无导师分类，可分为有导师学习（Supervised Learning）、无导师学习（Unsupervised Learning）和再励学习（Reinforcement Learning）等几大类。

                                         

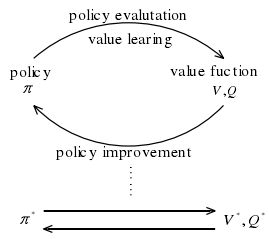
                                                                          图2 有导师指导的神经网络学习

在有导师的学习方式中，网络的输出和期望的输出（即导师信号）进行比较，然后根据两者之间的差异调整网络的权值，最终使差异变小，如图2所示。

                                                         

                                                                              图3 无导师指导的神经网络学习

在无导师的学习方式中，输入模式进入网络后，网络按照一种预先设定的规则（如竞争规则）自动调整权值，使网络最终具有模式分类等功能，如图3所示。

                                               

强化学习是介于上述两者之间的一种学习方式。

1.4  神经网络控制的研究领域

（1）基于神经网络的系统辨识

① 将神经网络作为被辨识系统的模型，可在已知常规模型结构的情况下，估计模型的参数。

②利用神经网络的线性、非线性特性，可建立线性、非线性系统的静态、动态、逆动态及预测模型，实现系统的建模和辨识。

（2）神经网络控制器

神经网络作为控制器，可对不确定、不确知系统及扰动进行有效的控制，使控制系统达到所要求的动态、静态特性。

（3）神经网络与其他算法相结合

将神经网络与专家系统、模糊逻辑、遗传算法等相结合，可设计新型智能控制系统。

（4）优化计算

在常规的控制系统中，常遇到求解约束优化问题，神经网络为这类问题的解决提供了有效的途径。

目前，神经网络控制已经在多种控制结构中得到应用，如PID控制、模型参考自适应控制、前馈反馈控制、内模控制、预测控制、模糊控制等。

二、基于梯度下降的权值调整策略

2.1  Delta学习规则

假设误差准则函数为

                                                                       

式中，代表期望的输出（导师信号）；为网络的实际输出，，为网络所有权值组成的向量，即

                                                                        

为输入模式，即

                                                        

式中，训练样本数为。

神经网络学习的目的是通过调整权值，使误差准则函数最小。可采用梯度下降法来实现权值的调整，其基本思想是沿着的负梯度方向不断修正值，直到E达到最小，这种方法的数学表达式为

                                                         

其中

                                                      

令网络输出为，则

                                                             

                         

W的修正规则为

                                                

上式称为Delta学习规则，又称误差修正规则。

Hebb学习规则和Delta学习规则都属于传统的权值调节方法，而一种更先进的方法是通过Lyapunov稳定性理论来获得权值调节律的。

三、BP神经网络

                                              

                                                              

                                                                             

3.1 特点

BP网络具有以下几个特点：

（1）BP网络是一种多层网络，包括输入层、隐层和输出层；

（2）层与层之间采用全互连方式，同一层神经元之间不连接；

（3）权值通过Delta学习算法进行调节；

（4）神经元激发函数为S函数；

（5）学习算法由正向传播和反向传播组成；

（6）层与层的连接是单向的，信息的传播是双向的。

 

四、RBF神经网络

4.1 基本概念

                                                      

                                            

 

                                           

RBF网络的学习过程与BP网络的学习过程类似，两者的主要区别在于各使用不同的作用函数。BP网络中隐层使用的是Sigmoid函数，其值在输入空间中无限大的范围内为非零值，因而是一种全局逼近的神经网络；而RBF网络中的作用函数是高斯基函数，其值在输入空间中有限范围内为非零值，因而RBF网络是局部逼近的神经网络。

 

4.2 基于RBF网络的函数逼近

RBF网络可对任意未知非线性函数进行任意精度的逼近。在控制系统设计中，采用RBF网络可实现对未知函数的逼近。

                               

例如，为了估计未知函数，可采用如下RBF网络算法进行逼近

                                                            

式中，为网络输入，表示输入层节点，为隐含层节点，为隐含层的输出，为理想权值，为网络的逼近误差，。

在控制系统设计中，可采样RBF网络对未知函数进行逼近。一般可采用系统状态作为网络的输入，网络输出为

                                                        

式中，为估计权值。

在实际的控制系统设计中，为了保证网络的输入值处于高斯基函数的有效范围，应根据网络的输入值实际范围确定高斯基函数中心点坐标向量值；为了保证高斯基函数的有效映射，需要将高斯基函数的宽度取适当的值。的调节是通过闭环的Lyapunov函数的稳定性分析中进行设计的。

 

五、仿真实例

5.1 问题描述

考虑如下简单非线性系统

                                                                                                (1)

其中未知。

位置指令为，则误差及其变化率为

                                                                              (2)

定义误差函数为

                                                                                         （3）

则

                                                

由（3）可知，如果，则 。         

5.2 控制设计

由于RBF的万能逼近特性，可采用RBF神经网络逼近：

                                                      

的近似值如下：  

                                                                     

其中，为高斯函数输出，为网络权值的估计值。

由于

                           

其中，。

定义李亚普洛夫函数

                                                            

则

                            

设计控制律为

                                                            

则

                                        

取，自适应率为

                                                      

则

                                                       

5.3 结果与分析

系统仿真图如下：

                 

1. 系统模型

function [sys,x0,str,ts]=s_function(t,x,u,flag)
switch flag,
%Initialization
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
case 1,
    sys=mdlDerivatives(t,x,u);
%Outputs
  case 3,
    sys=mdlOutputs(t,x,u);
%Unhandled flags
  case {2, 4, 9 }
    sys = [];
%Unexpected flags
  otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end
%mdlInitializeSizes
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 2;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 3;
sizes.NumInputs      = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[0.15;0];
str=[];
ts=[];
function sys=mdlDerivatives(t,x,u)
ut=u(1);

f=10*x(1)*x(2);
sys(1)=x(2);
sys(2)=f+ut;
function sys=mdlOutputs(t,x,u)
f=10*x(1)*x(2);

sys(1)=x(1);
sys(2)=x(2);
sys(3)=f;

2. 控制器

function [sys,x0,str,ts] = spacemodel(t,x,u,flag)
switch flag,
case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
case 1,
    sys=mdlDerivatives(t,x,u);
case 3,
    sys=mdlOutputs(t,x,u);
case {2,4,9}
    sys=[];
otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
global b c lama
sizes = simsizes;
sizes.NumContStates  = 5;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 2;
sizes.NumInputs      = 4;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0  = 0.1*ones(1,5);
str = [];
ts  = [0 0];
c=0.5*[-2 -1 0 1 2;
       -2 -1 0 1 2];
b=3.0;
lama=10;
function sys=mdlDerivatives(t,x,u)
global b c lama
xd=sin(t);
dxd=cos(t);

x1=u(2);
x2=u(3);
e=x1-xd;
de=x2-dxd;
s=lama*e+de;

W=[x(1) x(2) x(3) x(4) x(5)]';
xi=[x1;x2];

h=zeros(5,1);
for j=1:1:5
    h(j)=exp(-norm(xi-c(:,j))^2/(2*b^2));
end

gama=1500;
for i=1:1:5
    sys(i)=gama*s*h(i);
end

function sys=mdlOutputs(t,x,u)
global b c lama
xd=sin(t);
dxd=cos(t);
ddxd=-sin(t);

x1=u(2);
x2=u(3);
e=x1-xd;
de=x2-dxd;
s=lama*e+de;

W=[x(1) x(2) x(3) x(4) x(5)];
xi=[x1;x2];

h=zeros(5,1);c
for j=1:1:5
    h(j)=exp(-norm(xi-c(:,j))^2/(2*b^2));
end
fn=W*h;
xite=1.50;

%fn=10*x1+x2;  %Precise f
ut=-lama*de+ddxd-fn-xite*sign(s);

sys(1)=ut;
sys(2)=fn;

 

3. 绘图

close all;

figure(1);
subplot(211);
plot(t,x(:,1),'r',t,x(:,2),'b');
xlabel('time(s)');ylabel('position tracking');
subplot(212);
plot(t,cos(t),'r',t,x(:,3),'b');
xlabel('time(s)');ylabel('speed tracking');

figure(2);
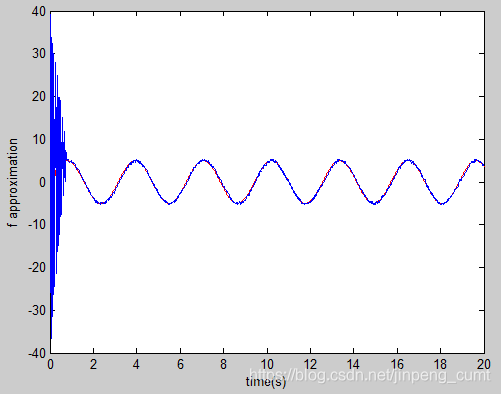
plot(t,f(:,1),'r',t,f(:,3),'b');
xlabel('time(s)');ylabel('f approximation');

仿真结果如下