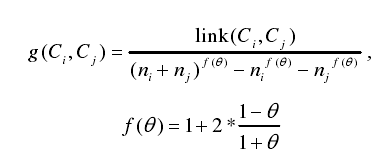层次聚类算法_层次方法概述
前 言
层次聚类算法对给定的数据进行层次分解,直到某种条件满足为止,具体有可分为凝聚的和分裂的两种方案。凝聚的层次聚类是一种自底向上的策略,首先将每个对象作为一个簇然后合并这些原子簇为越来越大的簇,直到多有的对象都在一个簇中或者到底某个条件终止;分裂的层次聚类与凝聚的层次聚类相反,采用的是自顶向下的策略,它首先将所有对象置于一个簇中然后逐渐细分为越来越小的簇,直到每个对象自成一簇,或者到某个终止条件.
层次聚类方法是通过将数据组织为若干组并形成一个相应的树来进行聚类的。根据层次分解是自底而上还是自顶而下形成的,层次聚类算法可以进一步分为凝聚方法(agglomerative method)和分裂方法(divisive method)两种。本章主要讨论了层次聚类方法,通过分析传统的层次聚类方法的不足之处,提出了一种基于动态近邻选择模型的Chameleon算法。一个纯粹的层次聚类方法的聚类质量受限于:一旦一个合并或分裂被执行,就不能修正。也就是说,如果某个合并或分裂决策在后来证明是不好的选择,该方法无法退回并更正。
层次方法概述
1 凝聚的和分裂层次聚类
一般来说,有两种类型的层次聚类方法:
(1)凝聚的层次聚类:这种自底向上的策略首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到所有的对象都在一个簇中,或者某个终结条件被满足。绝大多数层次聚类方法属于这一类,它们只是在簇间相似度的定义上有所不同。
(2)分裂的层次聚类:这种自顶向下的策略与凝聚的层次聚类相反,它首先将所有对象置于一个簇中,然后逐步细分为越来越小的簇,直到每个对象自成一簇,或者达到了某个终结条件,例如达到了某个希望的簇数目,或者两个最近的簇之间的距离超过了某个阈值。
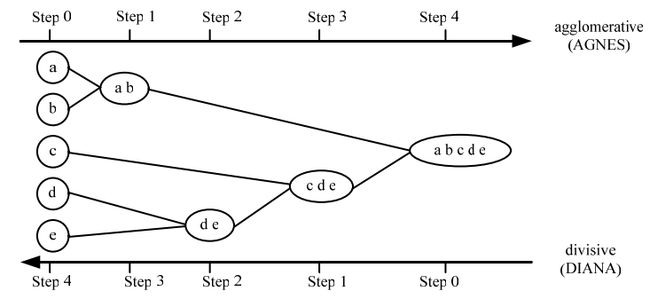
图 1 描述了凝聚的层次聚类方法 AGNES(Agglomerative Nestling)和分裂的层次聚类方法 DIANA(Divisive Analysis)在一个包含五个对象的数据集合{}a,b,c,d,e} 上的处理过程。其中,对象间距离函数采用欧式聚类,簇间距离采用最小距离。在 AGNES 中,选择簇间距离最小的两个簇进行合并。而在 DIANA 中,按最大欧式距离进行簇分裂。
层次聚类方法的优点在于可以在不同粒度水平上对数据进行探测,而且容易实现相似度量或距离度量。而层次聚类算法的困难在于合并或分裂点的选择。这样的决定是非常关键的,因为一旦一组对象被合并或者分裂,下一步的处理将在新生的簇上进行。己做的处理不能被撤销,聚类之间也不能交换对象。如果在某一步没有很好地选择合并或分裂的决定,可能会导致低质量的聚类结果。而且,这种聚类方法不具有很好的可伸缩性,因为合并或分裂的决定需要检查和估算大量的对象或簇。
图 1 凝聚和分裂层次聚类
2 簇间距离度量方法
对于任意两个簇之间的距离度量,有以下四种方法:
(1)最小距离(单链接方法):是指用两个聚类所有数据点的最近距离代表两个聚类的距离。
(2)最大距离(完全链接方法):是指用两个聚类所有数据点的最远距离代表两个聚类的距离。
(3)均值的距离(质心方法):是指用两个聚类各自中心点之间的距离代表两个聚类的距离。
(4)平均距离(平均链接方法):是指用两个聚类所有数据点间的距离的平均距离。
其中,簇间距离(相似度)的函数很多,最常用的度量准则是欧几里得距离。不同的距离函数可以得到不同的层次聚类方法。
3 主要的几种层次聚类方法
目前,比较有代表性的层次聚类算法有:BIRCH 算法、 CURE 算法、ROCK 算法和 Chameleon 算法。
3.1 BIRCH 算法
BIRCH(利用层次方法进行平衡迭代规约和聚类)算法是一个综合的层次聚类方法。它首先将数据集以一种紧凑的压缩格式存放,然后直接在压缩的数据集(而不是原始的数据集)上进行聚类,所以其 I/O 成本与数据集的大小呈线性关系。BIRCH 特别适合大数据集,且支持增量聚类或动态聚类。算法扫描数据集一遍就可生成较好的聚类,增加扫描次数可用来进一步改进聚类质量。它引入用于概括簇信息的两个概念:聚类特征(Clustering Feature)和聚类特征树(CF树)。一个聚类特征是一个三元组,给出对象子聚类信息的汇总描述。假设某个子
从统计学的观点来看,聚类特征是对给定子聚类的统计汇总:子聚类的 0 阶矩,1 阶矩,以及 2 阶矩。它记录了计算聚类和有效利用存储的关键度量,因为它汇总了关于子聚类的信息,而不是所存储的对象。一个 CF 树是高度平衡的树,它存储了层次聚类的聚类特征。
BIRCH 采用了一种多阶段聚类技术:数据集的单遍扫描产生了一个基本的聚类,一遍或多遍的额外扫描可以进一步改进聚类质量。这个算法的所需时间复杂度是O(n) 。n 是对象的数目。BIRCH 算法具有对对象数目的线性伸缩性,及较好的聚类质量。但是,CF 树的每个节点由于大小限制只能包含有限数目的条目,一个CF树节点并不总是对应于用户所认为的一个自然聚类。而且,如果类不是球形的,BIRCH不能很好的工作,因为它用了半径或直径的概念来控制聚类的边界。
BIRCH 算法的步骤如下:
(1)扫描数据集,将密集的数据点分组成为子簇,而将稀疏的数据点作为孤立点去除,并利用得到的数据总结,建立一棵初始存放于内存的 CF 树。算法试图使 CF 树在内存许可范围内尽可能详细地反映数据集的聚类信息;
(2)有选择地压缩。对初始 CF 树中的叶条目进行扫描,重建一棵更小的CF树,同时去掉多余的孤立点,并将比较密集的子簇组合成更大的子簇;
(3)采用一个己有的全局或半全局的聚类算法对 CF 树中所有跨不同节点边界的叶条目进行聚类;
(4)有选择地对聚类结果提炼。将(3)产生的簇质心作为种子,将数据点重新分配给距离其最近的种子,以得到一个新的聚类集合,从而更正了不精确的地方,提炼出更好的聚类结果。
3.2 CURE 算法
Cure(利用代表点聚类)算法是对基于代表对象方法和基于质心方法进行折中的方法。在 CURE 算法中,不是利用质心或单个代表对象点来代表一个簇,而是首先在簇中选取固定数目的,离散分布的点,用这些点反映簇的形状和范围。然后把离散的点按收缩因子α向簇的质心收缩。收缩后的离散点作为簇的代表点。两个簇的距离定义为代表点对(分别来自两个簇)距离的最小值,在 CURE 算法的每一步合并距离最近的两个簇。
CURE 算法克服了利用单个代表点或基于质心方法的缺点,可以发现非球形及大小差异较大的簇。簇的收缩(离散点的收缩)降低了CURE算法对孤立点的敏感性。
调节收缩因子α,α∈[0,1],可以让CURE发现不同形式的簇。当α=1时,CURE还原为基于质心的方法。α=0时,CURE还原为 MST(最小生成树)方法。
针对大型数据库,CURE 采用随机取样和划分两种方法的组合:一个随机样本首先被划分,每个划分被部分聚类。这些结果类然后被聚类产生希望的结果。下面步骤描述了 CURE 算法的核心:
(1)从源数据对象中抽取一个随机样本 S ;
(2)将样本 S 分割为一组划分;
(3)对每个划分进行局部范围内的聚类;
(4)剔除随机样本中的孤立点;
(5)对局部的类进行聚类。落在每个新形成的类中的代表点根据用户定义的一个收缩因子α收缩或向类中心移动。这些点代表和捕捉到了类的形状;
(6)用相应的类标签来标记整个数据集合。
对于容量为 n 的样本,CURE 算法的最差时间复杂度是O(n2log n) .当数据点维数较低时,时间复杂度可减少到O(n2) .该算法仅对数据库扫描一遍,其空间复杂度为O(n) .
3.3 ROCK 算法
ROCK 算法是介于基于邻居方法和基于链接方法之间的一种相似度计算方法。使用 ROCK 算法首先需要求出数据点中所有数据的全部邻居,并求出数据点中所有数据对应的所有链接。
在得到上述初始化值之后,开始进行迭代聚类过程,迭代过程中每次迭代合并的类是通过如下的最优函数来决定的。其中,Ci ,C j分别表示两个类别,ni, nj分别表示两个类别的大小, f(θ)表示输入参数,link(C i, C j)表示类Ci 与Cj 的交叉链接数目,
这样保证 ROCK 算法在聚类过程中每次迭代合并的都是最优值最大的两个类。除了上述与 CURE 算法具有较显著的不同之外,ROCK 算法的主要流程与 CURE算法基本一致。类似地,ROCK 算法的主要思想除了与 CURE 算法思想的第二点、第四点不同之外,其余基本与 CURE 算法一致。
3.4 Chameleon 算法
Chameleon 算法也是一种层次聚类算法,且是一种聚合层次聚类算法。与基本的聚合层次聚类不同的是,该算法在合并两个类别时,采用精度更高的标准来提高聚类的质量。具体地说:该算法在判定两个类别是否进行合并时,会综合考虑互连性和近似度,尤其会考虑类内部的内在特征。该算法的上述特点使得新类能自动地适应被合并的类的内部特征,从而具有发现、构造任意大小类的能力。 与 CURE 和 DBSCAN 相比,Chameleon 算法在发现高质量的任意形状的簇方面能力更强。不过,在处理n个对象的高维数据时,算法的最坏复杂度已经达到O(n2) .
《来源科技文献,经本人分析整理,以技术会友,广交天下朋友》
石显:Chameleon 算法及其改进zhuanlan.zhihu.com