人脸识别-论文阅读-ArcFace及其由来（SphereFace、CosFace）

ArcFace（建议大家去看论文的第一版）是现在最常用的人脸识别算法，它从softmax、SphereFace和CosFace发展过来，这里就详述一下arcface算法和其发展过程。

图1

ArcFace发展过程

随着深度学习人脸识别的发展，现在人脸识别的主要思想是在网络学习的过程中增大类间差距（inter-class）的同时减小类内差距（intra-class）。

Softmax

Softmax是最常用的分类损失函数：
$$L=-\frac{1}{N}\sum _{i=1}^N\log (\frac{e^{W_{y_i}^T{x}_i+b_{y_i}}}{{\sum }_{j=1}^n{e}^{W_j^T{x}_i+b_j}})\text{\hspace{1em}(1)}$$
其中$x\in R^d$表示第i个样本中真值为y_i的深度特征，在常见的人脸识别算法中，x的特征维度一般是512维；$W_j\in R^d$ 是权重$W\in R^{d\times n}$（通常为FC层）第j个列向量，$b_j\in R^n$是偏置项；batch size和分类数目分别是N和n；对于第i个类来说，其feature embedding（嵌入特征）即为$W_i^{T}x+b_i$

softmax损失经常运用在较早的人脸识别中，但是它并没有显式地优化feature embeding从而使类间距增大和类内距减小，使得人脸识别结果并不理想。

SphereFace

SphereFace是首个将人脸识别的特征空间转换到超球面角度特征空间的算法。对于（1）式中的feature embedding（$W_i^{T}x+b_i$），由向量的乘法可以转换成$||W_i^T||||x||\cos ({\theta }_i)+b_i$，其中${\theta }_i$是W_i和x之间的角度。当将权重W_i使用L2标准化和将偏置项置零后，得到的feature embedding为$||x||\cos ({\theta }_i)$。因为在所有的权重都共享输入特征x，所以最终的分类结果的不同只跟$\theta$有关。在训练过程中，上述修改的softmax损失促使第i类的特征之间有更小的角度、与其他类之间的特征有更大的角度，从而使得分类训练更加有效。这时的修改后的softmax形式如下：
$$L=-\frac{1}{N}\sum _{i=1}^N\log (\frac{e^{||x_i||\cos ({\theta }_{y_i,i})}}{{\sum }_{j=1}^n{e}^{||x_i||\cos ({\theta }_{j,i})}}\text{\hspace{1em}(2)}$$
虽然上述损失能将特征映射到角度特征空间中，但是这些特征之间并没有区分性，即$\cos ({\theta }_i)>\cos ({\theta }_j)$来学习第i类比所有的j类角度大，但是在学习的过程中对于正确的i类来说，其角度与其他的所有类没有任何区别。所以，SphereFace加入angular marin（角度惩罚项）m从而增强损失函数的区分能力，对于正确的i类来说，使$\cos (m{\theta }_i)>\cos ({\theta }_j)$，所以（2）式就改为：
$$L=-\frac{1}{N}\sum _{i=1}^N\log (\frac{e^{||x_i||\cos (m{\theta }_{y_i,i})}}{e^{||x_i||\cos (m{\theta }_{y_i,i})}+{\sum }_{j=1,j\ne y_i}^n{e}^{||x_i||\cos ({\theta }_{j,i})}}\text{\hspace{1em}(3)}$$
SphereFace的loss方式使得CNN可以在角度空间内学习人脸特征，同时由于W_i标准化和偏置项置零，网络的预测只与输入特征x和每个类的权重W_i角度有关，所以当x与W_i的夹角${\theta }_i$比其他所有的W_j的夹角小时，x被分类到第i类。

在论文后续的内容中，证明了当处于多类分类的时候，惩罚项m至少要大于3，在后续的实验中，m=4。

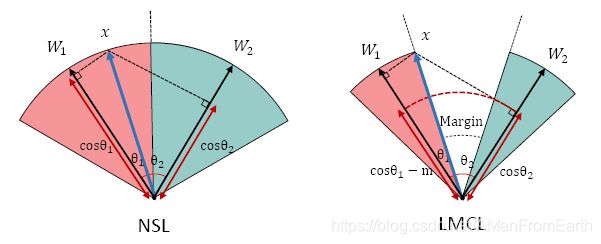
对于2分类来说，决策边界如图1所示。

CosFace

虽然SphereFace的立意很好，但是由于cosine函数是非单调函数，使得$\cos (m{\theta }_i)>\cos ({\theta }_j)$很难优化，在原文中必须加上原softmax才能稳定训练。同时，惩罚项m与$\theta$关联密切，使得不同的类有不同的间隔，导致在决策空间中有些类间距比其他类间距要大得多。

根据以上问题，CosFace提出了Large margin cosin loss(LMCL)。

在SphereFace使用L2-norm使||W_i|| = 1的基础上，CosFace更进一步使用L2-norm并rescale使||x|| = s。论文中给出的原因如下：

1. 原始的softmax函数隐式地同时学习欧式空间（L2-norm）和cosine角度。简单样本的可变的L2-norm会比难样本大得多从而弥补较小的角度差距；相反，CosFace将W和x其标准化后，类与类之间就有了相同的L2-norm，促使网络学习只依靠于cosine角度值来增加分辨能力；
2. 在学习过程中，如果使用$||x_i||\cos ({\theta }_i)>||x_i||\cos ({\theta }_j)$时，假如$\cos ({\theta }_i)<\cos ({\theta }_j)$，损失函数会要求减小||x||使得loss降低，不利于网络性能；
3. s需要设置成一个较大的数值使得在Loss较小的时候能继续下降。
4. （非原文给出的）有些模糊的人脸特征x比较小，若不进行norm则反向传播的梯度较小，进行了norm之后将其与其他人脸特征放到同样的尺度下，梯度增大了，算是一种间接的难样本加权方法。

所以（2）式就成了：
$$L=-\frac{1}{N}\sum _{i=1}^N\log (\frac{e^{s\cos ({\theta }_{y_i,i})}}{{\sum }_{j=1}^n{e}^{s\cos ({\theta }_{j,i})}}\text{\hspace{1em}(4)}$$
由于上述标准化操作移除了径向中的其他变量，使得网络学习的特征分散在角度空间中。CosFace论文中称（4）式为Normalized version of Softmax Loss(NSL)。

但是NSL和（2）式一样并没有使得类间更易区分，所以需要增加惩罚项。CosFace添加惩罚项的方式是使$\cos ({\theta }_i)-m>\cos ({\theta }_j)$，所以LMCL的形式如下：
$$L=-\frac{1}{N}\sum _{i=1}^N\log (\frac{e^{s(\cos ({\theta }_{y_i,i})-m)}}{e^{s(\cos ({\theta }_{y_i,i})-m)}+{\sum }_{j=1,j\ne y_i}^n{e}^{s\cos ({\theta }_{j,i})}}\text{\hspace{1em}(5)}$$
其二分类决策边界如图1所示，相对于NSL的分类边界如下图所示：

论文后续给出了s和m的设置方法：
$$s\ge \frac{C-1}{C}\log \frac{(C-1)P_W}{1-P_W}$$
其中C是分类数目，P_W是期望类中心的最小后验概率（即W）。

ArcFace

在CosFace的基础上，ArcFace，将惩罚项由cosine函数外移到了函数内，在训练稳定的同时更进一步地提升了人脸识别网络的辨别能力。

如下图所示，在进行特征x和权重W标准化之后，它们之间的相乘等价于cosine距离$\cos (\theta )$。对其使用arc-cosine方程来计算特征和权重之间的角度$\theta$，然后添加一个额外的角度上的加的惩罚项m得到$\theta +m$，接着对其使用cosine函数得到$\cos (\theta +m)$，在之后进行re-scale（即按照CosFace中的方式得到$s\cos (\theta +m)$），最后送入softmax损失函数中。

ArcFace的公式如下：
$$L=-\frac{1}{N}\sum _{i=1}^N\log (\frac{e^{s\cos ({\theta }_{y_i,i}+m)}}{e^{s\cos ({\theta }_{y_i,i}+m)}+{\sum }_{j=1,j\ne y_i}^n{e}^{s\cos ({\theta }_{j,i})}}\text{\hspace{1em}(6)}$$
下图是ArcFace的几何解释，不同的颜色表示特征空间中不同的类。可以看出，通过使用惩罚项m，可以压缩类内角度范围，同时使类间的边缘有一个间隔。

ArcFace优点如下：

1. 直接在标准化后的超球面通过增加类间角度的距离优化网络的分辨能力，非常直观的展现了如何优化特征和权重之间夹角；
2. 代码实现较为简单，几行代码即可；
3. 训练过程中增加的计算量很少。

实现

原文给出了MxNet的伪代码如下图：

这里结合github上开源的pytorch代码解读一下：

class ArcMarginProduct(nn.Module):
    r"""Implement of large margin arc distance: :
        Args:
            in_features: size of each input sample
            out_features: size of each output sample
            s: norm of input feature
            m: margin
            cos(theta + m)
        """
    def __init__(self, in_features, out_features, s=30.0, m=0.50, easy_margin=False):
        super(ArcMarginProduct, self).__init__()
        self.in_features = in_features #输入特征维度，一般是512
        self.out_features = out_features #输出维度，是类别数目
        self.s = s #re-scale
        self.m = m #角度惩罚项
        self.weight = Parameter(torch.FloatTensor(out_features, in_features)) #权重矩阵
        nn.init.xavier_uniform_(self.weight) #权重矩阵初始化

        self.easy_margin = easy_margin
        self.cos_m = math.cos(m)
        self.sin_m = math.sin(m)
        self.th = math.cos(math.pi - m)
        self.mm = math.sin(math.pi - m) * m

    def forward(self, input, label):
        # --------------------------- cos(theta) & phi(theta) ---------------------------
        # 对应伪代码中的1、2、3行：输入x标准化、输入W标准化和它们之间进行FC层得到cos(theta)
        cosine = F.linear(F.normalize(input), F.normalize(self.weight))
        # 计算sin(theta)
        sine = torch.sqrt((1.0 - torch.pow(cosine, 2)).clamp(0, 1))
        # 对应伪代码中的5、6行：计算cos(theta+m) = cos(theta)cos(m) - sin(theta)sin(m)
        phi = cosine * self.cos_m - sine * self.sin_m
        if self.easy_margin:
            phi = torch.where(cosine > 0, phi, cosine)
        else:
            # 当cos(theta)>cos(pi-m)时，phi=cos(theta)-sin(pi-m)*m
            phi = torch.where(cosine > self.th, phi, cosine - self.mm)
        # --------------------------- convert label to one-hot ---------------------------
        # 对应伪代码中的7行：对label形式进行转换，假设batch为2、有3类的话，即将label从[1,2]转换成[[0,1,0],[0,0,1]]
        one_hot = torch.zeros(cosine.size(), device='cuda')
        one_hot.scatter_(1, label.view(-1, 1).long(), 1)
        # 对应伪代码中的8行：计算公式(6)
        # -------------torch.where(out_i = {x_i if condition_i else y_i) -------------
        output = (one_hot * phi) + ((1.0 - one_hot) * cosine)  # you can use torch.where if your torch.__version__ is 0.4
        # 对应伪代码中的9行，进行re-scale
        output *= self.s

        return output

与Softmax、SphereFace和CosFace比较

与softmax对比

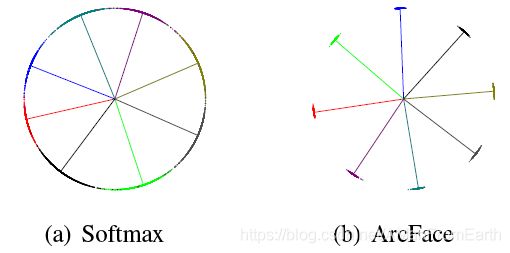
论文分别使用softmax和ArcFace训练了8个ID的人脸，如下图所示，其中点表示每个样本、线表示每个ID的中心方向

可以看出，softmax的类之间的决策边界并未明显分开，边缘有明显接触。而ArcFace中相邻类之间有着十分明显的间隔，由于人脸特征标准化，所有的特征都被转到角度空间中；同时由于角度惩罚项m的加入，各个类之间间隔明显。

与SphereFace和CosFace对比

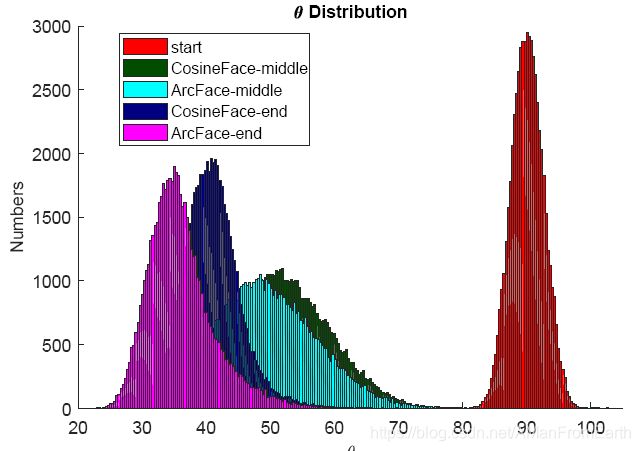
下图展示了在训练过程中CosFace和ArcFace角度$\theta$的变化，可以看出，在初始化分布相同的情况下，无论是训练过程中还是训练结束，ArcFace的角度分布都在CosFace左边（即角度更小），证明了ArcFace更能压缩类内角度范围和增大类间角度间隔，即网络的分辨能力更强。

论文展示了softmax、SphereFace、CosFace和ArcFace在特征与目标中心角度范围[20°,100°]下的logit分布，在下图（b）中，ArcFace比其他3个损失的曲线都要低，表示ArcFace相对其他loss施加了更加严格的惩罚项。之所以只展示这个角度范围，是疑问ArcFace训练过程中发现，角度最终分布在[20°,100°]，如下图（a）。

它们之间的二分类决策边界如图1所示。

实验

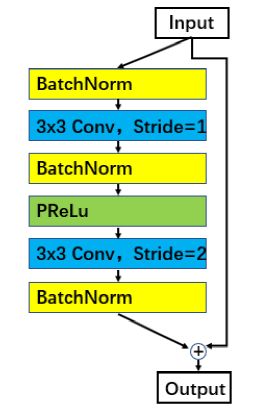
ArcFace论文中修改了原ResNet-basicblock，称为IRBlock（improved residual unit），如下图：

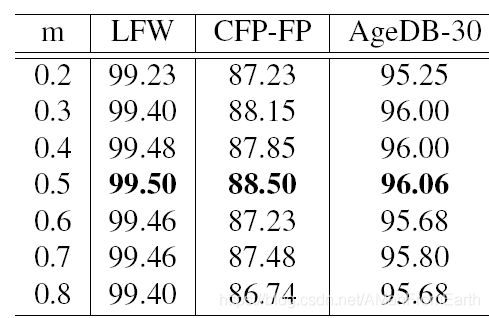
不同m取值的影响：

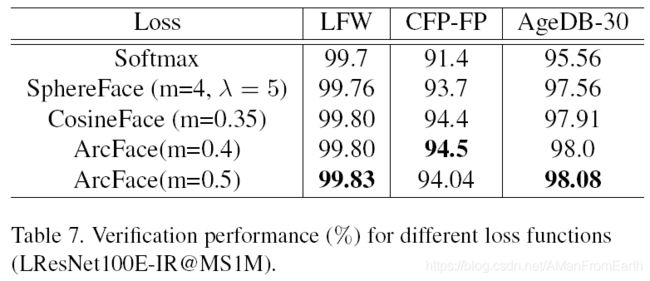
与其他loss的对比结果：

以上就是本文的全部内容。