3D视觉笔记(1) - 双目视觉三维测量原理
中心投影模型(针孔相机模型)
在之前的笔记中,有讨论过针孔相机的模型和世界坐标系统的点如何投影到图像坐标系中。参考如下两篇笔记:
几何角度理解相机成像过程_亦枫Leonlew的博客-CSDN博客本笔记从几何角度来理解相机的成像过程,我们生活在三维世界中,相机所捕捉到的画面是2D的,3D空间中的点是如何投影到2D平面的过程是本笔记关注的。这个过程其实和3D游戏中的透视投影过程是一样的。本笔记只要知道矩阵乘法的知识就可以理解。https://blog.csdn.net/vivo01/article/details/128252788?spm=1001.2014.3001.5502相机标定笔记(1) -- 相机模型_亦枫Leonlew的博客-CSDN博客我们知道,相机的图像是三维世界到2D平面的一个投影。仅从这个2D图像来看,我们无法得知图像中的物体在真实物理世界中有多大,距离相机的距离有多远。那么我们有没有办法从这个2D的图片结合相机的参数获得这些信息呢?答案是有的,方法有很多种,比如双目视觉技术,可以用来恢复三维信息。如何恢复精确的3D物体?图像失真(比如镜头畸变)了如何恢复?先用数学表达式描述对相机成像过程建模,然后通过数学表达式计算恢复这些信息。https://blog.csdn.net/vivo01/article/details/128471170?spm=1001.2014.3001.5502 在本笔记中,我们首先来搞清楚一件事情,为什么单目相机无法测得深度(这句话不太严谨,限定为单目相机位置不变的情况下,所拍摄的一张图,从这张图无法得到深度信息)?
来看针孔相机模型示意图:
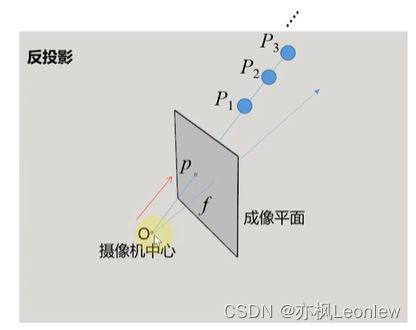
在3D世界中的一个点P,经过投影后在相机的成像平面上形成一个像点p,这个过程(3D到2D的投影)是确定的。但是反过来,我们知道成像平面上的一个像点p,想要知道3D世界中的点P的信息,则P的位置是无法确定的。根据一副图像中的一个2D像点p,加上相机的中心点O,我们只能确定出一条射线,如下图:
我们要找的P点,在Op延长线上的任意位置都有可能,这些点如P1,P2,P3经过投影都对应到相机成像平面的p点。
为了能够确定出点P的位置,我们可以使用两个相机,拍摄两幅图。这样就能发出两条射线,如下图所示:
这样两个相机的两条射线的交点就能确定目标点的3D位置。这是双目立体视觉系统进行3D测量的基本原理。
理想的双目系统模型
理想的双目系统中,两个相机的焦距f完全相同,左右两个相机处于同一个平面内,光轴平行。
首先来看两个概念:B - 基线长度,指的是左右两个相机关心之间的距离, D - 视差,表示P点投影到左右相机成像平面上两点的x坐标之间的差值![]() 。
。
如下图,假设P点的坐标位置是(X,Y,Z):
在之前笔记中,我们知道了相机的图像坐标系以光轴和成像平面的交点为原点。因此在上图中,左相机的![]() 值为正,右相机的
值为正,右相机的![]() 为负,。
为负,。
图中标注了两个红色箭头,每个红色箭头所覆盖的两个一大一小的三角形是相似的。对于左相机的两个相似三角形,我们可以得到:
同理,对于右相机来说,可以得到:
对于Y来说,同样根据相似三角形可以得到(这里不再画出YZ平面的视图,感兴趣的朋友自行推导):
根据式1和式2,我们可以解出X:
将X代入到式1中,可以解出Z:
一般来说Z会先用这个式子求解,然后用Z和f去表示X和Y,因此X为:
对于Y来说,将Z代入利用类似的方法也可以求解出来:
综上,我们就可以通过左右两个相机的像点来推出P点的三维坐标了。
对于P'和P‘’这两个位置来说,使用同样推导过程可以得出同样的结论,感兴趣的朋友自行推导,不再赘述。
如何确定左右两幅图的点对应关系
前面小节说明了双目相机是如何根据两个点来演算出3D世界中的点P的。但有个前提是,我们知道这两个点是3D世界中的点P投影到左右相机成像平面上的点。也就是说这两个点对应3D世界中的同一个物点。
对于计算机来说,它只是得到了两幅图,但两幅图中的两个点是否对应到3D世界中的同一个点来说,它是不知道的,因此我们需要一些匹配算法来做这个事情。
特征匹配
在计算机视觉领域,计算机识别点对应关系的方法通常是特征匹配(Feature Matching)。 下图展示了使用ORB特征描述符(一种找点对应关系的方法)进行匹配后的结果。
一种最简单的用于找到点对应关系的方法是找到临近像素信息都类似的像素,假设两个像素点一定范围内的邻居像素相似度很高,那么就认为这两个点是两幅图中对应的点。比如对于下图左相机的一个点,找出这个点和其邻居像素的信息作为比对信息,在右图中进行搜索匹配。
但这种暴力搜索的方法有两个比较蛋疼的问题。如上图所示,第一个问题是搜索的空间太大,假设我们要找左图用蓝色线框所标记的点,在右图搜索时要去搜索的范围没有任何指导性的算法去缩小这个范围。第二个问题是我们从比对结果可以看到,对于左图中的一个像素,右图中存在多个匹配结果。显然这种方法要找到真正的匹配是非常低效并且困难的。
有没有办法缩小搜索空间呢?其实是有的,可以使用对极几何(epipolar geometry)的知识来做到这一点。
对极几何描述了左右两个相机所拍摄的两幅图之间固有的对应关系,是立体视觉研究中重要的数学方法。
对极几何在立体匹配中的应用
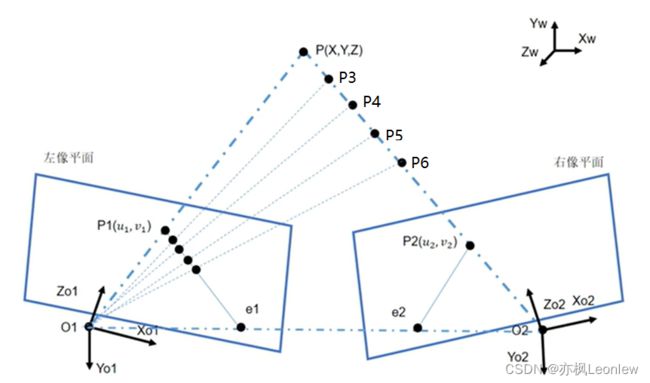
以上图为例来讲解重要的概念:
基线(baseline):左右相机中心点O1,O2的连线
极平面(epipolar plane):上图中使用射线O1P1加上基线O1O2可以确定出一个平面O1O2P1。这个平面区域可以随着射线O1P1方向延伸,比如延伸到P点后,这个平面就是O1O2P,我们称这个平面为极平面。
极点(epipole): e1,e2这两个点称为极点。e1是O2在左像平面的投影,e2是O1在右像平面的投影。
极线(epipolar line):极平面和两个成像平面相交的线称为极线。如上图的e1P1,e2P2。
知道了上面的基本概念后,我们来看一个立体视觉中经常会听到的概念,极线约束。
极线约束
极线约束所要说的事情简单来说就是,一个成像平面A中的一个点在另一个成像平面B中的位置一定在极平面与成像平面B相交的极线上。还是以前面的图为例,假设我们知道右像平面中的P2点的坐标,我们想找到P2在左像平面中和其对应的点的坐标,我们就沿着e1P1这条线进行搜索就好了。
我们最终要确定的位置点是P1,对应3D世界中的点P。点P和P3,P4,P5,P6都在射线O2P2延长线上,因此它们在右像平面上的投影都对应P2这个点。我们把P,P3,P4,P5,P6这几个点投影到左像平面上,由于这些点都共面(极平面),这几个点一定会投影到极线e1P1上。反过来,假设我们知道P1,想要在右像上搜索P2,原理也是类似的。
上面的图基本是实际的双目相机中的例子,但这个和我们所说的理想双目系统的模型还是有差异。上图的例子中,极线是倾斜的,在两个维度上(x,y)上都有涉及。而理想的双目系统模型中,我们可以知道,左图中的某个点P,在右图中一定和P点处于同一行的位置,这样在做搜索时,就能去掉一个维度的信息,更加简单高效。那么有没有办法将真实的非理想的双目系统经过变换变成理想的双目系统呢?答案当然也是有的,就是接下来要介绍的极线校正的概念。
极线校正
极线校正最终目的是让极线对共线且平行于像平面的某个坐标轴,通常是水平轴,经过极线校正后,建立了新的左右立体成像平面对。校正完成后,同一匹配点对,在两个成像平面中处于同一行内,也就是说它们在两个成像平面上只有水平位置的差异,这个差异称为视差(disparity)。
下图是一个实际的例子,可以更加直观的看到校正前后的差别。
上图(a)是为进行校正时,极线(黑色)的分布情况。(b)则是进行校正之后的样子。
想要进一步了解极线校正细节,可以参考这篇文章:
立体视觉入门指南(6):对级约束与Fusiello法极线校正 - 知乎亲爱的同学们,我们的世界是3D世界,我们的双眼能够观测三维信息,帮助我们感知距离,导航避障,从而翱翔于天地之间。而当今世界是智能化的世界,我们的科学家们探索各种机器智能技术,让机器能够拥有人类的三维感…![]() https://zhuanlan.zhihu.com/p/466758105
https://zhuanlan.zhihu.com/p/466758105