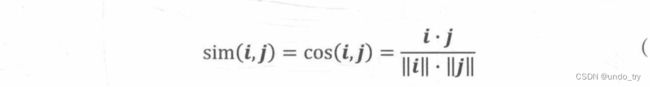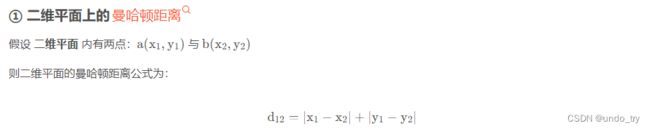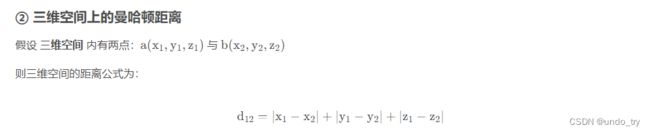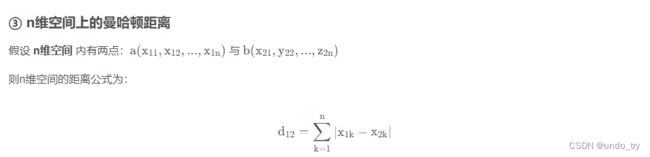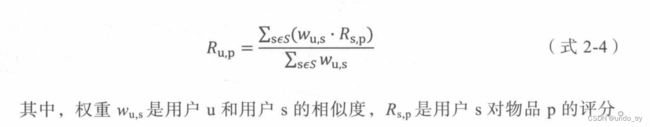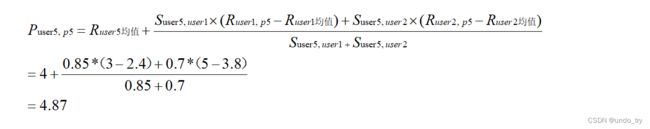传统推荐模型(一)协同过滤算法_UserCF和ItemCF
传统推荐模型(一)协同过滤算法_UserCF
1、UserCF
协同过滤就是协同大家的反馈、评价和意见一起对海量的信息进行过滤,从中筛选出目标用户可能感兴趣的信息的推荐过程。
| 物品1 | 物品2 | 物品3 | 物品4 | 物品5 | |
|---|---|---|---|---|---|
| 用户1 | 3 | 1 | 2 | 3 | 3 |
| 用户2 | 4 | 3 | 4 | 3 | 5 |
| 用户3 | 3 | 3 | 1 | 5 | 4 |
| 用户4 | 1 | 5 | 5 | 2 | 1 |
| 用户5 | 5 | 3 | 4 | 4 | ? |
(1) 电商网站的商品库里一共有5件商品:物品1、物品2、物品3、物品4、物品5
(2) 用户5 访问该电商网站,电商网站的推荐系统需要决定是否推荐物品5给用户5。换言之,推荐系统需要预测用户5是否喜欢物品5。为了进行这项预测,可以利用的数据有用户5对其他商品的历史评价数据,以及其他用户对这些商品的历史评价数据。
(3) 将用户对物品评分数据写成上图的形式(称为共现矩阵),生成共现矩阵之后,推荐问题就转换成了预测矩阵中问号元素所示的值的问题。既然是“协同”过滤,用户理应考虑与自己兴趣相似的用户的意见。因此,预测的第一步就是找到与用户5兴趣最相似的 n (Top n 用户这里的n是一个超参数)个用户,然后综合相似用户对物品5的评价,得出用户5对物品5评价的预测。
因此,需要共现矩阵中,需要找到与用户5最相似的n个用户。在协同过滤的过程中,用户相似度的计算是算法中最关键的一步。计算用户i和用户j相似度问题,就是计算用户向量i和用户向量j之间的相似度。
(1)相似度的计算方式
1、杰卡德相似度(Jaccard)
这个是衡量两个集合的相似度一种指标。 两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示
具体可以参考:杰卡德相似度(Jaccard)详解及在UserCF中的应用
2、余弦相似度
余弦相似度(Cosine Similarity)衡量了用户向量i和用户向量j之间的向量夹角大小。显然,夹角越小,证明余弦相似度越大,两个用户越相似。
计算用户5和用户1的余弦相似性
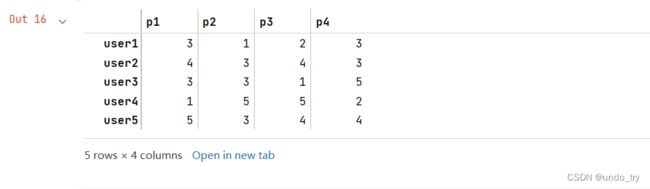
用户向量如下:
user1(3,1,2,3) user2(4,3,4,3) user3(3,3,1,5) user4(1,5,5,2) user5 (5,3,4,4)
users = ["user1", "user2", "user3", "user4", "user5"]
items = ["p1", "p2", "p3", "p4"]
#用户对物品评分数据集
datasets = [
[3,1,2,3],
[4,3,4,3],
[3,3,1,5],
[1,5,5,2],
[5,3,4,4]
]
df = pd.DataFrame(datasets,columns=items,index=users)
df
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(
[df.loc['user5'],df.loc['user1']]
)
对于[评分数据不规范]的时候,也就是说,存在有的用户喜欢打高分,有的用户喜欢打低分情况的时候,有的用户喜欢乱打分的情况,这时候consine相似度算出来的结果可能就不是那么准确了,可以考虑皮尔逊相关系数.
3、皮尔逊相关系数
相比余弦相似度,皮尔逊相关系数通过使用用户平均分对各独立评分进行修正,减小了用户评分偏置的影响。
简单的说,其实pearson做的就是把两个向量都减去他们的均值,然后再计算consine值。
计算用户5和用户1的皮尔逊相关系数
用户向量如下:
user1(3,1,2,3) user2(4,3,4,3) user3(3,3,1,5) user4(1,5,5,2) user5 (5,3,4,4)
用户5的均值为4,用户1的均值为2.25
向量减去均值为
user1(1,-1,0,0) user5 (0.75,-1.25,0.25,0.75)
计算这两个新向量的余弦相似度,和上面计算过程一致,可以得到结果为0.852
np.corrcoef(
df.loc['user5'],
df.loc['user1']
)
基于皮尔逊系数的思路,还可以通过引入物品平均分的方式,减少物品评分偏置对结果的影响。
4、欧式距离、曼哈顿距离、马氏距离
欧式距离
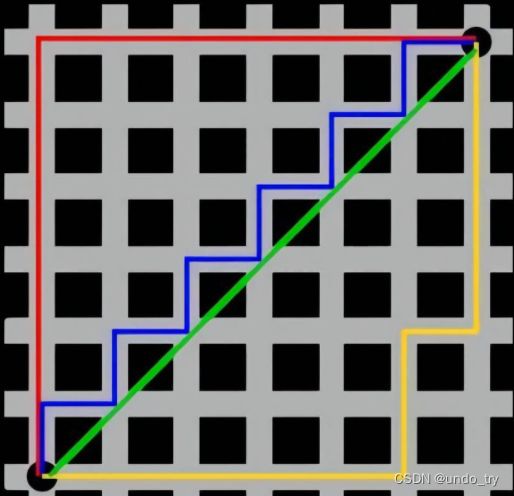
曼哈顿距离
曼哈顿距离,不能像 绿线(/) 一样,横穿建筑,而是需要和其它三条线一样, 穿过大街小巷。
马氏距离
可以参考: https://blog.csdn.net/weixin_39910711/article/details/113985520
(2)基于User的协同过滤(UserCF)
1、计算用户5和其他用户的相似度
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
#用户对物品评分数据集
datasets = [
[3,1,2,3],
[4,3,4,3],
[3,3,1,5],
[1,5,5,2],
[5,3,4,4]
]
user_similar = cosine_similarity(
datasets
)
user_similar = pd.DataFrame(user_similar,columns=users,index=users)
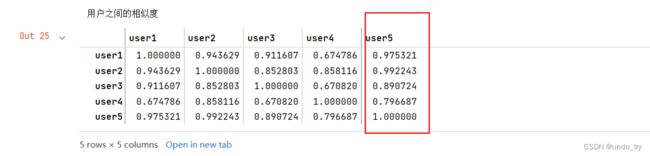
print("用户之间的余弦相似度")
user_similar
user_similar = np.corrcoef(
datasets
)
user_similar = pd.DataFrame(user_similar,columns=users,index=users)
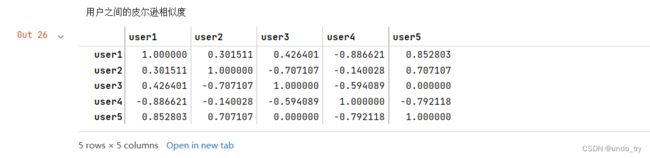
print("用户之间的皮尔逊相似度")
user_similar
2、根据相似度用户计算用户5对物品5的最终得分
在获得 Top n 相似用户之后,利用 Top n 用户生成最终推荐结果的过程如下. 假设“目标用户与其相似用户的喜好是相似的”,可根据相似用户的已有评价对目标用户的偏好进行预测。
方式一:
最常用的方式是利用 [用户相似度] 和[相似用户的评价]的加权平均获得目标用户的评价预测
假设n为2,那么用余弦相似度计算方式如下:
方式二:
3、根据用户评分对用户进行推荐
可以定一个阈值,预测评分超过阈值,即可推荐给用户,例如本例定阈值为3,超过阈值3,因此可以推荐物品5给用户5.
(3)基于User的协同过滤(UserCF)缺点
以上介绍的协同过滤算法基于用户相似度进行推荐,因此也被称为基于用户的协同过滤 (UserCF),它符合人们直觉上的兴趣相似的朋友喜欢的物品,我也喜欢的思想,但从技术的角度,它也存在一些缺点,主要包括以下两点
(1)在互联网应用的场景下,用户数往往远大于物品数,而 UserCF 需要维护用户相似度矩阵以便快速找出 Top n 相似用户。该用户相似度矩阵的存储开销非常大,而且随着业务的发展,用户数的增长会导致用户相似度矩阵的存储空间以 n的平方 的速度快速增长,这是在线存储系统难以承受的扩展速度
(2)用户的历史数据向量往往非常稀疏,对于只有几次购买或者点击行为的用户来说,找到相似用户的准确度是非常低的,这导致 UserCF 不适用于那些正反馈获取较困难的应用场景 (如酒店预定、大件商品购买等低频应用)。
2、ItemCF
由于UserCF技术上的两点缺陷导致很多电商平台并没有采用这种算法,而是采用了ItemCF算法实现最初的推荐系统。
如果想知道用户5对物品5打多少分,基于物品的协同过滤算法会这么做:
-
首先计算一下物品5和物品1,2,3,4之间的相似性(它们也是向量的形式,每一列的值就是它们的向量表示,
因为ltemCF认为物品a和物品c具有很大的相似度是因为喜欢物品a的用户大都喜欢物品c,所以就可以基于每个用户对该物品的打分或者说喜欢程度来向量化物品) -
找出与物品5最相近的n个物品
-
根据用户5对最相近的n个物品的打分去计算对物品5的打分情况
| 物品1 | 物品2 | 物品3 | 物品4 | 物品5 | |
|---|---|---|---|---|---|
| 用户1 | 3 | 1 | 2 | 3 | 3 |
| 用户2 | 4 | 3 | 4 | 3 | 5 |
| 用户3 | 3 | 3 | 1 | 5 | 4 |
| 用户4 | 1 | 5 | 5 | 2 | 1 |
| 用户5 | 5 | 3 | 4 | 4 | ? |
物品向量如下:
p1(3,4,3,1) p2(1,3,3,5) p3(2,4,1,5) p4(3,3,5,2) p5 (3,5,4,1)
直接计算余弦相似度和皮尔逊相似度
items = [
[3,4,3,1] ,
[1,3,3,5] ,
[2,4,1,5] ,
[3,3,5,2] ,
[3,5,4,1]
]
items_index = ["p1", "p2", "p3", "p4", "p5"]
item_similar = cosine_similarity(
items
)
item_similar = pd.DataFrame(item_similar,columns=items_index,index=items_index)
print("物品之间的余弦相似度")
item_similar
item_similar = np.corrcoef(
items
)
item_similar = pd.DataFrame(item_similar,columns=items_index,index=items_index)
print("物品之间的皮尔逊相似度")
item_similar
可以看出物品1和物品4和物品5相似度高;
利用皮尔逊相似度,并利用方式2计算评分
3、UserCF和ItemCF的应用场景
-
由于 UserCF 基于用户相似度进行推荐,使其具备更强的社交特性用户能够快速得知与自己兴趣相似的人最近喜欢的是什么,即使某个兴趣点以前不在自己的兴趣范围内,也有可能通过“朋友”的动态快速更新自己的推荐列表。
这样的特点使其非常适用于新闻推荐场景。因为新闻本身的兴趣点往往是分散的,相比用户对不同新闻的兴趣偏好,新闻的及时性、热点性往往是其更重要的属性,而UserCF 正适用于发现热点,以及跟踪热点的趋势; -
ItemCF 更适用于兴趣变化较为稳定的应用,比如在Amazon 的电商场景中,用户在一个时间段内更倾向于寻找一类商品,这时利用物品相似度为其推荐相关物品是契合用户动机的。在 Netflix 的视频推荐场景中,用户观看电影、电视剧的兴趣点往往比较稳定,因此利用 ItemCF 推荐风格、类型相似的视频是更合理的选择。
4、协同过滤的下一步发展
协同过滤虽然是一个非常直观而且可解释性很强的模型,但是它并不具备较强的泛化能力。存在一个比较严重的问题——热门的物品具有很强的头部效应,容易跟大量物品产生相似性;而尾部的物品由于特征向量稀疏,很少与其他物品产生相似性,导致很少被推荐。
下图计算了A、B、C、D四个物品的余弦相似度,通过物品相似度矩阵可知,A、B、C 之间的相似度均为 0,而与 A、B、C最相似的物品均为物品 D,因此在以 ItemCF 为基础构建的推荐系统中,物品D将被推荐给所有对 A、B、C 有过正反馈的用户。
但事实上,物品 D与A、B、C 相似的原因仅在于物品 D 是一件热门商品,系统无法找出 A、B、C 之间相似性的主要原因是其特征向量非常稀疏,缺乏相似性计算的直接数据。这一现象揭示了协同过滤的天然缺陷——推荐结果的头部效应较明显,处理稀疏向量的能力弱。
为解决上述问题,同时增加模型的泛化能力,矩阵分解技术被提出。该方法在协同过滤共现矩阵的基础上,使用更稠密的隐向量表示用户和物品,挖掘用户和物品的隐含兴趣和隐含特征,在一定程度上弥补了协同过滤模型处理稀疏矩阵能力不足的问题。
另外,协同过滤仅利用用户和物品的交互信息,无法有效地引入用户年龄性别、商品描述、商品分类、当前时间等一系列用户特征、物品特征和上下文特征,这无疑造成了有效信息的遗漏。 为了在推荐模型中引入这些特征,推荐系统逐渐发展到以逻辑回归模型为核心的、能够综合不同类型特征的机器学习模型的道路上。