传统推荐模型——协同过滤

---

协同过滤，Collaborative Filtering，CF，可以说是业界影响力最大、应用最广泛的模型，作为曾经推荐系统的首选模型，协同过滤基于系统中其他用户的评分或行为进行预测和推荐，分为基于用户的协同过滤和基于物品的协同过滤两种算法。

UserCF：基于用户的协同过滤

什么是CF

顾名思义，“协同过滤”就是协同大家的反馈、评价和意见一起对海量的信息进行过滤，从中筛选出目标用户可能感兴趣的信息的推荐过程。

这里用一个商品推荐的例子说明一下

此推荐过程大致可以分为6步：

1、一共有4件商品：电视、杂志、书、游戏机

2、历史上，用户$A,B,C,D,X$已经对商品有过一些访问的记录，并且留下了好评和差评的标记（对应绿色和红色）。现在需要利用用户$X$对商品的历史评价、其他用户对商品的历史评价，预测是否把电视机推荐给用户$X$

3、为便于计算，将用户和商品放到矩阵里（称为“共现矩阵”），并将好评设为1，差评设为-1，未评价设为0（如果有具体评分，如1-5星，可以将评分作为矩阵的元素值）

4、现在对于是否推荐电视机的问题转换为图中？的数值是多少。既然是协同过滤，所以应当考虑与用户$X$兴趣最相似的$n$个用户，然后综合这$n$个用户对电视机的评价，得到对于$X$和电视机交互的预测。（Top $n$用户问题，$n$是一个超参数）

5、假设选定$n=2$，可以看出，用户$B$和用户$C$与$X$最相似，所以被选为Top 2用户

6、因为用户$B$和用户$C$对电视机都是负面评价，所以预测$X$对于电视机的评价也是负面，所以不会向用户$X$推荐电视机

以上是简化的利用CF推荐的流程，其中的“用户相似”和“最终结果排序”的计算是不严谨的，这两部分如何计算将会直接影响推荐的结果。

用户相似度计算

两个用户的相似度，也就是在共现矩阵里，计算两个用户对应向量的相似度，常用方法有以下几种：

1、余弦相似度
$$\mathrm{sim}(i,j)=\cos (i,j)=\frac{\mathbf{i}\cdot \mathbf{j}}{\Vert \mathbf{i}\Vert \cdot \Vert \mathbf{j}\Vert }$$
用户$i$和$j$的向量夹角越小，余弦相似度越大，两个用户越相似

2、皮尔逊相关系数
$$\mathrm{sim}(i,j)=\frac{{\sum }_{\mathrm{p}ϵP}\left(R_{\mathrm{i},\mathrm{p}}-{\bar{R}}_{\mathrm{i}}\right)\left(R_{\mathrm{j},\mathrm{p}}-{\bar{R}}_{\mathrm{j}}\right)}{\sqrt{{\sum }_{\mathrm{p}ϵP}{\left(R_{\mathrm{i},\mathrm{p}}-{\bar{R}}_{\mathrm{i}}\right)}^2}\sqrt{{\sum }_{\mathrm{p}ϵP}{\left(R_{\mathrm{j},\mathrm{p}}-{\bar{R}}_{\mathrm{j}}\right)}^2}}$$
其中，$P$代表所有item的集合， $R_{i,p}$代表用户$i$对物品$p$的评分，${\bar{R}}_{\mathrm{i}}$代表用户$i$对所有物品的平均评分。

可以看出，加入了用户的平均分，减少了用户评分偏置的影响。

3、基于皮尔逊相关系数，将用户平均分${\bar{R}}_{\mathrm{i}}$改成物品平均分${\bar{R}}_{\mathrm{p}}$，减少物品评分偏置的影响
$$\mathrm{sim}(i,j)=\frac{{\sum }_{\mathrm{p}ϵP}\left(R_{\mathrm{i},\mathrm{p}}-\overline{R_{\mathrm{p}}}\right)\left(R_{\mathrm{j},\mathrm{p}}-\overline{R_{\mathrm{p}}}\right)}{\sqrt{{\sum }_{\mathrm{p}ϵP}{\left(R_{\mathrm{i},\mathrm{p}}-\overline{R_{\mathrm{p}}}\right)}^2}\sqrt{{\sum }_{\mathrm{p}ϵP}{\left(R_{\mathrm{j},\mathrm{p}}-\overline{R_{\mathrm{p}}}\right)}^2}}$$
理论上，任何合理的“向量相似度定义方式”都可以作为相似用户计算的标准。研究人员通过对相似度定义的改进来不断解决传统的CF存在的一些缺陷的。

最终结果的排序

在获得Top n相似用户之后，最常用的是利用用户相似度和相似用户的评价的加权平均获得最终的预测
$$R_{\mathrm{u},\mathrm{p}}=\frac{{\sum }_{\mathrm{s}ϵS}\left(w_{\mathrm{u},\mathrm{s}}\cdot R_{\mathrm{s},\mathrm{p}}\right)}{{\sum }_{\mathrm{s}ϵS}{w}_{\mathrm{u},\mathrm{s}}}\text{\hspace{1em}(4)}$$
其中，$w_{u,s}$是用户$u$和$s$的相似度，$R_{s,p}$是用户$s$对用户$p$的评分。

（4）式一次可以预测用户$U$对物品p的评分，在预测完所有物品之后，根据评分进行排序，即可得到推荐的列表。

基于用户相似度的推荐，有一个大的前提，认为“兴趣相似的朋友喜欢的物品，我也喜欢”，但从技术的角度，它也存在一些缺点：

• 在互联网应用的场景下，用户数往往远大于物品数，用户相似度矩阵的存储开销非常大，并且是以$n^2$的复杂度快速增长的。
• 用户的历史数据往往非常稀疏，对于只有几次购买或者点击行为的用户来说，找到相似用户的准确度是非常低的，这导致 UserCF 不适用于那些正反馈获取较困难的应用场景（如酒店预定、大件商品购买等低频应用）

ItemCF：基于物品的协同过滤

为避免上面提到的两个问题，常常采用ItemCF算法实现推荐系统。思想和UserCF很相似，简单来说就是如果用户A同时购买了商品1和商品2，那么说明商品1和商品2的相关度较高。当用户B也购买了商品1时，可以推断他也有购买商品2的需求。

预测对用户$X$推荐$\text{ Top }k$物品

1、基于历史数据，构建用户和物品的$m\times n$维共现矩阵

2、计算每个物品向量之间的相似度，构建$n\times n$维的物品相似度矩阵

3、获得用户$X$历史行为数据中的正反馈物品列表

4、利用物品相似度矩阵，针对正反馈物品列表，找出相似的$\text{ Top }k$ 物品

5、对$\text{ Top }k$ 物品，利用相似度的分值进行排序，生成最终的推荐列表。

对第4、5步骤举个例子，用户已经购买过商品4、5，预测推荐商品A,B,C中的哪一个。利用物品相似度矩阵，（可以利用商品4、5的评分进行加权排序），得到最终相似度评分（最下面一行）。

​ 在第5步中，如果一个物品和多个的正反馈物品相似，那么该物品最终相似度应该是多个相似度的累加：
$$R_{\mathrm{u},\mathrm{p}}=\sum _{\mathrm{h}ϵH}\left(w_{\mathrm{p},\mathrm{h}}\cdot R_{\mathrm{u},\mathrm{h}}\right)$$
其中，$H$是目标用户的正反馈物品集合。

UserCF和ItemCF的适用场景

UsercF 的最大特点是即使某个兴趣点以前不在自己的兴趣范围内，也有可能通过朋友的动态快速更新自己的推荐列表。这样的特点使其非常适用于新闻推荐场景。相比用户对不同新闻的兴趣偏好，新闻的及时性、热点性往往是其更重要的属性，而 UsercF 正适用于发现热点，以及跟踪热点的趋势。除此之外，在社交网络中 UserCF 也是一个更好的选择，可以增加用户对推荐解释的信服程度。

​ ItemCF 适用于购物网站、视频推荐等场景。原因之一是兴趣变化较为稳定，用户在一个时间段内更倾向于寻找一类商品，这时利用物品相似度为其推荐相关物品更合适；另一个原因是用户的数量远远超过物品的数量，其物品的数据相对稳定，因此计算物品的相似度时不但计算量较小，而且不必频繁更新。

CF存在的几个缺点

（1）系统开始时推荐质量较差

（2）质量取决于历史数据集

（3）数据稀疏性问题（Sparsity）

（4）系统延伸性问题（Scalability）

（5）用户提供恶意评价对系统带来的偏差

代码实践

数据集

使用ml-100k电影评分数据集中的u.data

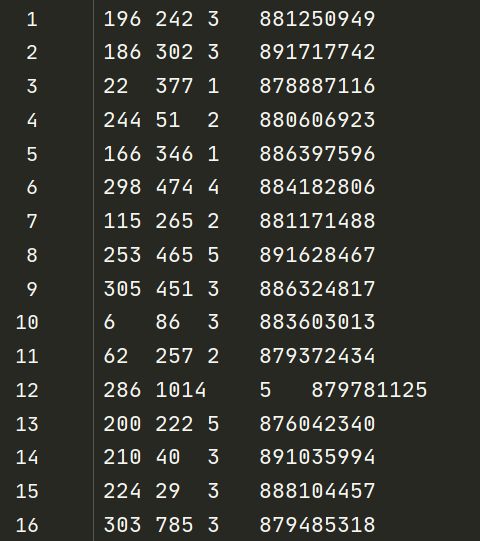
四列分别对应用户id，电影id，评分， 时间戳

总共包含943位用户，1682部电影，100000个评分，评分1—5，每个用户至少20部

Python代码

导入处理数据集

import numpy as np
import pandas as pd

# 读取u.data文件
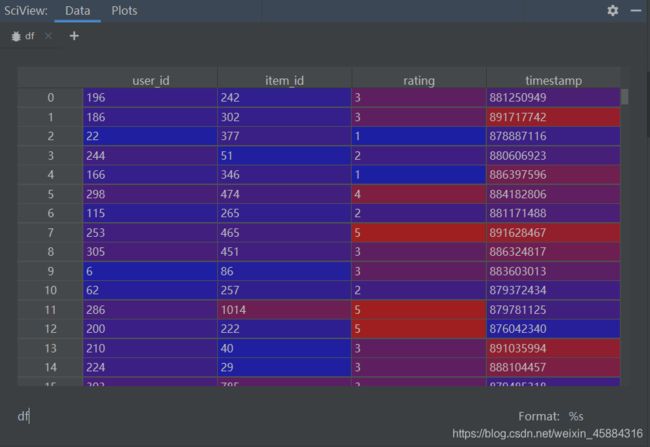
header = ['user_id', 'item_id', 'rating', 'timestamp']
df = pd.read_csv('./ml-100k/ml-100k/u.data', sep='\t', names=header)

分割训练集、测试集

from sklearn.model_selection import train_test_split
train_data, test_data = train_test_split(df, test_size=0.2)

创建uesr-item矩阵

# 计算唯一用户和电影的数量（去掉重复）
n_users = df.user_id.unique().shape[0]
n_items = df.item_id.unique().shape[0]
print('Number of users = ' + str(n_users) + ' | Number of movies = ' + str(n_items))

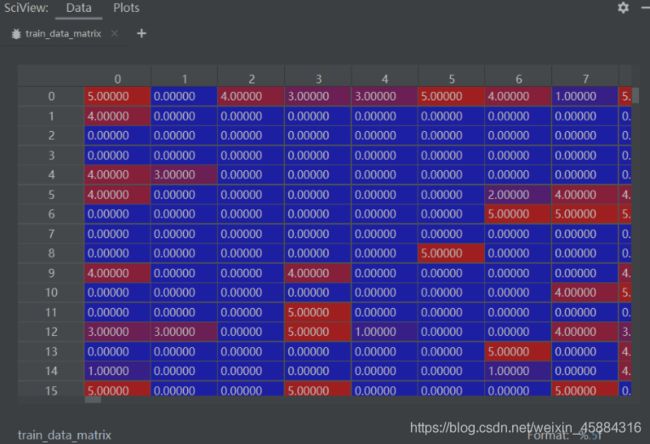
# 创建n_users × n_items维矩阵
train_data_matrix = np.zeros((n_users, n_items))
for line in train_data.itertuples():
    train_data_matrix[line[1] - 1, line[2] - 1] = line[3]
test_data_matrix = np.zeros((n_users, n_items))
for line in test_data.itertuples():
    test_data_matrix[line[1] - 1, line[2] - 1] = line[3]

通过 pairwise_distances求相似度(余弦相似度)

# 计算相似度
# 使用sklearn的pairwise_distances函数来计算余弦相似性
from sklearn.metrics.pairwise import pairwise_distances
# 计算用户相似度
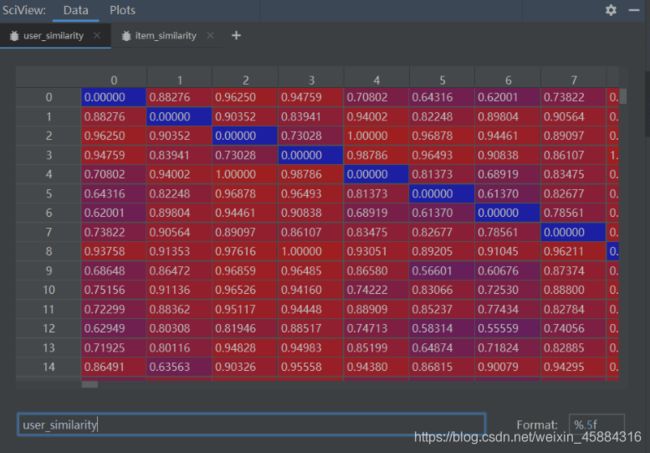
user_similarity = pairwise_distances(train_data_matrix, metric='cosine')
# 计算物品相似度
item_similarity = pairwise_distances(train_data_matrix.T, metric='cosine')

用户相似度矩阵：

商品相似度矩阵：

预测（基于用户和商品）

# ------------------------预测--------------------------------
def predict(ratings, similarity, type='user'):
    # 基于用户相似度矩阵的
    if type == 'user':
        # 求每一行(user)的平均值
        mean_user_rating = ratings.mean(axis=1)
        ratings_diff = (ratings - mean_user_rating[:, np.newaxis]) # np.newaxis自动补充维度
        pred = mean_user_rating[:, np.newaxis] + similarity.dot(ratings_diff) / np.array(
            [np.abs(similarity).sum(axis=1)]).T

    # 基于物品相似度矩阵
    elif type == 'item':
        pred = ratings.dot(similarity) / np.array([np.abs(similarity).sum(axis=1)])
    return pred

# 预测结果
user_prediction = predict(train_data_matrix, user_similarity, type='user')
item_prediction = predict(train_data_matrix, item_similarity, type='item')

mean_user_rating：user向量的平均值

ratings_diff：U-I矩阵减去每个user的平均值

pred：预测结果

评价结果

协同过滤 - 简书

王喆《深度学习推荐系统》
协同过滤算法原理分析