【图神经网络】图神经网络(GNN)学习笔记:GAT
图神经网络GNN学习笔记:图注意力网络GAT
- 图注意力网络简介
- 注意力机制是什么?
- 图注意力层(Graph Attentional Layer)
- 多头图注意力层
- 从GNN到GCN再到GAT
- 参考资料
图注意力网络(Graph Attention Networks, GAT),处理的是图结构数据。它通过注意力机制(Attention Mechanism)来对邻居节点做聚合操作,实现了对不同邻居权重的自适应分配,大大提高了图神经网络的表达能力。
图注意力网络简介
它与先前方法不同的是,它使用了masked self-attention层。原来的图卷积网络所存在的问题需要使用预先构建好的图。而在本文模型中,图中的每个节点可以根据邻域节点的特征,为其分配不同的权值。GAT结构很简单,功能很强大,模型易于解释。文章的实验证明,GAT模型可以有效地适用于基于图的归纳学习问题与转导学习问题。
图注意力网络将注意力机制引入到基于空间域的图神经网络,与之前介绍了基于谱域的图卷积神经网络不同,图注意力网络不需要使用拉普拉斯等矩阵进行复杂的计算,仅是通过一阶邻居节点的表征来更新节点特征,所以算法原理从理解上较为简单。
图注意力网络优化了图卷积神经网络的几个缺陷:
- 图卷积神经网络擅长处理transductive任务,无法完成inductive任务。图卷积神经网络进行图卷积操作时需要拉普拉斯矩阵,而拉普拉斯矩阵需要知道整个图的结构,故无法完成inductive任务,而图注意力网络仅需要一阶邻居节点的信息。(transductive指的是训练、测试使用同一个图数据,inductive是指训练、测试使用不同的图数据)
- 图卷积神经网络对于同一个节点的不同邻居在卷积操作时使用的是相同的权重 W W W(详见图卷积神经网络最终使用的卷积公式),而图注意力网络则可以通过注意力机制针对不同的邻居学习不同的权重。
注意力机制是什么?
DNN中的注意力机制受到人处理信息的启发。由于信息处理能力有限,人会选择性地关注完整信息的一部分,忽略其他信息。
注意力机制的核心在于对给定信息进行权重分配,权重高的信息意味着需要系统进行重点加工。
下面阐述神经网络中注意力机制的数学表达形式,Attention函数的本质可以被描述为一个查询(query)到一系列(键key-值value)对的映射。

其中,Source是需要系统处理的信息源,Query代表某种条件或者先验信息,Attention Value是给定Query信息的条件下,通过注意力机制从Source中提取得到的信息。一般Source里面包含多种信息,将每种信息通过Key-Value对的形式表示出来。注意力机制的定义如下:
A t t e n t i o n ( Q u e r y , S o u r c e ) = ∑ i s i m i l a r i t y ( Q u e r y , K e y i ) ⋅ V a l u e i Attention(Query, Source)=\sum_i similarity(Query, Key_i)\cdot Value_i Attention(Query,Source)=i∑similarity(Query,Keyi)⋅Valuei
上式中Query,Key,Value,Attention Value在实际计算时均可以是向量形式。 s i m i l a r i t y ( Q u e r y , K e y i ) similarity(Query, Key_i) similarity(Query,Keyi)表示Query向量和Key向量的相关度,最直接的方法是可以取两向量的内积 < Q u e r y , K e y i >
上式表明注意力机制就是对所有的Value信息进行加权求和,权重是Query与对应Key的相关度。
图注意力层(Graph Attentional Layer)
根据注意力机制里面的三要素:Query, Source, Attention Value,可以将Query设置为当前中心节点的特征向量,将Source设置为所有邻居的特征向量,将Attention Value设置为中心节点经过聚合操作后的新的特征向量。
对于一个 N N N节点的图,我们一共会构造 N N N个图注意力网络,因为每一个节点都需要对于其邻域节点训练相应的注意力。而图注意力网络的层数 K K K则根据需要决定。我们在这里先分析 K = 1 K=1 K=1,即一个单层图注意力网络的工作原理。
设图中任意节点 v i v_i vi在第 l l l层所对应的特征向量为 h i , h i ∈ R d ( l ) h_i,h_i\in R^{d^{(l)}} hi,hi∈Rd(l), d ( l ) d^{(l)} d(l)表示节点的特征长度,经过一个以注意力机制为核心的聚合操作之后,输出的是每个节点新的特征向量 h i ′ , h i ′ ∈ R d ( l + 1 ) h'_i,h'_i\in R^{d^{(l+1)}} hi′,hi′∈Rd(l+1), d l + 1 d^{l+1} dl+1表示输出的特征向量的长度。将这个聚合操作成为图注意力层(Graph Attention Layer, GAL)。
单层图注意力网络的输入为一个向量集 h = { h 1 ⃗ , h 2 ⃗ , . . . , h N ⃗ } , h i ⃗ ∈ R F h=\{\vec{h_1},\vec{h_2},...,\vec{h_N}\}, \vec{h_i}\in R^F h={h1,h2,...,hN},hi∈RF,输出为一个向量集 h ′ = { h 1 ′ ⃗ , h 2 ′ ⃗ , . . . , h N ′ ⃗ } , h i ′ ⃗ ∈ R F ′ h'=\{\vec{h'_1},\vec{h'_2},...,\vec{h'_N}\}, \vec{h'_i}\in R^{F'} h′={h1′,h2′,...,hN′},hi′∈RF′。即通过图注意力层后,原本的节点信息 h i ⃗ \vec{h_i} hi被更新为 h i ′ ⃗ \vec{h'_i} hi′。为了使得网络能够从原始输入中提取更深层次的信息,通常设 F ′ > F F'>F F′>F,即图注意力层是一个将信号升维的网络。
下图为节点 v i v_i vi的单层图注意力网络的其中一个邻居节点 v j v_j vj的结构表示:

对于节点 v i v_i vi,考虑其邻居节点 v j v_j vj到 v i v_i vi的注意力权重的计算过程。输入为两个向量 h i ⃗ , h j ⃗ ∈ R F \vec{h_i}, \vec{h_j}\in R^F hi,hj∈RF,为了将它们变换到 R F ′ R^{F'} RF′,引入一个待学习的权重矩阵 W ∈ R F ′ × F W\in R^{F'\times F} W∈RF′×F,以及一个待学习的向量 a ⃗ ∈ R 2 F ′ \vec{a}\in R^{2F'} a∈R2F′。
- 做两个运算: W ∗ h i ⃗ W*\vec{h_i} W∗hi和 W ∗ h j ⃗ W* \vec{h_j} W∗hj,得到两个 R F ′ R^{F'} RF′维向量
- 计算节点 v i v_i vi在节点 v j v_j vj上的注意力值 e i j = a ( W h i ⃗ , W h j ⃗ ) e_{ij}=a (W\vec{h_i},W\vec{h_j}) eij=a(Whi,Whj),也就是邻居节点 v j v_j vj到 v i v_i vi的权重系数,其中 W ∈ R d ( l + 1 ) × d ( l ) W\in R^{d^{(l+1)}\times d^{(l)}} W∈Rd(l+1)×d(l)是该层节点特征变换的权重参数。 a ( ⋅ ) a(\cdot) a(⋅)是计算两个节点相关度的函数,原则上可以计算图中任意一个节点到节点 v i v_i vi的权重系数,为了简化计算,将其限制在一阶邻居内,需要注意的是在GAT中,作者将每个节点也视为自己的邻居。
- 最后对于节点 v i v_i vi的所有邻居节点求得 e e e后,利用softmax完成注意力权重的归一化操作。
关于 a a a的选择,可以用向量的内积来定义一种无参形式的相关度计算 < W h i ⃗ , W h j ⃗ >
e i j = L e a k y R e L U ( a [ W h i ⃗ ∣ ∣ W h j ⃗ ] ) e_{ij}=LeakyReLU(a [W\vec{h_i}||W\vec{h_j}]) eij=LeakyReLU(a[Whi∣∣Whj])
其权重参数 a ∈ R 2 d ( l + 1 ) a\in R^{2d^{(l+1)}} a∈R2d(l+1),激活函数为LeakyReLU。另外,为了更好分配权重,需要将与所有邻居计算出的相关度进行统一的归一化处理,具体形式为softmax归一化:
α i j = s o f t m a x j ( e i j ) = exp e i j ∑ v k ∈ N ~ ( v i ) e x p ( e i k ) \alpha_{ij}=softmax_j(e_{ij})=\frac{\exp{e_{ij}}}{\sum_{v_k\in \tilde N(v_i)}exp(e_{ik})} αij=softmaxj(eij)=∑vk∈N~(vi)exp(eik)expeij
α \alpha α是权重系数,通过上式的处理,保证所有邻居的权重系数加和为1。
完整的权重系数的计算公式为:
α i j = exp ( L e a k y R e L U ( a ⃗ T [ W h i ⃗ ∣ ∣ W h j ⃗ ] ) ) ∑ v k ∈ N ( v i ) ~ exp ( L e a k y R e L U ( a ⃗ T [ W h i ⃗ ∣ ∣ W h j ⃗ ] ) ) \alpha_{ij}=\frac{\exp{(LeakyReLU(\vec{a}^T[W\vec{h_i}||W\vec{h_j}])})}{\sum_{v_k\in \tilde{N(v_i)}}{\exp{(LeakyReLU(\vec{a}^T[W\vec{h_i}||W\vec{h_j}]))}}} αij=∑vk∈N(vi)~exp(LeakyReLU(aT[Whi∣∣Whj]))exp(LeakyReLU(aT[Whi∣∣Whj]))
在归一化所有节点的注意力权重后,就可以通过图注意力层进行节点的信息提取了。整个网络的输出值 h i ′ ⃗ \vec{h'_i} hi′计算公式如下(其中 σ \sigma σ表示激活函数):
h i ′ ⃗ = σ ( ∑ v j ∈ N ~ ( v i ) α i j W h j ⃗ ) \vec{h'_i}=\sigma{(\sum_{v_j\in \tilde N(v_i)}\alpha_{ij}W\vec{h_j}}) hi′=σ(vj∈N~(vi)∑αijWhj)
多头图注意力层
为了进一步提升注意力层的表达能力,可以加入多头注意力机制(multi-head attention),即对上式调用K组相互独立的注意力机制,然后将输出结果拼接在一起:
h i ′ ⃗ = ∣ ∣ k = 1 K σ ( ∑ v j ∈ N ~ ( v i ) α i j ( k ) W ( k ) h j ⃗ ) \vec{h'_i}=||_{k=1}^K \sigma{(\sum_{v_j\in \tilde N(v_i)}\alpha_{ij}^{(k)}W^{(k)}\vec{h_j}}) hi′=∣∣k=1Kσ(vj∈N~(vi)∑αij(k)W(k)hj)
其中, ∣ ∣ || ∣∣表示拼接操作, α i j ( k ) \alpha_{ij}^{(k)} αij(k)是第 k k k组注意力机制计算出的权重系数, W ( k ) W^{(k)} W(k)是对应的学习参数。当然,为了减少输出的特征向量的维度,可以将拼接操作替换成平均操作。
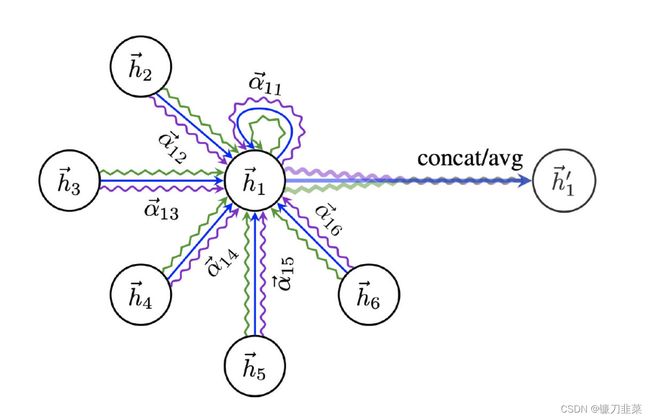
增加多组相互独立的注意力机制,使得多头注意力机制能够将注意力的分配放到中心节点与邻居节点之间多处相关的特征上,可使得系统的学习能力更加强大。
上图为一个三层图注意力网络(K=3),不同的颜色表示不同注意力计算过程,计算完成后,将上述结果进行拼接或者平均操作。多层注意力机制存在的意义在于:不同的特征可能需要分配不同的注意力权重,如果仅仅用单层注意力层,则对于该邻域节点的所有属性都采用了相同的注意力权重,这样将会减弱模型的学习能力。
图注意力层比GCN里面的图卷积层多了一个自适应的边权重系数的维度。回到GCN的核心过程 L ~ S Y M X W \tilde L_{SYM}XW L~SYMXW,可以将 L ~ s y m \tilde L_{sym} L~sym分拆成两个部分,引入一个权重矩阵 M ∈ R N × N M\in R^{N\times N} M∈RN×N,然后核心过程就变成了 ( A ~ ⊙ M ) X W (\tilde A \odot M)XW (A~⊙M)XW。由此看出,图注意力模型比GCN多了一个可以学习的新维度——边上的权重系数。
在之前的模型中,这个权重系数矩阵是图的拉普拉斯矩阵,而图注意力模型可以对其进行自适应的学习,并且通过运用注意力机制,避免引入过多的学习参数。这使得图注意力模型具有高效的表达能力。从图信号处理角度看,这种机制相当于学习出一个自适应的图位移算子,对应一种自适应的滤波效应。同时和GraphSAGE模型一样,图注意力模型的计算也保留了非常完整的局部性,一样可以进行归纳学习。
注意,特殊情况,如果我们将多层注意力网络应用到最后一层(输出层),应该将公式改为
h i ′ ⃗ = σ ( 1 K ∑ k = 1 K ∑ v j ∈ N ~ ( v i ) α i j k W k h j ⃗ ) \vec{h'_i}=\sigma{(\frac{1}{K} \sum_{k=1}^K \sum_{v_j\in \tilde N(v_i)}\alpha_{ij}^{k}W^{k}\vec{h_j}}) hi′=σ(K1k=1∑Kvj∈N~(vi)∑αijkWkhj)
从GNN到GCN再到GAT
- GNN:权重依靠人为设定或学习得到
- GCN:依赖于图结构决定更新权重。 H ( l + 1 ) = σ ( D ^ − 1 / 2 A ^ D ^ − 1 / 2 H ( l ) W ( l ) ) H^{(l+1)}=\sigma(\hat{D}^{−1/2}\hat{A}\hat{D}^{−1/2}H^{(l)}W^{(l)}) H(l+1)=σ(D^−1/2A^D^−1/2H(l)W(l))
- GAT:GAT是对于GCN在邻居权重分配问题上的改进。注意力通过Multi-head Attention 进行学习,相比于GCN的更新权重纯粹依赖于图结构更具有合理性。
参考资料
[1] 《深入浅出图神经网络:GNN原理解析》
[2] attention各种形式总结
[3] 图注意力网络-Graph Attention Network (GAT)
[4] 深度学习之注意力机制(Attention Mechanism)和Seq2Seq
[5] 图注意力网络GAT(含代码)