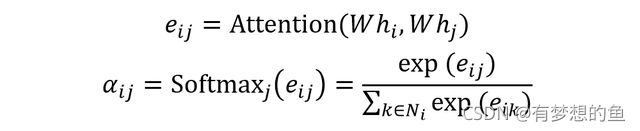GNN、GCN、GAT关系

图神经网络 Graph Neural Network (GNN)

参考文献：图神经网络 Graph Neural Network (GNN)

最早期的图神经网络 Graph Neural Network，简称 GNN。GNN 2009 年已经出现了，发表在论文《The graph neural network model》中。

下图展示了graph_focused 和 node_focused 的应用。图 (a) 为化学分子结构，需要预测分子结构对人体是否有害，则使用 graph_focused 的方法判断整个分子结构是否有害，而不用判断具体某个原子的有害性。图 (b) 是一个城堡图片，判断图中每一个节点是否属于城堡内部 (即黑点)，此时需要得到每一个节点的特征，并预测节点的类别，属于 node_focused。图 (c) 是网页连接结构，可以通过 node_focused 判断每一个网页的类型。

在图结构中，一个节点可以表示一个对象或概念，而边可以表示节点之间的关系。GNN 用一个状态向量 xn 表示节点 n 的状态，节点 n 的状态需要用四个部分的向量进行计算：节点 n 的特征向量、邻居节点的特征向量、邻居节点的状态向量、边 (与 n 相连) 的特征向量。如下图所示：

 

GNN 计算的公式主要包括传播和输出两个部分。传播部分主要是用 transition function f将邻居节点和边的信息结合在一起，得到当前节点的状态向量。输出部分用 output function o 将节点的特征和状态向量转为输出向量。transition function 和 output function 如下面的公式：

 

 

对于 positional graph，在使用 transition function 时，需要把邻居节点的位置信息也包含进来。例如可以将邻居节点的特征 l_ne[n]、状态 x_ne[n] 和边的特征 l_co[n] 按照 position 的顺序排列，然后还需要进行 pad，把不存在的邻居节点的位置置为空值。

对于 nonpositional graph，可以将 transition function 改成下面的形式，即对于所有邻居采用相同的方式处理，最后再相加。

 图卷积网络 GCN 是 2016 年被提出的。

参考文献38.图神经网络 GNN 之图卷积网络 (GCN)

传统的神经网络比较适合用于欧式空间的数据，而图神经网络 GNN 可以把神经网络用在图结构 (Graph) 中。图神经网络的种类很多，包括图卷积网络 GCN、图注意力网络 GAT、图自编码器 GAE 等。

图卷积神经网络网络 Graph Convolutional Network (GCN) 最早是在 2016 年提出，2017 年发表在 ICLR 上。GCN 主要是将卷积操作应用到图结构上，如下图所示，GCN 输入的 chanel 为 C (即节点 Xi 特征向量的维度)，GCN 输出的 chanel 为 F，即每个节点 (Zi) 的特征向量维度为 F，最后用节点的特征对节点进行分类预测等：

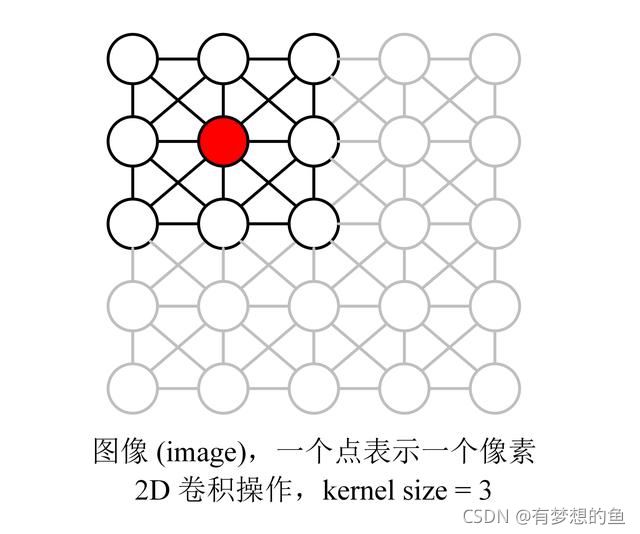
 GCN 和 CNN 类似，具有强大的特征学习能力，它们的实质也是类似的，某个点的卷积可以看成对该点邻居的加权求和。下图为传统的图像 (image) 卷积操作，每个点表示一个像素，图像的像素也可以看成是一种图 (graph) 结构，相邻的像素之间有边连接，而卷积是对像素邻居进行加权平均得到的。

 而对于图 (graph) 结构，也可以采取类似的方法进行卷积。例如对下图中红色的节点卷积就等于取其邻居节点进行加权平均。

 

GCN 中给出了图卷积的计算公式，如下所示，其中 H(l) 表示节点在第 l 层的特征向量，H(l+1) 表示经过卷积后节点在第 l+1 层的特征向量，W(l) 表示第 l 层卷积的参数，σ 表示激活函数。而由矩阵 A、D组成的部分是一种拉普拉斯矩阵 (Laplacian matrix)，

 

A+I 中的 I 为单位矩阵，即对角线为 1，其他为 0 的矩阵：

 上面的公式就是就是 GCN 卷积操作的公式了，通过多层 GCN 卷积，就可以提取出每个节点需要的信息，用于各种分类或分析。

 GAT 图注意力网络 Graph Attention Network

GCN 缺点

在之前的文章38.图神经网络 GNN 之图卷积网络 (GCN)介绍了图卷积神经网络 GCN，不熟悉的童鞋可以参考一下。GNN 模型可以分为频谱域 (spectral domain) 和空间域 (spatial domain) 两大类：spectral 的方法通常利用了拉普拉斯矩阵，借助图谱的方式进行卷积操作；spatial 的方法通常使用更直接的方式聚合邻居节点的信息。

之前介绍的该 GCN 模型是基于频谱域 (spectral domain) 的，利用了拉普拉斯矩阵，总的来说 GCN 存在下面的缺点：

GCN 假设图是无向的，因为利用了对称的拉普拉斯矩阵 (只有邻接矩阵 A 是对称的，拉普拉斯矩阵才可以正交分解)，不能直接用于有向图。GCN 的作者为了处理有向图，需要对 Graph 结构进行调整，要把有向边划分成两个节点放入 Graph 中。例如 e1、e2 为两个节点，r 为 e1，e2 的有向关系，则需要把 r 划分为两个关系节点 r1 和 r2 放入图中。连接 (e1, r1)、(e2, r2)。

GCN 不能处理动态图，GCN 在训练时依赖于具体的图结构，测试的时候也要在相同的图上进行。因此只能处理 transductive 任务，不能处理 inductive 任务。transductive 指训练和测试的时候基于相同的图结构，例如在一个社交网络上，知道一部分人的类别，预测另一部分人的类别。inductive 指训练和测试使用不同的图结构，例如在一个社交网络上训练，在另一个社交网络上预测。

GCN 不能为每个邻居分配不同的权重，GCN 在卷积时对所有邻居节点均一视同仁，不能根据节点重要性分配不同的权重。

2018 年图注意力网络 GAT 被提出，用于解决 GCN 的上述问题，论文是《GRAPH ATTENTION NETWORKS》。GAT 采用了 Attention 机制，可以为不同节点分配不同权重，训练时依赖于成对的相邻节点，而不依赖具体的网络结构，可以用于 inductive 任务。

GAT

假设 Graph 包含 N 个节点，每个节点的特征向量为 hi，维度是 F，如下所示：

 对节点特征向量 h 进行线性变换，可以得到新的特征向量 h'i，维度是 F'，如下所示，W 为线性变换的矩阵：

 节点 j 是节点 i 的邻居，则可以使用 Attention 机制计算节点 j 对于节点 i 的重要性，即 Attention Score：

GAT 具体的 Attention 做法如下，把节点 i、j 的特征向量 h'i、h'j 拼接在一起，然后和一个 2F' 维的向量 a 计算内积。激活函数采用 LeakyReLU，公式如下：

 Attention 如下图所示：

 经过 Attention 之后节点 i 的特征向量如下：

 GAT 也可以采用 Multi-Head Attention，即多个 Attention，如下图所示：

 

 如果有 K 个 Attention，则需要把 K 个 Attention 生成的向量拼接在一起，如下：

 但是如果是最后一层，则 K 个 Attention 的输出不进行拼接，而是求平均。

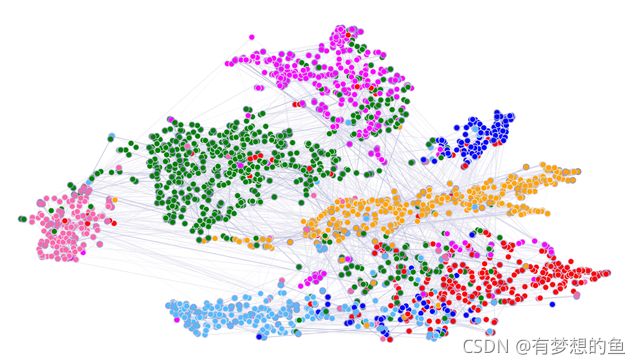
 取出节点在 GAT 第一层隐藏层向量，用 T-SNE 算法进行降维可视化，得到的结果如下，可以看到不同类别的节点可以比较好的区分。

GAT 总结

GAT 的时间复杂度为 O(|V|FF'+|E|F')，其中 |V|FF' 是计算所有节点特征向量变换的时间复杂度 (即 Wh)，|E|F' 是计算 Attention 的时间复杂度。GAT 不依赖于完整的图结构，只依赖于边，因此可以用于 inductive 任务。GAT 可用于有向图。采用 Attention 机制，可以为不同的邻居节点分配不同的权重。