迁移学习——Low-Rank Transfer Subspace Learning

《Low-Rank Transfer Subspace Learning》论文学习
2012 IEEE 12th International Conference on Data Mining

---

摘要

迁移学习的目的是通过处理源领域和目标领域之间的细微差异，找到将学习到的知识从源领域转移到目标领域的方法。
在本文中，我们提出了一种新的框架，通过低秩表示约束来解决上述知识转移问题。
在Yale B、CMU PIE、UBKinFace数据库上的大量实验验证了所提出方法的有效性。
Keywords-low-rank; transfer learning; domain adaptation;

---

一、介绍

低秩转移子空间学习(LTSL)

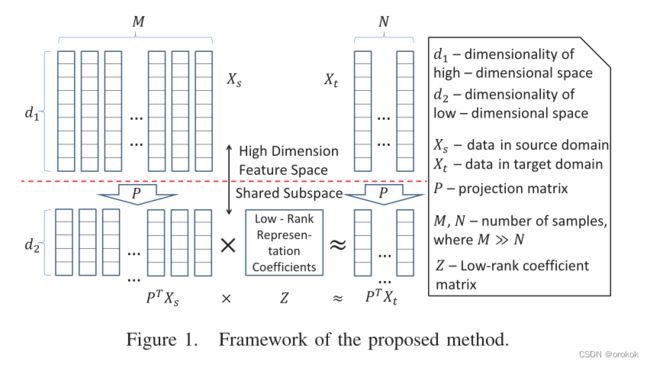
其核心思想是找到一个由投影矩阵$P$跨越的空间，其中目标域中的每个数据点与源域中的数据共享一个子空间，就好像这个单个数据点是严格从源域中的子空间绘制的一样。
我们的方法中存在两个任务，即寻找投影$P$和寻找源域和目标域中数据之间的映射。
第一个任务通过使用子空间学习方法
第二个任务通过低秩表示完成，该表示揭示了源域和目标域的子空间划分信息。

1.1相关工作

对迁移学习进行分类的一种常见方法是基于域和任务的属性。我们的框架属于转导迁移学习范畴。
低秩恢复（鲁棒PCA）、矩阵完成和低秩表示（LRR）是通过低秩约束计算损坏或缺失数据的鲁棒表示的方法。
此外，LRR同时恢复数据矩阵和结构信息，通过这些信息可以精确分割数据所在的子空间。
Si等人提出了一种基于子空间的转移学习，以减少源域和目标域之间的分布差异，这与本文提出的框架类似。但在以下方面存在一些差异：

1. 我们使用LRR代替分布散度来指导子空间学习
2. LRR对噪声、严重损坏以及异常值更具鲁棒性
3. 采用传统的转导学习方式，需要目标域中所有未标记的数据来更好地估计布雷格曼散度（为了统计充分性）。幸运的是，我们只需要目标域中的少量标记数据。

二、低秩转移子空间学习

2.1问题公式化

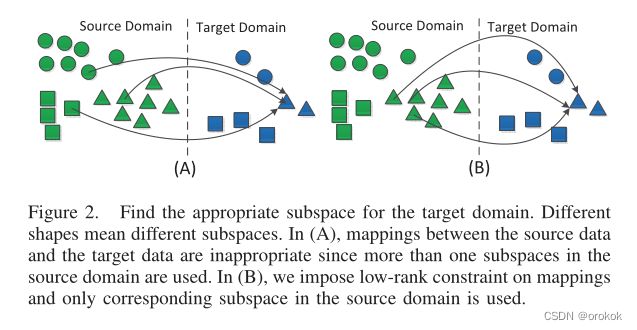
给定的数据集很少由单个子空间很好地描述，相反，数据更可能位于多个子空间中，为每个基准寻找合适的子空间形成了一个有趣的问题，称为子空间分割。正确的方法可能是仅使用适当子空间内源域中的少量数据来重建特定目标数据，如图2所示。

我们使用$X_t$、$X_s$表示来自目标域的测试数据，使用字典表示来自源域，使用$Z$指定$X_s$和$X_t$之间的线性关系。
我们感兴趣的是找到一个子空间$P$，其中来自目标域的测试数据可以由来自子空间并集的一些子空间$S_i$线性表示，其中$S_i$来自源域的子空间集${\bigcup }_{i=1}^k{S}_i$。
$P$和$S_i$的子空间的含义略有不同，前者本质上是一个投影，而后者是一组位于$P$中的数据。
基本问题： 目标是找到一个判别子空间P，其中测试数据可以由源域中具有秩约束的某个子空间$S_i$的数据线性表示。即：
$$\begin{array}{c}P,Z=\underset{P,Z}{argmin}F\left(P,X_s\right)+rank(Z),\\ s.t.,P^T{X}_t=P^T{X}_{s}Z,\end{array}\text{\hspace{1em}(1)}$$
其中$F(P,X_s)$是一般子空间学习函数，$rank(Z)$是投影子空间$P$中从$X_s$到$X_t$的知识转移的约束。
与LRR类似，我们也使用低秩约束系数矩阵$Z$，但在学习子空间$P$中平滑转移学习。

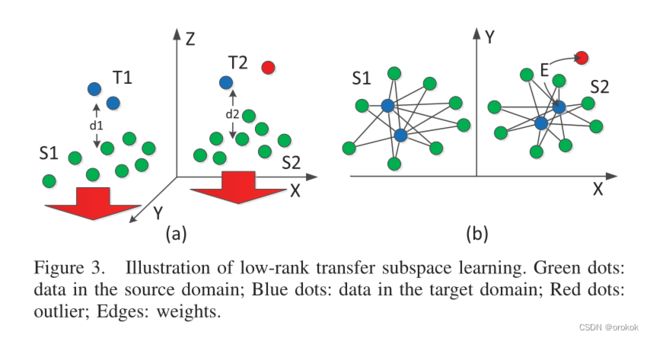
在右图中，所有数据都投影到二维空间，其中目标域中的大多数数据由源域中除红色外的一些子空间适当表示。这种行为可以用以下问题中的误差项E很好地解释：
$$\begin{array}{c}P,Z,E=\underset{P,Z,E}{argmin}F\left(P,X_s\right)+rank(Z)+\lambda \Vert E{\Vert }_{2,1},\\ s.t.,P^T{X}_t=P^T{X}_{s}Z+E,\end{array}\text{\hspace{1em}(2)}$$
我们使用的$l_{2,1}$范数表示图3中所示的样本特定误差。
$T2$的红色数据不能正确地由$S2$中的源数据表示，因为其间有较大的间距E。添加一个项$E$可以解释这种情况，我们仍然可以通过消除该误差找到该“异常值”（$S2$中对应的蓝点）b的表示。
核规范$\Vert \cdot {\Vert }_{\ast }$是秩最小化问题的良好替代，我们将问题重写为：
$$\begin{array}{c}P,Z,E=\underset{P,Z,E}{argmin}F\left(P,X_s\right)+\Vert Z{\Vert }_{\ast }+\lambda \Vert E{\Vert }_{2,1},\\ s.t.,P^T{X}_t=P^T{X}_{s}Z+E,\end{array}\text{\hspace{1em}(3)}$$
通过求解$P$和$Z$，我们可以为目标域中的每个数据$x_t$找到合适的子空间$S_i$和系数向量。
我们在目标数据上使用子空间学习函数的能量，即$F(P,X_t)$，来衡量子空间$P$的有效性。根据这个测量，下一个定理揭示了$F(P,X_t)$在温和条件下是$F(P,X_s)$加上一个小项的下界。
给定$P,Z$通过问题(1)和对应的子空间学习能量函数$F(P,S_i)$和$F(P,T_i)$学习，其中$S_i$是源域的某子空间。$T_i$是目标域的某子空间，可以通过系数矩阵$Z_i$用$S_i$线性表示。设$|S_i|=|T_i|$，即$Z_i$是一个方阵。则$F(P,T_i)$的界限为:
$$F(P,T_i)\ge F(P,S_i)\Vert \widehat{Z_i^{-1}}{\Vert }_F^{-2}+\xi ,\text{\hspace{1em}(4)}$$
其中$\widehat{Z_i}=Z_i+\gamma \mathbf{I}$是一个可逆矩阵，$\gamma \mathbf{I}$是一个小扰动项，以确保$\widehat{Z_i}$是非奇异的，$\xi =F(P,T_i)-F(P,\widehat{T_i})$。$\widehat{T_i}$表示被$\widehat{Z_i}\Vert \cdot {\Vert }_F$扰动的目标域数据，表示矩阵Frobenius范数。

2.2求解优化问题

我们将问题(3)转化为以下等价问题:
$$\begin{gathered} \underset{Z,E,J,P}{argmin}F(P,X_s)+\Vert J{\Vert }_{\ast }+\lambda \Vert E{\Vert }_{2,1}, \\ s.t.,P^T{X}_t=P^T{X}_{s}Z+E,Z=J.\text{\hspace{1em}(5)} \end{gathered}$$
如果$F(P,X_s)$是凸的，那么我们通过最小化以下增广拉格朗日乘子$(ALM)$函数$L$来解决上述问题:
$$\begin{gathered} \mathcal{L}=F(P,X_s)+\Vert J{\Vert }_{\ast }+\lambda \Vert E{\Vert }_{2,1} \\ +<Y_1,P^T{X}_t-P^T{X}_{s}Z-E>+<Y_2,Z-J> \\ +\frac{\mu }{2}(\Vert P^T{X}_t-P^T{X}_{s}Z-E{\Vert }_F^2+\Vert Z-J{\Vert }_F^2),\text{\hspace{1em}(6)} \end{gathered}$$
式中$Y_1、Y_2$为拉格朗日乘子，$\mu >0$为惩罚参数。
我们采用不精确ALM来解决上述问题，其时间效率和有效性在算法1中概述。

2.3计算复杂度

为简单起见，我们假设$X_s$和$X_t$都属于$m\times n$矩阵。算法1中最耗时的部分是步骤(1)中$n\times n$矩阵的SVD计算。当样本数量$n$较大时，其计算代价变得非常高，即$O(n^3)$。
[22]中的定理4.3为解决步骤(1)中的问题提供了更好的方法，问题(5)中一次迭代的时间代价为$O(mnr+n{r}^2+r^3)$，其中$r$为源数据$X_s$的秩。考虑正交过程和迭代过程，上述问题的计算复杂度总和为$O(m^{2}n)+O(N(mnr+n{r}^2+r^3))$，其中$N$为迭代次数。

三、LTSL实例

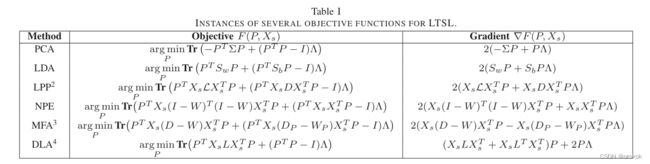
在本节中，我们展示了如何将低秩转移子空间学习应用于传统的子空间学习方法:$PCA[31]、LDA[2]、LPP[16]、MFA[33]、NPE[15]、DLA[35]$。由算法1可知，这些方法的区别在于:$\nabla F(P,X_s)$。
例如，PCA的目标函数为:
$$\underset{P^{T}P=I}{\min }F(P,X_s)=\underset{P^{T}P=I}{\min }\mathbf{T}\mathbf{r}(-P^T\Sigma P),\text{\hspace{1em}(7)}$$
其中$\Sigma$为数据协方差矩阵。通过拉格朗日乘子法，将问题(7)改写为:
$$\underset{P}{\min }\mathbf{T}\mathbf{r}(-P^T\Sigma P+(P^{T}P-I)\Lambda ),$$
其中$\Lambda$为拉格朗日乘子，对应的$PCA$梯度为$\nabla F(P,X_s)=2(-\Sigma P+P\Lambda )$。在表一中，我们展示了各种各样的方法的目标函数和$F(P,X_s)$ 对$P$的导数。

四、实验评价

在本节中，我们将我们的方法，例如，$LT-PCA,LT-LDA,LT-LPP,LT-MFA,LT-NPE和LT-DLA$与传统的子空间算法，例如$PCA[31]，LDA[2]，LPP[16]，MFA[33]，NPE[15]，DLA[35]，$转移子空间学习(TSL)[30]，以及耶鲁B, CMU PIE和UB kinface中的令人沮丧的简单域适应(FEDA)[10]进行比较。除FEDA采用SVM作为分类器外，其他基于子空间学习的方法均采用最近邻(nearest-neighbor, NN)作为分类器。

4.1合成数据的实验

如图4(左)所示，源域中有两类数据，目标域中有两类数据。所有数据都在三维空间中，由不同均值和协方差矩阵的高斯分布产生。源域的每个类都是密集的，有100个样本，而目标域的每个类都是稀疏的，有30个样本。显然，在源域很容易找到一个超平面来分割样本。然而，在目标域中，决策边界似乎并不明确。

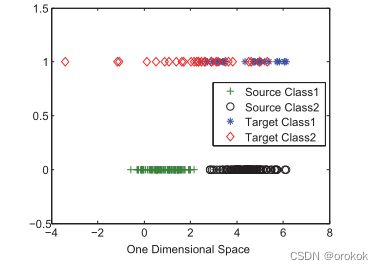
在图4(中)中，我们通过提出的方法找到了一个合适的子空间，即一个一维空间，目标中的每个数据都由源域中某个类的数据线性表示。在这个空间中，由于源域中的数据是分离良好的，目标域中的数据也是可分离的，除了一些边界点。
在中间的图中，Y轴没有确切的含义，我们只是使用0和1来索引源数据和目标数据。

4.2 UB KinFace数据库

UB KinFace是第一个包含儿童及其父母在不同年龄的面部图像的数据库。目前的UB KinFace V er2.0包含400人的600张图片，可以分成200组。每个组由儿童、年轻父母和年老父母的图像组成。
亲属关系验证可以描述为:给定一对图像，确定图像中的人是否有亲属关系。本实验采用Gabor滤波器在8个方向、5个尺度上提取特征。
本实验采用五次交叉验证，即160张年轻父母和孩子的图像特征为源数据$X_s$, 160张年老父母和孩子的图像特征为目标数据$X_t$。
注意，我们使用特征在子女和父母之间的差异的绝对值作为亲属关系验证的输入。同一家庭两个人的差异为正样本，不同家庭两个人的差异为负样本。
当然，负样本可能比正样本多得多，在我们的配置中，我们将它们设置为160:640。其余40张老年人和儿童图像作为测试样本，正样本与负样本之比为40:40。
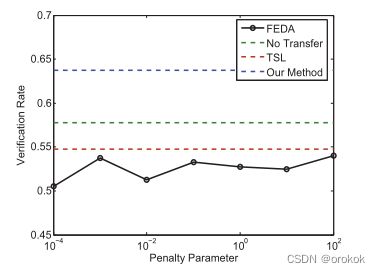
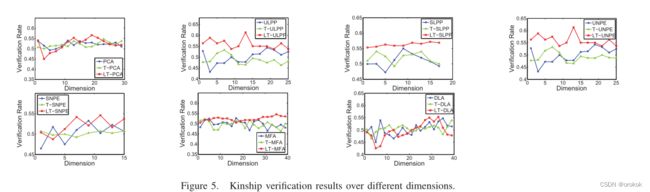
实验结果如表II、图4(右)、图5所示。

4.3 Yale B and CMU PIE数据库

Yale B数据库包含38个受试者的面部图像，每个受试者有64张不同光照下的图像。
CMU PIE包括68个个体，在关闭环境灯的情况下，每个个体处于21种不同的照明条件下。
在我们的实验中，只考虑正面的面部图像。我们将图像裁剪成$30\times 30$的大小，只使用原始图像作为输入。
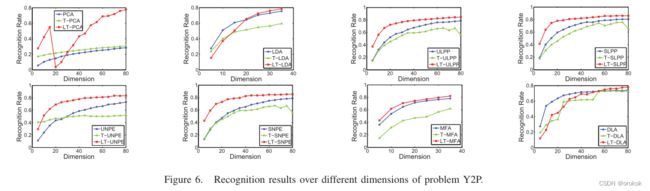
我们使用Yale B数据库作为源数据，CMU PIE作为目标数据，即Y2P。
注意，在图库中，每个主题只有正面自然光照的一面用作参考。
此外，这些图像是我们模型中的目标数据。
具体来说，在这个实验中，38个被试在Yale B的图片在我们的模型中都是$X_s$，而CMU PIE只有68张图片是$X_t$。
实验结果如表III、图6所示。

4.4讨论

选择每种方法的最佳性能，与FEDA在SVM中使用的不同惩罚参数“C”进行比较。
显然，所有基于子空间学习的方法都优于FEDA。
我们没有在Y2P上比较FEDA的原因是FEDA不能直接扩展到多类情况。
然而，我们的方法可以突破这一限制，并且在多类到多类的知识转移中也能很好地工作。

亲缘关系验证非常具有挑战性。
UB KinFace的图像来自现实世界，具有任意的变化，例如，姿势，照明，表情。
结果显示，即使是人类也不能很好地处理这个数据库，只能达到56.00%。
我们发现在设计的实验中，TSL方法的性能比传统方法差。原因是TSL对数据大小很敏感。
一方面，在目标域数据较少的情况下(我们只使用每个被试的一张图像作为图库)，无法通过核密度估计(KDE)方法准确描述其分布。
另一方面，即使有足够的数据，当规模较大时，TSL也很难收敛，
在这两种情况下，提出的低秩转移子空间学习仍然工作良好。

总结

在本文中，我们提出了一个新的迁移子空间学习框架。本质上，我们利用低秩约束在低维空间中架起源和目标域的桥梁。此外，许多成熟的方法可以纳入到我们的框架中，形成它们的低秩转移版本。
在Yale B、CMU PIE和UB KinFace数据库上的大量实验结果充分验证了我们的方法在解决跨数据库学习问题上的有效性。

References

1. 《Low-Rank Transfer Subspace Learning》论文学习
   2012 IEEE 12th International Conference on Data Mining