论文阅读笔记(18):Graph Convolutional Subspace Clustering,图卷积子空间聚类
论文阅读笔记(18):Graph Convolutional Subspace Clustering: A Robust Subspace Clustering Framework for Hyperspectral Image
- 摘要
- 简介
- 相关工作
-
- 子空间聚类
- 图卷积网络
- 方法论
-
- 图卷积子空间聚类(GCSC)
- 高效GCSC
- 高效核GCSC
- 使用GCSC对HSI聚类
摘要
高光谱(HSI)图像聚类是一项具有挑战性的任务。子空间聚类已被证明是利用数据点之间的内在关系的强大工具。在本文中,我们重新研究了图卷积子空间聚类,提出了一种新的子空间聚类框架,称为图卷积子空间聚类(GCSC),用于鲁棒HSI聚类。具体地说,该框架将数据的自表达特性重新构造到非欧几里德域中,从而生成一个更健壮的图嵌入字典。我们证明了传统的子空间聚类模型是欧几里德数据框架的特殊形式。在此框架的基础上,我们进一步利用Frobenius范数提出了两种新的子空间聚类模型,即高效GCSC(EGCSC)和高效核GCSC(EKGCSC)。这两个模型都有一个全局最优的闭式解,这使得它们更易于实现、训练和实际应用。
简介
为了避免人工数据标注,许多工作都致力于开发无监督的HSI分类方法,即HSI聚类。HSI聚类的目的不是使用标签信息,而是找到数据点之间的内在关系,并以无监督的方式自动确定标签[13]。HSI聚类的关键是测量数据点之间的相似性。传统的聚类方法,例如K-means,经常使用成对距离作为相似性度量,例如欧几里德距离。由于混合像素和冗余带问题,这些方法经常遭受不可靠的测量,并使HSI聚类面临巨大挑战。
以往的子空间聚类模型都是基于欧几里德数据的,往往忽略了数据点中固有的图结构。一方面,数据点通常被噪声破坏,或者可能有带有较大错误的条目。另一方面,尽管流形正则化有助于将图信息纳入子空间聚类,如图正则化LRSC,但它通常需要添加额外的正则化项和折衷参数。图神经网络(GNN)的最新发展将处理欧几里德数据的强大CNN推广到建模图结构数据。这使我们能够重新审视GNNs的传统问题。
为了同时学习图嵌入和affinity,本文提出了一种图卷积子空间聚类(GCSC)框架,将传统的子空间聚类方法重新构造为非欧几里德域。具体而言,GCSC框架通过利用结合了图形和特征信息的图卷积自表示模型来计算子空间聚类的自表示系数。从视觉上看,这进一步说明了将聚类模型与特征学习相结合的潜力。

图1。在图中,蓝色和红色点表示分别位于子空间S1和S2中的两个不同类。带有蓝色轮廓的红点和带有红色轮廓的蓝点表示错误分类的点。直观地说,GCSC将传统的数据转化为图结构数据,并采用图卷积生成鲁棒嵌入,用于后续的子空间聚类。
相关工作
子空间聚类
子空间聚类可以用如下自表示问题定义:
![]()
在稀疏子空间聚类(SSC)中,自表示问题变为:
![]()
此外,当 X = X W + N X=XW+N X=XW+N时,子空间聚类可以对任意噪音建模。
使用凸优化方法,如交替方向乘子法(ADMM),可以有效地解决上述问题。一旦找到系数矩阵W,子空间聚类将寻求通过谱聚类(SC)对亲和矩阵 A = 1 2 ( ∣ W ∣ + ∣ W ∣ T ) A=\frac{1}{2}(| W |+| W|^T) A=21(∣W∣+∣W∣T)进行分割。
图卷积网络
人们对将卷积推广到图域。最新的GNNs允许在图结构数据上有效地近似卷积。GNN通常可分为两类:谱卷积,通过使用图形傅里叶变换或其扩展将节点表示转换为谱域来执行卷积;空间卷积,通过考虑节点邻域来执行卷积。本文涉及的图卷积是谱卷积。
最具代表性的图卷积模型之一是Kift等人开发的图卷积网络(GCN)。GCN通过使用1阶切比雪夫多项式逼近光谱滤波器,并将归一化图拉普拉斯矩阵的最大特征值 L s y m L_{sym} Lsym设置为2。在形式上,GCN对图上的谱卷积定义如下:
![]()
这里, A ~ = I N + A \tilde A=I_N+A A~=IN+A是自循环的邻接矩阵,表示 D ~ \tilde D D~表示节点的度(degree)矩阵,其元素由 D ~ i i = ∑ j A ~ i j \tilde D_{ii}=\sum_j \tilde A_{ij} D~ii=∑jA~ij给出, W ∈ R m × l W∈\mathbb R^{m×l} W∈Rm×l表示一个可训练的参数矩阵,σ是一个非线性激活函数。具体地说,GCN将节点特征矩阵 X X X和邻接矩阵 A A A作为输入,并生成图嵌入 H ∈ R N × l H∈\mathbb R^{N×l} H∈RN×l,其中 l l l是输出维度。
GCN最初是为半监督节点分类而开发的。通过叠加多个图卷积层,GCN可以学习更深层次的图表示。与传统的深度神经网络类似,GCN可以很容易地使用梯度下降方法进行训练。在不同的任务中,GCN模型允许在非欧几里德域中修改许多传统问题。
方法论
图卷积子空间聚类(GCSC)
GCSC框架的目标是利用图卷积来学习一个健壮的affinity。为此,我们首先对传统的自表示问题进行如下修改:
![]()
其中 Z ∈ R N × N Z∈\mathbb R^{N×N} Z∈RN×N为自表示系数矩阵, A ‾ = D ~ − 1 / 2 A ~ D − 1 / 2 \overline A=\tilde D^{-1/2}\tilde AD^{-1/2} A=D~−1/2A~D−1/2为规范化后的对称自循环拉普拉斯矩阵。
注意, X A ‾ Z X\overline A Z XAZ可以被视为一个由 Z Z Z参数化的特殊线性图卷积运算(或特殊的图自动编码器),我们称为图卷积自表示。与传统的子空间聚类模型类似地,GCSC框架可以重写为:

很容易证明传统的子空间模型是我们框架的特例,因为传统的子空间模型只依赖于数据特征。式(6)可用传统子空间聚类中采用的相同方法有效求解。一旦获得了自表示系数矩阵 Z Z Z,就可以使用SC生成聚类结果。
高效GCSC
高效GCSC(EGCSC)对重构损失和系数矩阵都使用Frobenius范数:

Pan等人证明了即使没有对角约束 d i a g ( Z ) = 0 diag(Z)=0 diag(Z)=0,Frobenius范数也不会产生平凡解。这导致了稠密的自表示系数矩阵,可以表示为一个有效的闭式解。解如下:

获得Z后,我们可以使用它为SC构造亲和矩阵C。然而,文献中没有关于这一步骤的全局解。大多数现有工作通常通过 C = ∣ Z ∣ + ∣ Z ∣ T C=| Z |+| Z |^ T C=∣Z∣+∣Z∣T或 ∣ Z ∣ | Z | ∣Z∣计算亲和矩阵。在本文中,我们使用高效稠密子空间聚类(EDSC)所采用的启发式方法来增强块结构,这被证明有助于提高聚类精度。EGCSC在算法1中给出。

高效核GCSC
我们提出了EGCSC方法。然而,EGCSC模型本质上是在线性子空间上建模的。由于HSI的复杂性和非线性,大量研究表明非线性模型比线性模型具有更好的性能。在本小节中,我们使用核技巧提供了EGCSC的非线性扩展。该扩展称为高效内核GCSC(EKGCSC)。
令 Φ : R m ↦ H \Phi :\mathbb R^m\mapsto \mathcal H Φ:Rm↦H为从输入空间到可再生核希尔伯特空间 H \mathcal H H的一个映射。我们定义一个半正定核Gram矩阵 K X X ∈ R N × N {\bf K_{XX}}\in \mathbb R^{N\times N} KXX∈RN×N的元素:

其中 κ : R m × R m → \kappa:\mathbb R^m\times \mathbb R^m\rightarrow κ:Rm×Rm→为核函数。在这里我们使用带参数 γ \gamma γ的高斯核: κ ( x i , x j ) = e − γ ∥ x i − x j ∥ 2 \kappa(x_i,x_j)=e^{-\gamma\|x_i-x_j\|^2} κ(xi,xj)=e−γ∥xi−xj∥2。于是,高效核GCSC(EKGCSC)可以表示为:
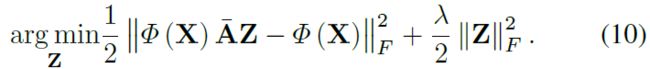
公式10的优化目标可以重写为:

上述问题可通过计算相对Z的偏导并令其为零来求解。EKGCSC的闭式解由下式给出:

EKGCSC模型将原始数据点显式映射到高维空间,从而使线性不可分问题成为可分问题。我们使用一种类似于EGCSC的方式构造亲和矩阵,并通过SC获得最终的聚类结果。算法2给出了EKGCSC的伪码。

使用GCSC对HSI聚类
。在使用GCSC模型之前,需要解决两个基本问题。
- HSI数据通常包含许多具有大量冗余的谱带,因此仅使用谱特征很难获得良好的性能。
- GCSC模型基于图结构数据,但HSI通常是欧几里德数据。
为解决第一个问题,采我们首先使用主成分分析(PCA)通过保留前d个主成分来降维。一方面,PCA减少了HSI数据中包含的冗余信息。另一方面,它提高了模型训练时的计算效率。为了同时考虑光谱和空间信息,我们通过提取三维面片来表示每个数据点。具体而言,每个数据点由中心像素及其相邻像素表示。该方法广泛应用于不同的HSI光谱空间分类方法。
对于第二个问题,我们构造一个k-最近邻(kNN)图来表示数据点的图结构。具体地说,每个数据点被看作是图上的节点,并且 x i x_i xi的k-最近邻由边缘关系组成。kNN图的邻接矩阵A定义如下:

其中 N k ( x i ) \mathcal N_k(x_i) Nk(xi)即为通过欧氏距离计算得到的k个 x i x_i xi最近邻。
从稀疏表示的角度来看,GCSC的目标是使用自表达字典矩阵 Y = X A ‾ Y=X\overline A Y=XA来重构原始数据。由于Y考虑了全局结构信息,因此可以消除这些噪声点并获得清晰的字典,这有利于生成鲁棒的亲和矩阵。从图3可以看出,结果Y显示出比原始X更好的聚类特性。可以从图表示学习的角度进一步解释。图卷积本质上是拉普拉斯平滑的一种特殊形式,它结合了节点及其相邻节点的特征。该操作使同一集群中的节点的特征相似,从而大大简化了集群任务。

图3。从印度松树数据集中选择的数据点的可视化,其中我们随机选择每类100个数据点,并使用t-SNE将其特征维数降低为2。(a) 原始数据点。(b) 使用图卷积进行嵌入。可以看出,它们通过图卷积变换后更紧凑。
GCSC模型与传统子空间模型的主要区别如下。首先,GCSC是在非欧几里德域中构建的。在GCSC框架下,传统的子空间聚类模型可以看作是欧氏域的特例。其次,GCSC通过图卷积将图结构合并,而传统的子空间聚类模型通过流形正则化来实现。因此,GCSC使用更直接的方式利用图形信息。


