读书笔记 | 自动驾驶中的雷达信号处理（第8章 雷达目标识别与分类技术）

本文编辑：调皮哥的小助理

大家好，我是调皮哥，又和大家见面了，时间过得很快，到目前为止，本次读书笔记的内容已经快接近尾声了，相信大家通过之前文章的阅读，已经掌握了雷达系统、雷达信号处理、雷达数据处理、雷达波形设计、雷达目标检测、数字信号处理等方面的基础内容和有关算法。

今天是《自动驾驶中的雷达处理算法》专栏的第9篇文章，我们继续来研究雷达数据处理之上的高级算法，我个人认为这个层面的算法是“雷达+人工智能算法”的架构，即采用深度学习、机器学习、神经网络等人工智能算法来分析、处理雷达输出的数据，包括结合激光雷达、计算机视觉等传感器形成多传感器融合处理的模式，主要用于自动驾驶、无人驾驶、辅助驾驶等领域。

8.1介绍

雷达目标识别技术逐渐成为了汽车雷达处理算法的重要组成部分，汽车雷达工作的环境是高度复杂的，提高道路行人识别能力的需求也越来越大，因此汽车雷达必须具备高精度区分感兴趣的目标（人、自行车、障碍物、其他车辆）的能力。

目标识别技术可以对被检测物体进行区分和分类，识别完成之后，就有可以针对特定类型的目标优化信号处理算法，例如，针对客车和行人可以采用不同的跟踪和滤波算法，这样可以提高雷达的检测效果，这种就有点类似于自适应动态调整。

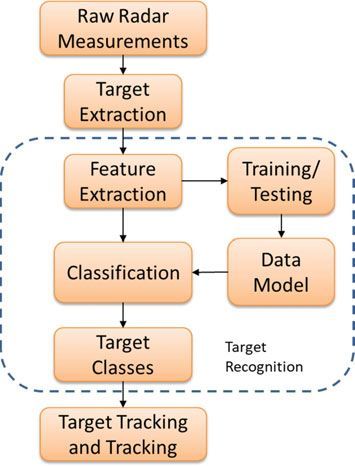
（图8.1涉及目标识别的雷达处理信号流程）

涉及目标识别的雷达处理一般流程如图8.1所示，目标识别技术采用各种各样的机器学习算法，机器学习有两大类:有监督机器学习（监督&半监督）和无监督机器学习。

（1）监督机器学习算法：使用标记标签的输入数据学习得到映射函数，当给定新的未标记数据时，映射函数会生成适当的输出。监督学习算法使用训练数据集的学习过程就是的“监督学习”过程，监督学习可以分为分类学习和回归学习，分类过程产生离散的或分类的输出，如汽车、自行车、行人或卡车；回归学习会产生实值输出，如高度或宽度。
（2）无监督机器学习算法：与监督学习相反，输入的训练数据没有标记标签。

在本文中，我们探索并总结了一些可以用于目标识别和分类的算法，主要是监督学习算法。本文的目的不是涵盖所有机器学习算法，而是为读者在进行汽车雷达处理时提供一些入门的思路，关于如何深入地学习目标识别算法，调皮哥建议阅读相关的文献，如图像处理、计算机视觉、统计等领域的内容。

另外，提醒各位读者，其实今天的这篇文章可以结合下面这篇综述《机器学习算法如何用于雷达信号分析与处理？》一同学习：

干货 | 机器学习算法如何用于雷达信号分析与处理？

8.2目标识别算法

8.2.1 KNN(K近邻)

K近邻(KNN)算法是一种非常成熟、简单且应用广泛的非参数监督机器学习算法，它可以应用于分类和回归两类问题。它使用距离度量，如欧几里得距离对给定数据进行分类，图8.2说明了KNN的概念。

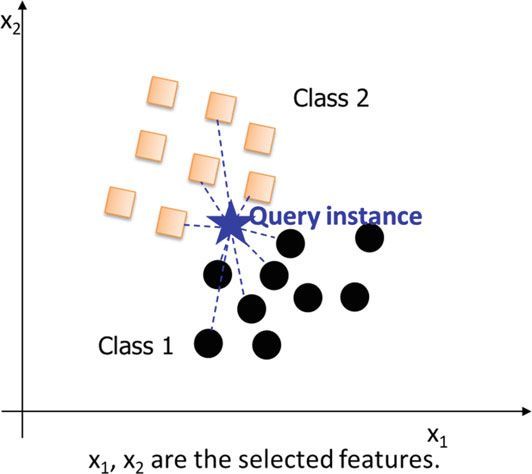
（图8.2 KNN概念的图解，显示了一些选定样本的距离计算）

对于分类，KNN可以通过以下简单步骤进行。

1.设置最近邻点的个数K。
2.计算被检测点（查询点）与所有训练样本数据的距离。
3. 按升序对距离进行排序，保留训练样本数据中的索引。
4. 从排序的距离中选择前 K 个条目。
5. 提取选中的 K 个条目的标签。
6. 计算 K 个标签的模式。

KNN算法的优点是简单，不需要对数据进行假设，具有较高的精度，可以用于分类和回归。然而，KNN的缺点是需要存储所有训练数据，在计算复杂性和对大型数据集的内存需求方面存在限制。而且KNN对噪声很敏感，这可能对汽车雷达数据构成挑战，下面我们给出一个简单的例子来说明KNN算法：

考虑一个二分类问题，两类数据分别以 $(x1,x2)=(2,3)$ 和 $(x1,x2)=(3,4)$为中心，并使用该数据作为训练数据。现在，我们希望对查询点$p1=(2.4,3.4)$ 和 $p2=(2.8,3.8)$进行分类，如图8.3所。其中，1类数据和2类数据分别用红色方框和黑色圆圈表示，而查询点用蓝色(星号)标记。通过KNN对这些查询点进行分类， $K=3$ 的结果如图8.4所示。

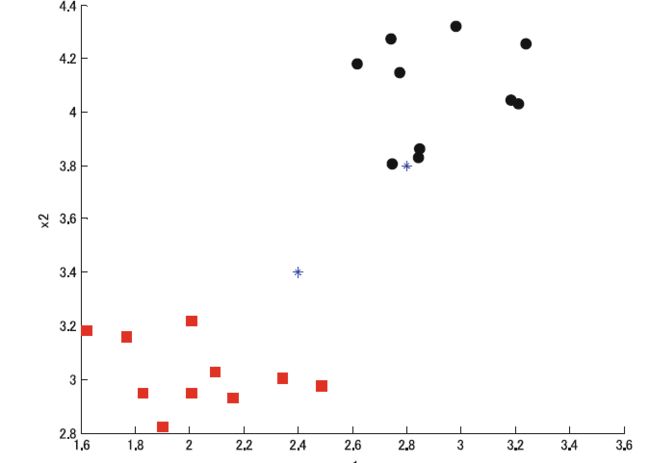
（图8.3本例中用于说明KNN分类的数据）

如图 8.4 所示，KNN 算法能够对查询数据进行正确分类，即下方的查询点为1类，上方的查询点为2类。但是如果类分离不充分时会出现问题，这可能引起错误分类。

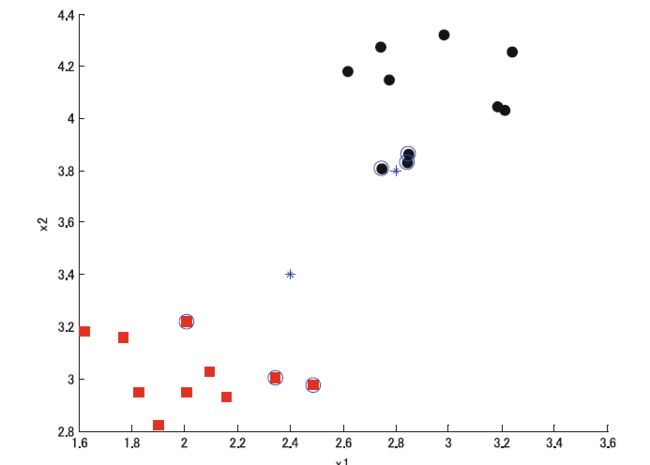
（图8.4 KNN分类结果）

8.2.2 线性判别分析(LDA)与二次判别分析(QDA)

一般情况下，有三类判别函数，对应的方法有三种:

（1）LDA基于线性判别函数，
（2）二次判别分析(QDA)基于二阶判别函数，
（3）非线性判别分析(NDA)基于非线性判别函数。

我们主要关注LDA和QDA，因为它们在实践中是常用的。

1. 线性判别分析

LDA是对目标进行分类的最简单、最著名的算法之一，最初由Fisher提出，因此在文献中也被称为Fisher的线性判别分析。如图8.5所示，LDA是一个线性分类器，基本工作原理是利用正交性从观测数据中分离两个或多个类。LDA对二分类类问题非常有效，但扩展到两个以上的类可能会导致多重判别。

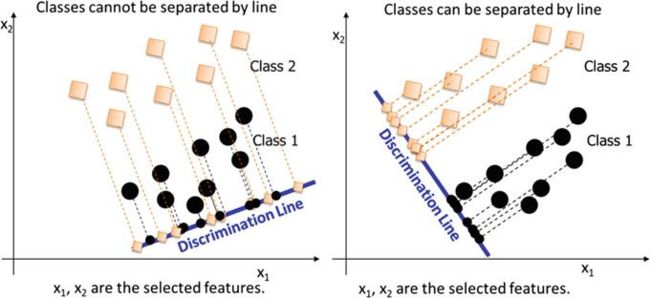
（图8.5 LDA工作原理示意图）

基于贝叶斯分类器的LDA判别函数最大限度地提高了给定特征度量值的类分配概率。

$f(x)={\mathrm{argmax}}_{j=1,\dots ,K}P(C=j\mid X=x)$（8.1）

$C$ 是类变量， $x$代表特征度量值，上述公式的想法是选择最大化条件概率的类 $j$， LDA 假设类数据服从高斯分布，虽然每个类都有不同的均值 ${\mu }_j$，但假设所有类都具备共同的协方差矩阵。

通过一些数学运算，可以证明判别条件 ${\hat{d}}_j(x)$可以表示为：

$\begin{array}{rl}{\hat{d}}_j(x)=& x^{\mathrm{T}}{\hat{\Sigma }}^{-1}{\hat{\mu }}_j-\frac{1}{2}\left({\hat{\mu }}_j^{\mathrm{T}}{\hat{\Sigma }}^{-1}{\hat{\mu }}_j\right)+\log \left({\hat{p}}_j\right)\\ =& a_j+b_j^{T}x\\ & \hat{f}(x)={\mathrm{argmax}}_{j=1,\dots ,K}{\hat{d}}_j(x)\end{array}$（8.2）

其中，$p_j$ 是 $j$类的概率，在变量上的符号“^”表示估计值，这些可以从数据中计算出来。

要将这个模型用作分类器，我们只需要从训练数据中估计出类的先验概率，这些先验概率通常是通过取每个类在训练数据中的比例来计算的。 例如，如果在 二分类问题中每个类使用相同数量的训练数据，那么每个类的先验概率将为 0.5。 类似地，也可以从数据中估计类均值。

可以看出，$f(x)$ 是特征度量值 $x$ 的线性函数，执行 LDA 的一种实用方法是通过公共协方差矩阵的特征值分解。 分类遵循以下几个步骤：

（1）估计先验类概率 ${\hat{p}}_j$ ，类均值 ${\hat{\mu }}_j$ ，以及公共协方差 $\hat{\Sigma }$ 。
（2）执行协方差的奇异值分解 $\hat{\Sigma }=UD{U}^{\mathrm{T}}$ ，其中 D 是对角线，U 是正交矩阵。
（3）变换类质心，使得 ${\tilde{\mu }}_j=D^{-1/2}{U}^{\mathrm{T}}{\hat{\mu }}_j$ 。
（4）使用关系 $\tilde{x}=D^{-1/2}{U}^{\mathrm{T}}x$ 转换查询点。
（5）按规则分类：${\min }_j\left(\frac{1}{2}{\Vert \tilde{x}-{\tilde{\mu }}_j\Vert }_2^2-\log \left({\hat{p}}_j\right)\right)$ 。
利用上述方法，可以对LDA的性能进行评估。例如，我们考虑两个分离良好（类内协方差小，类间协方差大）的类， 两类随机生成的数据如图 8.6 所示。

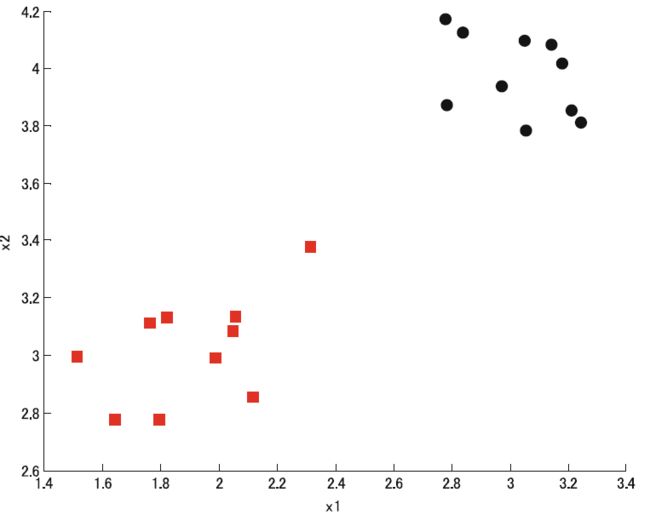
（图8.6 LDA示例数据，类1和类2分别用红色方框和黑色圆形表示）

LDA对数据的分类结果可以总结在表8.1的混淆矩阵中。

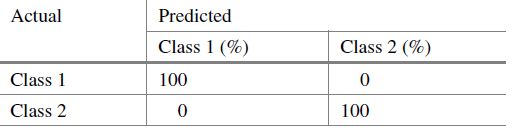
（表8.1 LDA分类结果的混淆矩阵）

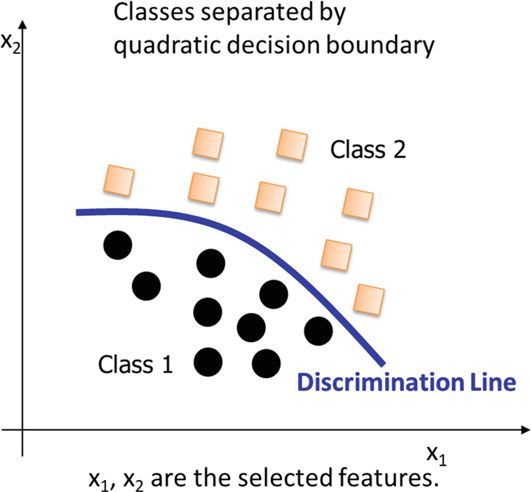
结果表明，LDA可以准确地对数据进行分类。 在这种情况下，可以找到区分这两个类的判别线，尽管 LDA 可以很好地处理分离良好的类，但它不能处理非线性决策边界， 数据分布假设也限制了 LDA 对问题子集的应用。

2. 二次判别分析 (QDA)

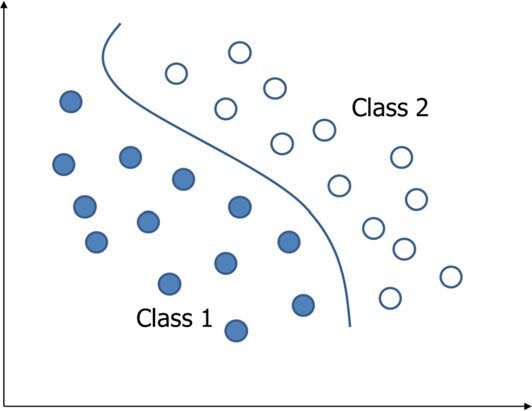
QDA可以对非线性问题正确地划分类，如图8.7所示，与LDA的唯一区别是，QDA使用的是二次判别函数，LDA使用的线性判别函数。

${\hat{d}}_j(x)=-\frac{1}{2}\ast \log \left(\left|{\sum }_j\right|\right)-\frac{1}{2}\ast {\left(x-{\mu }_j\right)}^{\mathrm{T}}{\sum }_j^{-1}\left(x-{\mu }_j\right)+\log \left({\hat{p}}_j\right)$
${\sum }_j=\frac{1}{n_j}\ast {\sum }_{k\in C_j}{\left(x_k-{\mu }_j\right)}^{\mathrm{T}}\left(x_k-{\mu }_j\right)$（8.3）

（图8.7可用QDA求解的类间非线性分离实例）

除了 QDA 之外，非线性函数还可以用作判别函数，从而产生所谓的非线性判别分析 (NDA)， 表 8.2 给出了判别分析方法的特点比较。

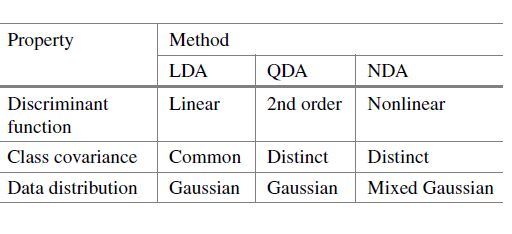
（表8.2判别分析方法性质比较）

8.2.3.支持向量机（SVM）

支持向量机(SVM)是基于统计学习理论的机器学习算法，它通过在多维空间中构建超平面来进行分类。该算法被引入来解决监督分类和回归问题。虽然支持向量机起源于图像识别，但迄今为止，它们已经扩展到包括遥感、雷达等领域。

一般来说，支持向量机从无限个潜在的边界中选择决策边界，在离超平面最近的数据点之间留下最大的余量(如图8.8)，这被称为“支持向量”。“支持向量机使用用于非线性分类问题的核函数，将训练数据转换为高维特征空间。在这一点上，支持向量机被认为属于内核方法，因为内核函数是用来最大化类之间的边界的。

从图 8.8 可以看出，希望最大化从决策边界 $w^{T}x+b=0$到两个类别中的任何一个的距离， 这可以通过最大化边距 $m=2/\Vert \mathbf{w}\Vert$来实现， 这种最大化的方法利用约束优化理论。其中，潜在问题可以表述如下：

设数据集 $x1,\dots ,xn$ 可用，数据的两个类标签由 $y_i=\{-1,1\}$定义， 然后，正确分类所有点的决策边界由下式给出：${\mathbf{y}}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\ge 1$ ，其中$\forall i$表示“对于所有$i$ ”。

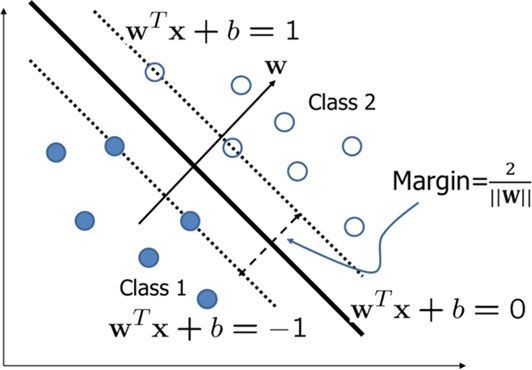
（图8.8可分离情况下的线性分离超平面，实圆属于第一类，白圆属于第二类。粗黑线表示分离类的最佳超平面，而虚线上的圆表示支持向量）

约束优化问题可以表述如下：

minimize: $\frac{1}{2}\mid \Vert \mathbf{w}{\Vert }^2$
subjectto $:{\mathbf{y}}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\ge 1\forall i$（8.4）

上述问题可以通过首先定义以下拉格朗日量来表述：

$L=\frac{1}{2}\Vert w\Vert 2+{\sum }_{i=1}^n{\alpha }_i\left(1-y_i\left(w^{\mathrm{T}}{x}_i+b\right)\right)$（8.5）

其中 ${\alpha }_i$ 是拉格朗日乘数。 拉格朗日定义了优化问题的解存在的必要条件。 每个约束都由一个拉格朗日乘子加权，任务是找到使函数$L$ 最小化的拉格朗日乘子，取 $L$ 对 $w2$ 和 $b$的导数，并将结果等同于零，我们得到解为：

$\mathbf{w}={\sum }_{i=1}^n{\alpha }_i{\mathbf{y}}_i{\mathbf{x}}_i{\sum }_{i=1}^n{\alpha }_i{\mathbf{y}}_i=0$（8.6）

将 $w$ 代入 $L$ ，可以证明：

$\mathrm{L}={\sum }_{i=1}^n{\alpha }_i{y}_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{i=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j(8.7)$（8.7）

原来的约束优化问题现在可以表述如下：

$\mathrm{maximize}:{\sum }_{i=1}^n{\alpha }_i{y}_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$
subjectto $:{\sum }_{i=1}^n{\alpha }_i{y}_i=0,{\alpha }_i\ge 0$（8.8）

上述问题中除了 所有变量都是已知的${\alpha }_i$，如果可以找到${\alpha }_i$ ，那么 $w$ 也可以确定，因此，可以计算边距 $m=2/\Vert \mathbf{w}\Vert$ 。 拉格朗日乘数 ${\alpha }_i$ 可以通过二次规划 (QP) 算法 获得，除了图 8.8 中所示的支持向量，所有其他样本的拉格朗日乘数都将为零。

当超平面是线性的并且类是完全可分离的时，上述过程很有效。 然而，在实践中并非总是如此，因此有必要修改优化标准以处理线性不可分和非线性问题，这种修改可以通过引入松弛变量和核函数来实现。

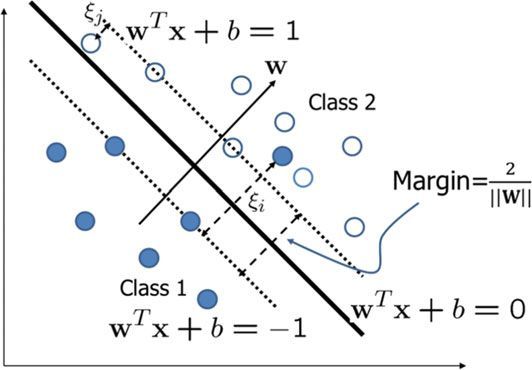
首先，对于线性不可分情况（图 8.9）可以引入松弛变量$\xi$。 松弛变量考虑了错误分类的样本。 尽管大多数样本仍然可以正确地线性分类，但只有少数样本（噪声）落入了错误的类别，那么优化问题现在可以表述为：

minimize : $\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C{\sum }_{i=1}^n{\xi }_i$
subjectto $:{\mathrm{y}}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\ge 1-{\xi }_i,{\xi }_i\ge 0$（8.9）

正则化参数 $C$控制 SVM 的复杂性和不可分离点的数量之间的平衡，这是通过交叉验证作为错误惩罚确定的。 因此， $C$控制最大化边际和最小化训练误差之间的平衡。 较小的 $C$ 值倾向于强调边缘而忽略训练数据中的异常值，而较大的 $C$值可能会过度拟合训练数据。

按照线性可分情况概述的步骤，优化问题变为：

maximize $:L(\alpha )={\sum }_{i=1}^n{\alpha }_i{\mathbf{y}}_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$ subjectto: ${\sum }_{i=1}^n{\alpha }_i{y}_i=0,C\ge {\alpha }_i\ge 0$ （8.10）

与线性可分情况一样，不可分情况也可以使用 QP方法求解。 对于非线性可分情况（图 8.10），核函数可用于获得可接受的解，核函数允许将分离的超平面转换为线性域，然后可以在其中执行计算。

（图8.9线性不可分情形的图解。松弛变量ξ增加了违反优化约束的惩罚）

然而，显式转换的计算成本很高，因此采用了“核技巧”，无需显式计算即可转换到内积空间。

假设核函数满足 Mercer 定理 ，Mercer 定理指出：当且仅当$K(x,y)$为半正定时，对称函数 $K(x,y)$可以表示为某个 $\Phi$的内积$K(x,y)=\Phi (x)\Phi (y)$。 这意味着 $n\times n$ 核矩阵，其中第 $(i,j)$ 项是 $K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$ 始终是半正定的，这反过来又保证了优化问题的解决方案的存在。

非线性情况的核函数通常由以下等式定义：

$K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\Phi \left({\mathbf{x}}_i\right)\Phi \left({\mathbf{x}}_j\right)$（8.11）

非线性优化问题可以表示如下：

$\mathrm{maximize}:L(\alpha )={\sum }_{i=1}^n{\alpha }_i{y}_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$
subjectto $:{\sum }_{i=1}^n{\alpha }_i{y}_i=0,C\ge {\alpha }_i\ge 0$（8.12）

除了正则化参数 $C$ 外，现在的问题还包括选择合适的核函数$K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$ 。典型内核的示例包括多项式、径向基函数（高斯）、反多次二次函数，以及在某种程度上的 sigmoid 函数（S型函数）。对基于核的方法的详细分析超出了本文的范围，但可以说，在选择核函数时，低阶多项式或径向基函数 (RBF) 可能会是一个很好的出发点。

虽然 SVM 最初是二分类器，但有几种方法可用于解决雷达传感器数据分类标准的多类问题：

（1）第一种方法是最常见和最简单的，称为一对多 (OAA)，这种方法对每个类和训练使用一个二进制 SVM。
（2）第二种方法称为一对一 (OAO) 或成对方法，在这种方法中，每个分类器都经过训练以分离一对类，并将所有分类结果组合成一个最终结果。
（3）第三种方法称为多类排序 SVM（或结构化 SVM）。

8.3 雷达目标识别技术的挑战与发展趋势

在目标识别方面存在一些挑战，在本文中，我们简要总结了其中的一些挑战，并简要介绍了当前的趋势，这些趋势都集中在寻找切实可行的解决方案上。

8.3.1 挑战

1.特征选择

特征选择是雷达识别的一大难题，可以在参考文献[1]中找到一些特性示例：

（1）一个特征来源是：提取目标周围的多个距离和速度检测数据的方差和标准差可以作为特征。然而，接收到的数据通常会受到噪声和杂波的干扰，因此，需要进行足够的预处理。

（2）另一个特征来源是：利用雷达反射的微多普勒特征。我们感兴趣的特征是平均速度(平均多普勒频率)、基本步态频率、步幅和雷达截面(RCS)，这些特征的提取通常通过**短时间傅里叶变换（STFT）**完成。当需要在目标中识别行人时，该方法是有效的。

2.识别率

对于汽车应用，大多数机器学习算法的识别率有时会低于70%，这些水平是不可接受的，特别是当考虑的目标之一是行人。错误分类可能会导致不可预测的系统行为，并增加与物体碰撞的概率。因此，识别速度在这种情况下，要求大于99%，这对于需要近乎完美识别率的自动驾驶系统来说尤其如此。

3.处理需求

雷达传感器的性能对处理要求很严格，雷达参数的选择对雷达性能有很大的影响。对于近程雷达，雷达数据存储一般小于1MB。此外，处理时间通常限制在50到100毫秒之间。这些雷达要求在选择处理算法时需要慎重考虑，这意味着内存密集型算法无法在当前的雷达架构中轻松实现。、

8.3.2目前的趋势

为了解决机器学习算法识别能力低、对新目标需要重新训练等问题，深度学习作为候选解决方案之一近年来被广泛研究。为了理解深度学习的起源，对这些算法在更广泛的人工智能图景中的位置进行一些深入了解是有意义的。人工智能领域包括机器学习和深度学习。人工智能有很多定义，但共同点是希望制造出具有一定程度人类智能的机器。因此，计算机科学家和工程师将人工智能定义为计算机系统执行智能任务的能力，其中包括计算机视觉、自然语言处理、机器学习、模式识别、机器人、专家系统和神经网络。

另一方面，机器学习(ML)是研究能够完成智能任务的计算机算法和统计模型。如前所述，这些算法可以分为监督学习、半监督学习和无监督学习。最后，深度学习起源于人工神经网络，而人工神经网络是沿着人类神经元建模的，称为感知器。

神经网络的细节超出了本文的范围，但是感知器需要几个二进制输入，并产生一个二进制输出，如图8.11所示。输出可以使用以下表达式计算:

output $=\{\begin{array}{l}0,{\sum }_{i=0}{w}_i{x}_i\le {\theta }_0\\ 1,{\sum }_{i=0}{w}_i{x}_i>{\theta }_0\end{array}$（8.13）

其中，$x_0=0$ 和 ${\theta }_0$是预定阈值。

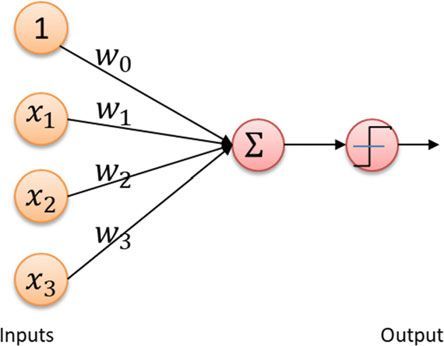
（图8.11简单感知器模型）

神经网络的概念可以扩展到多层感知器以产生复杂的决策，如图 8.12 所示。

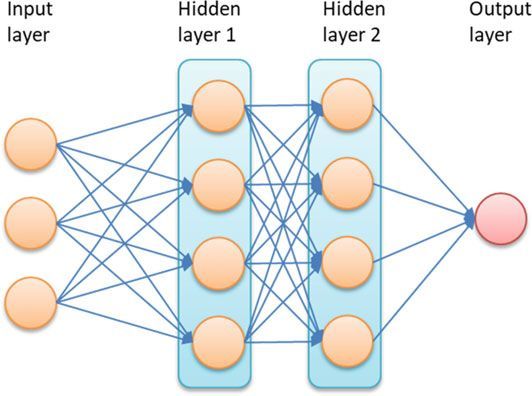
（图8.12多层感知器模型示例）

深度学习网络与神经网络的不同之处在于所使用的节点层的数量，这就引入了“深度”的概念。神经网络通常有一到两层隐藏层，用于监督预测或分类。深度学习网络可以有多个隐藏层，具有无监督训练的可能性，如图8.13所示。

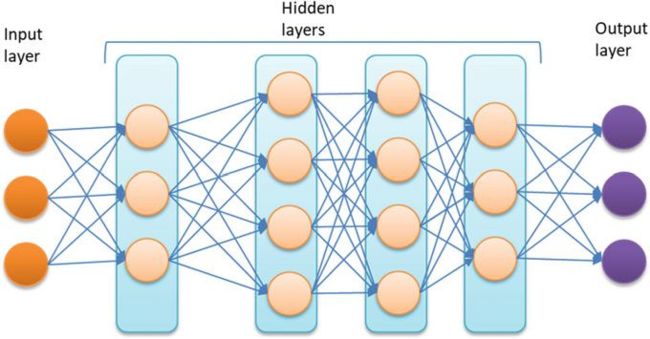
（图8.13深度神经网络模型示例）

广泛使用的深度学习架构的例子包括深度神经网络(DNN)、深度信念网络(DBF)和循环神经网络(RNN)。与传统的神经网络相比，DNN的主要优点是能够在网络中学习复杂的无人监督的任务 ，然而建立网络需要大量的数据，另外，高计算复杂度是一个很大的负担，在试图分析算法时出现困难，存在无法准确预测输出等挑战。

**对于汽车应用而言，DNN具有广阔的前景，因为算法的计算强度和汽车雷达环境的复杂性，目前直接应用于汽车雷达仍处于研究阶段。**有兴趣的读者可以在文献[28,29]中找到关于DBM和RNN的详细信息，值得注意的是，RNN在自然语言处理(NLP)中取得了很好的成果。

感谢阅读，如果本文对你有帮助，希望能够给我点一个赞！

参考文献

1. Heuel, S., Rohling, H.: Pedestrian recognition based on 24 GHz radar sensors. In: 11-th International
   Radar Symposium, 12 Aug 2010
2. Chen, V., et al.: Micro-doppler effect in radar: phenomenon, model, and simulation study. IEEE
   Trans. Aerosp. Electron. Syst. 42(1), 2–21 (2006)
3. Bilik, I., Tabrikian, J.: Radar target classification using doppler signatures of human locomotion
   models. IEEE Trans. Aerosp. Electron. Syst. 43(4), 1510–1522 (2007)
4. Yan, H., Doerr, W., Ioffe, A., Clasen, H.: Micro-doppler based classifying features for automotive
   radar VRU target classification. In: 25th International Technical Conference on the
   Enhanced Safety of Vehicles (ESV), Detroit Michigan, United States (2017)
5. Bishop, C.M.: Neural Networks for Pattern Recognition. Oxford University Press, Inc., New
   York (1995)
6. Scikit-learn, scikit-learn: machine learning in Python
7. OpenCV, https://www.learnopencv.com/
8. Cover, T., Hart, P.: Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 13(1),
   21–27 (1967)
9. Fisher, R.A.: The use of multiple measurements in taxonomic problems. Ann. Eugen. 7,
   179–188 (1936)
10. Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning. Springer (2008)
11. Cortes, C., Vapnik, V.: Support-vector network. Mach. Learn. 20(3), 273–297 (1995)
12. Huang, Z., Lee, B.G.: Combining non-parametric models for multisource predictive forest
    mapping. Photogram. Eng. Remote Sens. 70, 415–425 (2004)
13. Boser, B.E., Guyon, I.M., Vapnik, V.N.: A training algorithm for optimal margin classifiers.
    In: Fifth Annual Workshop on Computational Learning Theory, pp. 144–152. ACM (1992)
14. Vapnik, V.N.: The Nature of Statistical Learning Theory. Wiley, New York (1998)
15. Camps-Valls, G., Bruzzone, L.: Kernel-based methods for Hyperspectral image classification.
    IEEE Trans. Geosci. Remote Sens. 43(6), 1351–1362 (2005)
16. Bruzzone, L., Persello, C.: A novel context-sensitive semi-supervised SVM classifier robust to
    mislabeled training samples. IEEE Trans. Geosci. Remote Sens. 47(7) (2009)
17. Liu, J., et al.: Radar target classification using support vector machine and subspace methods.
    IET Radar Sonar Navig. 9(6), 632–640 (2015)
18. Vapnik, V.N.: Statistical Learning Theory. Wiley, New York (1998)
19. Burges, C.J.C.: A Tutorial on Support Vector Machines for Pattern Recognition, pp. 1–43.
    Kluwer Academic Publishers, Boston (1998)
20. Fioranelli, F., Ritchie, M., Griffiths, H.: Bistatic human micro doppler signatures for classification
    of indoor activities. In: 2017 IEEE Radar Conference (Radar Conf), Seattle,WA, USA,
    08–12 May 2017
21. Bloecher, H.-L., Andres, M., Fischer, C., Sailer, A., Goppelt, M., Dickmann, J.: Impact of
    system parameter selection on radar sensor performance in automotive applications.Adv.Radio
    Sci. 10, 33–37 (2012)
22. Singh, J., Ginsburg, B., Rao, S., Ramasubramanian, K.: AWR 1642 mm wave sensor: 76–81-
    GHz radar-on-chip for short-range radar applications. Texas Instruments, May 2017
23. Hinton, G.E., Salakhutdinov, R.R.: Reducing the dimensionality of data with neural networks.
    Science 313(5786), 504–507 (2006)
24. Hinton, G.E., Osindero, S., Teh, Y.: A fast learning algorithm for deep belief nets. Neural
    Comput. 18 (2006)
25. Furukawa, H.: Deep learning for end-to-end automatic target recognition from synthetic aperture
    radar imagery. IEICE Technical Report, vol. 117, No. 403, SANE 2017-92, pp. 35–40
    (2018)
26. Angelov, A.,Robertson, A., Murray-Smith,R., Fioranelli, F.: Practical classification of different
    moving targets using automotive radar and deep neural networks. IET Radar, Sonar Navig.
    12(10), 1082–1089 (2018)
27. Wheeler, T.A., Holder, M.F., Winner, H., Kochenderfer, M.J.: Deep stochastic radar models.
    In: IEEE Intelligent Vehicles Symposium (IV) (2017)
28. Salakhutdinov, R., Hinton, G.E.: Deep Boltzmann Machines. AISTATS, pp. 448–455 (2009)
29. Graves, A., Mohamed, A., Hinton, G.E.: Speech recognition with deep recurrent neural networks.
    In: ICASSP, pp. 6645–6649 (2013)