雷达信号处理算法：静态杂波滤除（附MATLAB代码和数据）

本文编辑：调皮哥的小助理

本期文章将介绍三种雷达信号处理常用的静态杂波滤方法的基本原理，分别是零速通道置零法、动目标显示（MTI）以及相量均值相消算法（平均相消算法），并分析了静态杂波的滤除效果，以及三种方法的优缺点和应用场景，最后提供了一个MATLAB程序和数据以供读者学习参考。

数据说明：本文所采用的数据为雷达采集室内人员目标运动的一帧数据，采用的硬件平台为IWR1642，其中数据是通过串口直接输出，由MATLAB接收并处理。相关的操作和下面的链接中的操作是近似的，只是本文仅对静态杂波滤除算法做分析。

调皮连续波：TI单芯片毫米波雷达xWR1642人员检测代码分析（5）——串口单帧数据采集代码详解

1.零速通道置零法

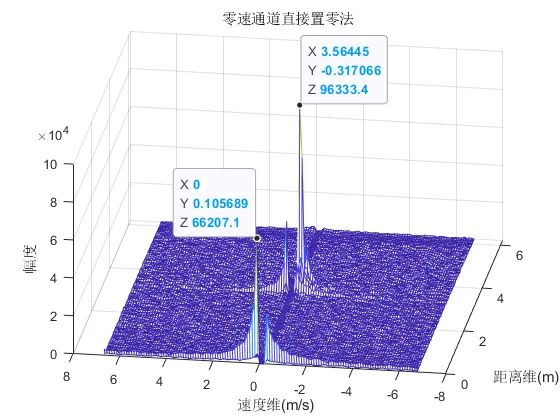
零速通道置零法，是指在2D-FFT（速度维FFT）后直接将R-V谱矩阵（RD图）速度通道中的零速通道或零速附近通道置零，此操作意味着静止目标或者低速目标会直接从R-V谱矩阵中消失。零速通道置零法操作简单，易于理解。

如图1所示，是未经过任何处理的R-V谱矩阵，其中室内人员目标在3.5米左右，速度为-0.317m/s，靠近雷达运动。

（图1 R-V谱矩阵（未经过静态杂波滤除））

图1中信号的直流分量幅值很高，目标的幅度被直流分量严重压制，在进行后续的CFAR处理之前最好能够将信号的直流分量去除，便于提高雷达的性能。图2所示是零通道置零法的效果，其中本程序对零速通道以及零速通道相邻的一个通道都置为零。零速通道置零法对目标的幅度没有发生改变，对直流分量有一定的抑制效果，但对目标的微多普勒信息有一定的损失。因此，采用这种最简单的方法需要考虑具体的应用场景。

（图2 零速通道置零法）

微多普勒信息，对于不同的雷达具有不同的作用。例如，对于室内人员检测雷达，则微多普勒信息就显得非常重要，因为人体目标是非刚体物体，其身体各个部分的运动会带来许多的微多普勒效应，因此保留这部分信息对于后续的信号处理或者数据处理都具有非常重要的意义。对于高速目标，如交通流量检测雷达，微多普勒信息就显得不那么重要 ，因为汽车运动的速度是非常快的。关于雷达微多普勒的效应，更多内容可以阅读Victor C. Chen的《雷达中的微多普勒效应》一书，需要本书可私信调皮哥。

2.动目标显示（MTI）

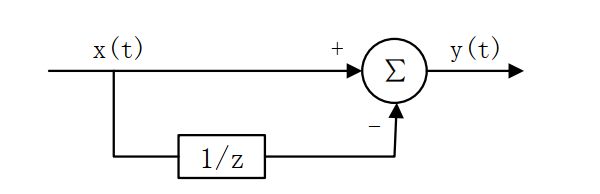
MTI是雷达工程师们熟稔于心的雷达信号处理算法，基本上没有不了解的。MTI是指利用杂波抑制滤波器来抑制杂波，提高雷达信号的信杂比，以利于运动目标检测的技术。由于杂波谱通常集中在直流分量和雷达重复频率的整数倍处，而 MTI 滤波器利用杂波与运动目标的多普勒频率的差异，使得滤波器的频率响应在直流和PRF（脉冲重复频率） 的整数倍处具有较深的阻带， 而在其他频点的抑制较弱， 从而通过较深的“凹口”抑制静止目标和静物杂波。在实验中，通常采用两脉冲对消器，也称一次对消器,其滤波器结构如下图3所示。

（图 3 一次对消滤波器结构图）

一次对消器的时域表达式和传递函数如下：

$y(n)=x(n)-x(n-1)$
$H(z)=1-z^{-1}$

MTI的核心原理就是静止目标的相位不会发生变化，而运动目标的相位与静止目标不同，因此相邻两个脉冲做差会把相同的相位值减掉，留下的就是运动目标的相位，从而达到滤除静止目标的功能。

MTI的效果如图4所示，其中信号的直流分量部分得到了良好的抑制，但同时目标的幅值也受到了同样的影响，因为在一次对消过程中，相邻的脉冲相减其实除了相位得到了消除，还有“复数绝对值”的削弱。另外，MTI由于仅对零速通道附近的信号“陷波”，而对于高速通道保持不变，因此得到图4的结果中背景噪声显得非常杂乱。

（图4 MTI一次对消效果）

3.相量均值相消算法（平均相消算法）

相量均值相消算法，也被称为平均相消算法，其实现的原理为：静止目标到雷达天线的距离是不变的，每一束接收脉冲上静止目标的时延也是不变的，对所有接收脉冲求平均就可以得到参考的接收脉冲，然后用每一束接收脉冲减去参考接收脉冲就可以得到目标回波信号，核心思想是求均值做差。

其实现的过程为：首先对所有接收脉冲求平均得出参考接收脉冲，接着利用每一束接收脉冲减去参考接收脉冲就可以得到目标回波信号，参考接收脉冲的表达式为：

$C[m]=\frac{1}{N}{\sum }_{i=1}^{N}R[m,i]$

其中，m为快时间维（距离维）采样点，i为慢时间维（速度维）时间采样点，相量均值相消算法的公式为：​

R[m, n]=R[m, n]-C[m]。

相量均值相消的算法原理模型如图5所示，倘若目标为静止目标，则chirp回波信号的相位相同，相量求和后累加得到的均值会很大，如$\left(n_1+n_2+n_3\right)/3$ ，则每个chirp信号减完均值之后信号幅度变得非常小。假设目标是运动目标或者微动目标，由于目标运动会导致每个调频脉冲信号间的相位不同，其相量求和累加后会出现抵消，则其均值会很小，如 $\left(m_1+m_2+m_3\right)/3$ ，每个chirp信号减完均值后幅值影响不大。因此，运动或微动的目标就会在速度维傅里叶变换后变得“突出”。

（图5 相量均值相消算法模型）

综上所述，MTI和相量均值相消算法两种算法在原理的核心思想上有些许近似，最大的区别为：MTI是直接利用相位的差值消除静态杂波，而相量均值相消算法是通过相量叠加再求平均然后做差，去除静态杂波。因此MTI仅仅是抑制了静态目标的相位，对于微动目标不友好。而相量均值相消算法则通过求均值，在抑制静止目标相位的同时极大提高了动目标或者微动目标的信噪比。

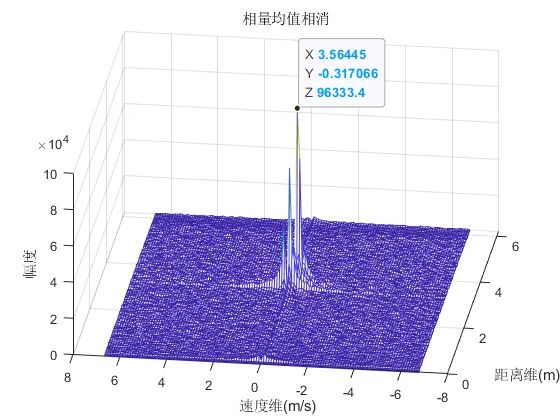
如图6所示，是相量均值相消算法的效果，信号的直流分量得到了一定程度的抑制，但整体抑制效果没有MTI那么明显。相量均值相消算法最优的特点是对目标的幅度没有削弱作用，但其背景噪声比较干净，同时对微多普勒的信息保留的比较完整，完全让目标保持了较高的信噪比。

（图6 相量均值相消算法效果）

对于人员目标的检测，建议采用这种算法。如图7所示，是相量均值相消算法并去除了直流分量后的效果，基本上可以达到非常理想的效果。

（图7 相量相消后并进行直流分量去除效果）

4.MATLAB代码

数据部分由于在文章中无法分享，因此本文所用到的MTALBA代码和数据，可关注公众号：调皮的连续波，回复"0414"获得。

我是调皮哥，感谢阅读。

%% 作者：调皮连续波
%% 公众号：调皮的连续波
%% 时间2022年04月
%%
clc;
close all;
clear all;
%% 雷达参数
Tx_Number = 2; %发射天线
Rx_Number = 4; %接收天线
Range_Number = 128; %距离点数（每个chirp 128个点）
Doppler_Number = 128; %多普勒通道数
global Params;
Params.NChirp = Doppler_Number; %1帧数据的chirp个数
Params.NChan = Rx_Number; %RxAn数,ADC通道数
Params.NSample = Range_Number; %每个chirp ADC采样数
Params.Fs = 2.5e6; %采样频率
Params.c = 3.0e8; %光速
Params.startFreq = 77e9; %起始频率
Params.freqSlope = 60e12; %chirp的斜率
Params.bandwidth = 3.072e9; %真实带宽
Params.lambda=Params.c/Params.startFreq; %雷达信号波长
Params.Tc = 144e-6; %chirp周期
global FFT2_mag;
%% 坐标计算
[X,Y] = meshgrid(Params.c*(0:Params.NSample-1)Params.Fs/2/Params.freqSlope/Params.NSample, …
(-Params.NChirp/2:Params.NChirp/2 - 1)Params.lambda/Params.Tc/Params.NChirp/2);
adc_data =load(‘angle_15.mat’);
Data_dec=(adc_data.prompt_1); %将16进制转换为10进制
%% 数据读取、拆分、组合
Data_zuhe=zeros(1,Tx_NumberRx_NumberDoppler_NumberRange_Number2); %建立计算存储数据的空矩阵
for i=1:1:Tx_NumberRx_NumberDoppler_NumberRange_Number2
Data_zuhe(i) = Data_dec((i-1)2+1)+Data_dec((i-1)2+2)256;%两个字节组成一个数，第二个字节乘以256相当于左移8位。
if(Data_zuhe(i)>32767)
Data_zuhe(i) = Data_zuhe(i) - 65536; %限制幅度
end
end
%% 分放数据
ADC_Data=zeros(Tx_Number,Doppler_Number,Rx_Number,Range_Number2); %建立计算存储数据的空矩阵
for t=1:1:Tx_Number
for i=1:1:Doppler_Number
for j=1:1:Rx_Number
for k=1:1:Range_Number2 %实部虚部
ADC_Data(t,i,j,k) = Data_zuhe(1,(((t-1)Doppler_Number+(i-1))Rx_Number+(j-1))Range_Number2+k);%时域数据排列顺序为 TX1 TX2
end
end
end
end
%% 打印全部的实虚数据
Re_Data_All=zeros(1,Range_NumberDoppler_NumberTx_NumberRx_Number); %建立计算存储数据的空矩阵
Im_Data_All=zeros(1,Range_NumberDoppler_NumberTx_NumberRx_Number); %建立计算存储数据的空矩阵
% 虚部实部分解
for i=1:1:Tx_NumberRx_NumberDoppler_NumberRange_Number
Im_Data_All(1,i) = Data_zuhe(1,(i-1)2+1);
Re_Data_All(1,i) = Data_zuhe(1,(i-1)2+2);
end
% 原始信号实部、虚部图形绘制
% figure()
% subplot(2,1,1);
% plot(Im_Data_All(1,1:3000));title(‘实部波形’);
% xlabel(‘采样点数’);
% ylabel(‘幅度’);
% subplot(2,1,2);
% plot(Re_Data_All(1,1:3000),‘r’);title(‘虚部波形’);
% xlabel(‘采样点数’);
% ylabel(‘幅度’);
%% 打印分组后的实虚数据 数据结构为：2T4R在TX2组的16个脉冲数据
Re_Data=zeros(Doppler_Number,Range_Number); %建立计算存储数据的空矩阵
Im_Data=zeros(Doppler_Number,Range_Number); %建立计算存储数据的空矩阵
for chirp=1:Doppler_Number %查看所在chirp的数据
for j=1:1:Tx_Number
for k=1:1:Rx_Number
for i=1:1:Range_Number
Re_Data(chirp,i) = ADC_Data(j,chirp,k,(i-1)2+2);
Im_Data(chirp,i) = ADC_Data(j,chirp,k,(i-1)2+1);
end
end
end
end
%% 虚部+实部数据重组得到复信号
ReIm_Data = complex(Re_Data,Im_Data); %这里只用虚拟天线的最后一组数据。原本数据大小应该是162568=32768，现在只有162561=4096。
ReIm_Data_All =complex(Re_Data_All,Im_Data_All);
ReIm_Data_all1 = zeros(Range_Number,Doppler_Number,4);
ReIm_Data_all2 = zeros(Range_Number,Doppler_Number,4);
%% 虚拟阵列重组 4通道->8通道
for nn=1:4
for mm=1:Range_Number
ReIm_Data_all1(mm,:,nn) = ReIm_Data_All((nn-1)*Range_Number+ ((mm-1)4Range_Number+1)(mm-1)4Range_Number+Range_Number)+(nn-1)*Range_Number );
ReIm_Data_all2(mm,:,nn) = ReIm_Data_All((nn-1)*Range_Number+131072/2+((mm-1)4Range_Number+1):131072/2+((mm-1)4Range_Number+Range_Number) +(nn-1)*Range_Number );
end
end
ReIm_Data_All = cat(3,ReIm_Data_all1(:,:,1:4), ReIm_Data_all2(:,:,1:4));
%% 1D FFT
fft1d= zeros(Doppler_Number,Range_Number,8);
for qq =1:8
for chirp_fft=1:Doppler_Number
fft1d(chirp_fft,:,qq) = fft((ReIm_Data_All(chirp_fft,:,qq)));
end
end
FFT1_mag=abs(fft1d(:,:,1));
figure(1);
mesh(FFT1_mag);
xlabel(‘采样点数’);ylabel(‘脉冲数’);zlabel(‘幅度’);
title(‘距离维FFT结果’);
%% MTI 动目标显示
fft1d_MTI= zeros(Range_Number,Doppler_Number,8);
for cc =1:8
for ii =1:Doppler_Number-1
fft1d_MTI (ii,:,cc) = fft1d(ii+1,:,cc)-fft1d(ii,:,cc);
end
end
%
%
% mesh(abs(ReIm_Data_All(:,:,1)));
%% 相量均值相消算法-静态杂波滤除
fft1d_avg = zeros(128,128,8);
for n=1:8
avg = sum(fft1d(:,:,n))/128;
for chirp=1:128
fft1d_avg(chirp,:,n) = fft1d(chirp,:,n)-avg;
end
end
% figure;
% mesh(X,Y,abs(fft1d_jingtai(:,:,1)));
% fft1d =fft1d_jingtai;
%%
%% 2D FFT
fft2d= zeros(Doppler_Number,Range_Number,8);
for kk=1:8
for chirp_fft=1:Range_Number
fft2d(:,chirp_fft,kk) =fftshift( fft((fft1d(:,chirp_fft,kk)))); %未经过静态杂波滤除
fft2d_MTI(:,chirp_fft,kk) =fftshift( fft((fft1d_MTI(:,chirp_fft,kk)))); %MTI
fft2d_avg(:,chirp_fft,kk) =fftshift( fft((fft1d_avg(:,chirp_fft,kk)))); %相量均值法
end
end
figure(2);
fft2d_0 =abs(fft2d(:,:,1));
mesh(X,Y,fft2d_0);
xlabel(‘距离维(m)’);ylabel(‘速度维(m/s)’);zlabel(‘幅度’);
title(‘R-V谱矩阵’);
figure(3);
fft2d_0 =abs(fft2d(:,:,1));
fft2d_0(63:65,:)=0;
mesh(X,Y,fft2d_0);
xlabel(‘距离维(m)’);ylabel(‘速度维(m/s)’);zlabel(‘幅度’);
title(‘零速通道直接置零法’);
figure(4);
mesh(X,Y,abs(fft2d_MTI(:,:,1)));
xlabel(‘距离维(m)’);ylabel(‘速度维(m/s)’);zlabel(‘幅度’);
title(‘MTI’);
figure(5);
mesh(X,Y,abs(fft2d_avg(:,:,1)));
xlabel(‘距离维(m)’);ylabel(‘速度维(m/s)’);zlabel(‘幅度’);
title(‘相量均值相消’);
%直流分量去除 相量均值相消算法-静态杂波滤除
figure(6)
fft2d_avg(:,1,1) =0;
mesh(X,Y,abs(fft2d_avg(:,:,1)));
xlabel(‘距离维(m)’);ylabel(‘速度维(m/s)’);zlabel(‘幅度’);
title(‘相量均值相消’);