【机器学习】单细胞-ZINB(零膨胀负二项分布)
目录
- 1 前言
- 2 正态分布
- 3 泊松分布
- 4 负二项分布
- 5 零膨胀负二项分布
- 6 应用
- 7 参考文献
1 前言
单细胞RNA测序(single-cell RNA-seq,scRNA-seq)数据是非常有特点的数据,具有很高的稀疏性(high sparsity),具体表现为0非常多(zero inflation)。对于数据的分布给出合理的假设是非常关键的工作,是下游分析的基础。显然对于scRNA-seq的reads count数据,最常用的正态分布是不合理的。首先正态分布描述的是连续型数据,而reads count数据是离散的;其次reads count数据的取值只能为非负整数。经过不断的尝试,ZINB被证明是一种可以较好的描述scRNA-seq数据的模型,并且作为一些更advanced的模型的基础。本文多有参考其他博客内容,相关参考内容一并列在参考文献部分,如有侵权请联系删除。
2 正态分布
说起分布,人们的第一反应大概都是正态分布。因为简单分布中正态分布最能符合现实生活中很多变量的观测。另外根据中心极限定理,如果一个特定事件受多个因素的影响,而每个因素对结果的影响都很小的时候,各种因素作用的和服从正态分布。但是细胞中RNA数量的值是离散的,而正态分布是连续分布。另外,scRNA-seq数据往往不是对称的,这与正态分布也不相吻合。因此,正态分布不适合用作scRNA-seq数据分布。
不过不同细胞转录出的RNA的量往往存在数量级上的差异,因此在数据分析时常常将数据做对数变换: x ′ = l o g x x^{'}=logx x′=logx ,而人们发现变换后的结果近似服从正态分布,因此scRNA-seq数据也被认为是服从对数正态(log-normal)分布的。
3 泊松分布
人们也尝试从测序的机理上来建模scRNA-seq数据的分布。如下图所示,一个细胞中部分基因各自转录出若干RNA,假设每条RNA被测序工具捕捉到的概率为 p p p,那么这一事件服从Bernoulli分布(二项分布);而从总数为 n n n 的所有RNA中捕捉到Gene1对应的RNA数量 n g n_g ng就服从二项分布:
n g 1 ∼ Binomial ( n , p ) n_{g 1} \sim \operatorname{Binomial}(n, p) ng1∼Binomial(n,p)
而一个细胞中转录出的RNA数量 n n n非常多,捕捉到某一条特定RNA的概率 p p p也相当小,因此二项分布就近似成为了泊松分布(泊松分布由二项分布推导而来,二者之间有紧密的联系。当二项分布的 n n n很大而 p p p很小时,泊松分布可作为二项分布的近似,其中 λ λ λ为 n p np np。通常当 n ≧ 20 , p ≦ 0.05 n≧20,p≦0.05 n≧20,p≦0.05时,就可以用泊松公式近似得计算):
n g 1 ∼ Poisson ( λ = n p ) n_{g 1} \sim \operatorname{Poisson}(\lambda=n p) ng1∼Poisson(λ=np)
P o i s s o n ( X = k ) = λ k k ! e − λ , k = 0 , 1 , ⋯ Poisson(X=k)=\frac{\lambda^{k}}{k !} e^{-\lambda}, k=0,1, \cdots Poisson(X=k)=k!λke−λ,k=0,1,⋯

(图片来源见参考文献【2】)
泊松分布的参数 λ λ λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。但泊松分布中均值始终等于方差,这一点不符合scRNA-seq数据的实际情况。下图展示了scRNA-seq数据的实际分布情况(散点,每个点代表一个基因对应RNA数量的统计量)和泊松分布的理论分布(直线)。可以看到,二者差别非常大,随着RNA均值的增加,其方差和均值之间的差距越来越大,这一现象称为"Over-dispersion"(过度分散)。因此我们仍然需要寻找更合理的分布来拟合scRNA-seq数据。
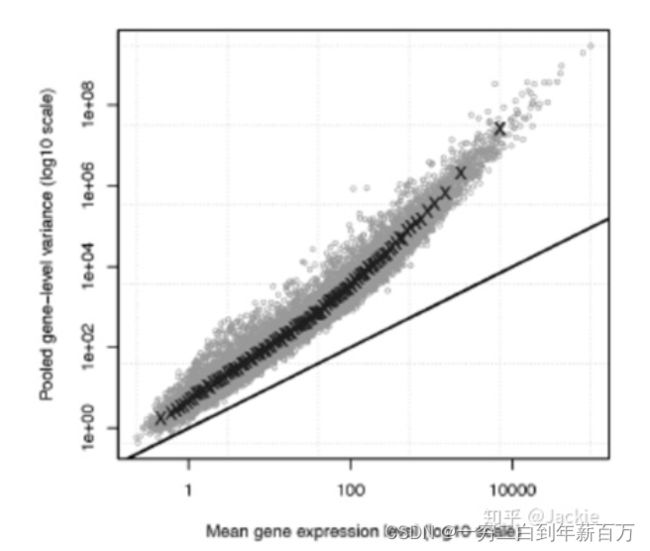
图片来源见参考文献【2】
4 负二项分布
进一步思考,在泊松分布中均值等于方差,而唯一参数 λ \lambda λ的值是不变的,如果它是变化的呢?经过一番探索后,人们发现如果 λ \lambda λ的先验分布取伽马分布的时候,即 λ ∼ Gamma ( α , β ) \lambda \sim \operatorname{Gamma}(\alpha, \beta) λ∼Gamma(α,β),后验分布满足负二项分布,因此负二项分布也称为Gamma-Possion分布。负二项分布包含两个参数: N B ( r , p ) N B(r, p) NB(r,p),其均值为:
μ = p r 1 − p \mu=\frac{p r}{1-p} μ=1−ppr
方差为:
σ 2 = p r ( 1 − p ) 2 = μ + μ 2 r \sigma^{2}=\frac{p r}{(1-p)^{2}}=\mu+\frac{\mu^{2}}{r} σ2=(1−p)2pr=μ+rμ2
均值不等于方差,因此可以解决scRNA-seq数据中over-dispersion的问题。同时负二项分布可以更好地拟合多种数据分布,如下图所示:

图片来源见参考文献【2】
负二项分布算是scRNA-seq数据分析的模型中广泛应用的数据分布了,由此开发出的差异表达与缺失值填补(单细胞领域习惯称为imputation)方法实用性也更强
5 零膨胀负二项分布
在广泛应用负二项分布的同时,人们也发现scRNA-seq数据还有一个特点,那就是零值非常多,下图给出了一个真实scRNA-seq数据中零表达基因比例的直方图

图片来源见参考文献【2】
由于基因表达数据中的零值既可能来自生物过程中不表达的基因(称为True Zero),还可能来自测序过程中由于技术原因导致的丢失(称为False Zero 或者Dropout Zero),因此人们尝试在NB模型中加入一个零膨胀因子,用零膨胀负二项分布(Zero-Inflated Negative Binomial)来建模scRNA-seq数据:
f Z I N B ( m ∣ θ , r , p ) = θ ⋅ I 0 ( m ) + ( 1 − θ ) ⋅ f N B ( m ∣ r , p ) f_{Z I N B}(m \mid \theta, r, p)=\theta \cdot I_{0}(m)+(1-\theta) \cdot f_{N B}(m \mid r, p) fZINB(m∣θ,r,p)=θ⋅I0(m)+(1−θ)⋅fNB(m∣r,p)
其中 θ \theta θ表征零值的比例, r , p r, p r,p为负二项分布的参数, I 0 ( m ) I_{0}(m) I0(m)为示性函数,当自变量为0时值为1,否则为0。
对于上面提到的真零假零的问题,ZINB模型也给予了回答,假设测序过程中RNA的捕获率为 β \beta β,那么不同 对应的分布如下图所示:
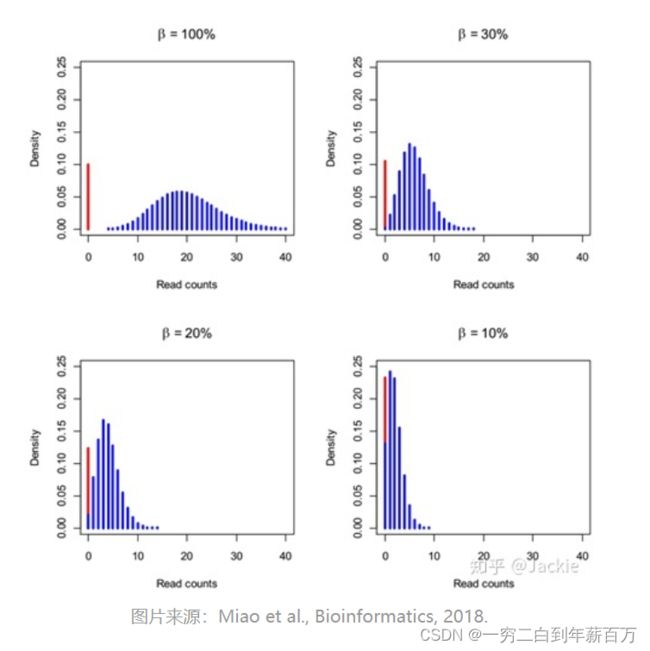
红色bar表示真实不表达基因产生的0值,蓝色bar为负二项分布,当捕获率不断降低时,NB分布会左移向0值靠拢,产生“假零”。而分析ZINB中两个部分的比例可以计算一个基因零值是假零的概率(Dropout Rate)。
d = ( 1 − θ ) ⋅ f N B ( 0 ∣ r , p ) θ + ( 1 − θ ) ⋅ f N B ( 0 ∣ r , p ) d=\frac{(1-\theta) \cdot f_{N B}(0 \mid r, p)}{\theta+(1-\theta) \cdot f_{N B}(0 \mid r, p)} d=θ+(1−θ)⋅fNB(0∣r,p)(1−θ)⋅fNB(0∣r,p)
6 应用
参考文献【4】
7 参考文献
[1]ZINB(Zero-inflated Negative Binomial)
[2]单细胞RNA-seq数据分布的选择
[3]泊松分布
[4]【论文阅读】 Single-cell RNA-seq denoising using a deep count autoencoder.
[5]RNA-seq中的那些统计学问题(一)为什么是负二项分布?