OpenCV —— 阈值分割(直方图技术法,熵算法,Otsu,自适应阈值算法)
阈值分割
-
- 1. 全局阈值分割
-
- 直方图技术法
- 熵算法
- Otsu算法
- 2. 局部阈值分割
-
- 自适应阈值
阈值的分割的核心就是如何选取阈值,选取正确的阈值时分割成功的关键。可以使用手动设置阈值,也可以采用直方图技术法、Otsu算法、熵算法自动选取全局阈值,也可以采用自适应阈值算法自动选取局部阈值。
1. 全局阈值分割
设定一个阈值,将图像中小于阈值的设为 255(白色),将图像中大于阈值的设为0(黑色);或者反过来,小于阈值的设为0,大于阈值的设为255。
OpenCV 函数:
threshold(InputArray src, OutputArray dst, double thresh, double maxval, int type)
| 参数 | 解释 |
|---|---|
| src | 输入矩阵(多通道、8位或32位浮点) |
| dst | 输出矩阵,即阈值分割后的矩阵 |
| thresh | 阈值 |
| maxVal | 与THRESH_BINARY和THRESH_BINARY_INV阈值类型一起使用的最大值。 |
| type | 类型,如下描述 |
-
THRESH_BINARY
dst ( x , y ) = { maxval if src( x , y ) > thresh 0 otherwise \text{dst} (x,y) = \begin{cases} \text{maxval} & \text{if src($x,y$) > thresh} \\ 0 & \text{otherwise} \end{cases} dst(x,y)={maxval0if src(x,y) > threshotherwise -
THRESH_BINARY_INV
dst ( x , y ) = { 0 if src( x , y ) > thresh maxval otherwise \text{dst} (x,y) = \begin{cases} 0 & \text{if src($x,y$) > thresh} \\ \text{maxval} & \text{otherwise} \end{cases} dst(x,y)={0maxvalif src(x,y) > threshotherwise -
THRESH_TRUNC
dst ( x , y ) = { threshold if src( x , y ) > thresh src ( x , y ) otherwise \text{dst} (x,y) = \begin{cases} \text{threshold} & \text{if src($x,y$) > thresh} \\ \text{src}(x,y) & \text{otherwise} \end{cases} dst(x,y)={thresholdsrc(x,y)if src(x,y) > threshotherwise -
THRESH_TOZERO
dst ( x , y ) = { src ( x , y ) if src( x , y ) > thresh 0 otherwise \text{dst} (x,y) = \begin{cases} \text{src}(x,y) & \text{if src($x,y$) > thresh} \\ 0 & \text{otherwise} \end{cases} dst(x,y)={src(x,y)0if src(x,y) > threshotherwise -
THRESH_TOZERO_INV
dst ( x , y ) = { 0 if src( x , y ) > thresh src ( x , y ) otherwise \text{dst} (x,y) = \begin{cases} 0 & \text{if src($x,y$) > thresh} \\ \text{src}(x,y) & \text{otherwise} \end{cases} dst(x,y)={0src(x,y)if src(x,y) > threshotherwise -
THRESH_MASK
-
THRESH_OTSU
使用 Otsu 算法选取最优阈值,可与上述任一一种 type 组合
-
THRESH_TRIANGLE
使用 Triangle 算法选取最优阈值,可与上述任一一种 type 组合。与下面要讲的直方图技术法类似。
比如 type=THRESH_OTSU + THRESH_BINARY ,即先用 Otsu 算法自动计算出阈值,然后利用该阈值采用 THRESH_BINARY 规则,默认采用 THRESH_BINARY。
Python 示例
import numpy as np
import cv2
src = np.array([[123,234,68],[33,51,17],[48,98,234],[129,89,27],[45,167,134]],np.uint8)
#手动设置阈值
threshold = 150
maxval = 255
dst = cv2.threshold(src, threshold, maxval,cv2.THRESH_BINARY)
# Otsu 阈值处理
otsu_threshold = 0
otsuThe,dst_Otsu = cv2.threshold(src,otsu_threshold, maxval,cv2.THRESH_OTSU)
print(otsuThe,dst_Otsu)
# TRIANGLE 阈值处理
tri_threshold = 0
triThe,dst_tri = cv2.threshold(src, tri_threshold, maxval, cv2.THRESH_TRIANGLE)
print(triThe,dst_tri)
'''
输出
98.0 # Otsu 自动计算的阈值
[[255 255 0]
[ 0 0 0]
[ 0 0 255]
[255 0 0]
[ 0 255 255]]
232.0 # Triangle自动计算的阈值
[[ 0 255 0]
[ 0 0 0]
[ 0 0 255]
[ 0 0 0]
[ 0 0 0]]
'''
C++ 示例
#include直方图技术法
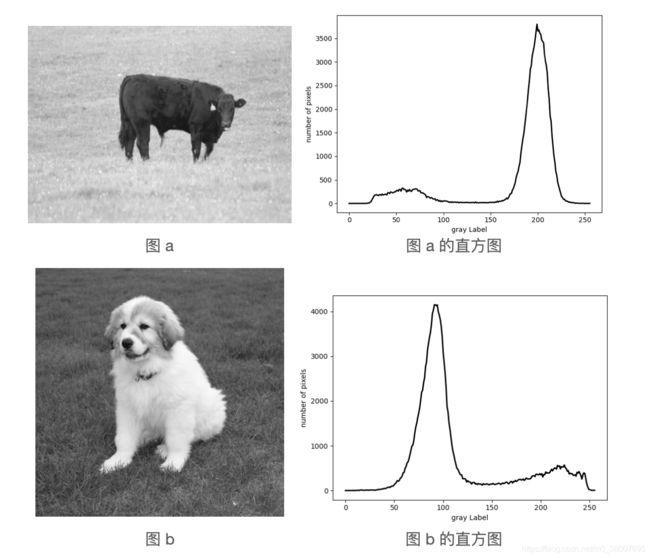
一幅含有一个与背景呈现明显对比的物体的图像具有包含双峰的直方图。如下图所示:
两个峰值对应物体内部和外部较多数目的点,两个峰值之间的波谷对应于物体边缘附近相对较少数目的点。直方图技术法就是先找到这两个峰值,然后取两个峰值之间的波谷对应的灰度值,就是所要的阈值。由于灰度值在直方图中的随机波动,两个波峰(局部最大值)和它们之间的波谷都不能很好的确定,比如在两个峰值之间可能会出现两个最小值,所以希望通过鲁棒的方法选定与最小值对应的阈值。一种常用的方法是先对直方图进行高斯平滑处理,逐渐增大高斯滤波器的标准差,直到能从平滑后的直方图中得到两个唯一的波峰和它们之间唯一的最小值。但这种方式需要手动调节,下面介绍一种规则自动选取波峰和波谷的方式。
假设输入图像为 I I I,高度为 H H H,宽为 W W W, histogram I \text{histogram}_I histogramI 代表其对应的灰度直方图, histogram I ( k ) \text{histogram}_I(k) histogramI(k) 代表灰度值等于 k k k 的像素点个数,其中 0 ≤ k ≤ 255 0\leq k \leq 255 0≤k≤255
-
找到灰度直方图的第一个峰值,并找到其对应的灰度值。显然,灰度直方图的最大值就是第一个峰值且对应的灰度值用 firstPeak 表示。
-
找到直方图的第二个峰值,并找到其对应的灰度值。第二个峰值不一定是直方图的第二大值,因为它很有可能出现在第一个峰值的附近。可以通过以下公式进行计算
secondPeak = arg k max { ( k − firstPeak ) 2 ∗ histogram I ( k ) } , 0 ≤ k ≤ 255 \text{secondPeak} = \text{arg}_k\text{max}\{(k - \text{firstPeak})^2 * \text{histogram}_{I}(k)\}, 0\leq k \leq 255 secondPeak=argkmax{(k−firstPeak)2∗histogramI(k)},0≤k≤255
也可以使用绝对值的形式:
secondPeak = arg k max { ∣ k − firstPeak ∣ ∗ histogram I ( k ) } , 0 ≤ k ≤ 255 \text{secondPeak} = \text{arg}_k\text{max}\{|k - \text{firstPeak}| * \text{histogram}_{I}(k)\}, 0\leq k \leq 255 secondPeak=argkmax{∣k−firstPeak∣∗histogramI(k)},0≤k≤255 -
找到这两个峰值之间的波谷,如果出现两个或者多个波谷,则取左侧的波谷即可,其对应的灰度值即为阈值
Python 示例
def threshold_two_peak(image):
# 计算灰度直方图
histogram = calcGrayHist(image)
# 找到灰度直方图的最大峰值对应的灰度值
maxLoc = np.where(histogram==np.max(histogram))
firstPeak = maxLoc[0][0]
# 寻找灰度直方图的第二个峰值对应的灰度值
measureDists = np.zeros([256], np.float32)
for k in range(256):
measureDists[k] = pow(k-firstPeak, 2) * histogram[k]
maxLoc2 = np.where(measureDists==np.max(measureDists))
secondPeak = maxLoc2[0][0]
# 找到两个峰值之间的最小值对应的灰度值,作为阈值
thresh = 0
if firstPeak > secondPeak: # 第一个峰值在第二个峰值的右侧
temp = histogram[int(secondPeak):int(firstPeak)]
minLoc = np.where(temp==np.min(temp))
thresh = secondPeak + minLoc[0][0] + 1
else: # 第一个峰值在第二个峰值的右侧
temp = histogram[int(firstPeak):int(secondPeak)]
minLoc = np.where(temp==np.min(temp))
thresh = firstPeak + minLoc[0][0] + 1
# 找到阈值后进行阈值处理,得到二值图
threshImage = image.copy()
threshImage[threshImage>thresh] = 255
threshImage[threshImage<=thresh] = 0
print(firstPeak, secondPeak, thresh)
return thresh, threshImage
def calcGrayHist(I):
# 计算灰度直方图
h, w = I.shape[:2]
grayHist = np.zeros([256], np.uint64)
for i in range(h):
for j in range(w):
grayHist[I[i][j]] += 1
return grayHist
C++ 示例
#include可得到图a与图b阈值分割后的图像
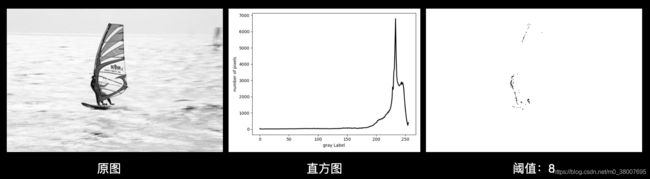
采用直方图技术对灰度直方图有两个明显波峰的图像的阈值处理效果比较好,而大多数图像的灰度直方图不会出现明显的两个峰值,如下图所示,由直方图技术法获得的第一峰值为233,第二峰值为0,阈值为8分割出的图像并不理想,没有比较完整的分割出前景和背景,几乎分辨不清目标物体。
熵算法
信息熵(entropy)的概念来源于信息论,假设信源符号 u u u 有 N N N 种取值,记为
u 1 , u 2 , ⋯ , u N u_1, u_2, \cdots, u_N u1,u2,⋯,uN
且每一种信源出现的概率,记为
p 1 , p 2 , ⋅ , p N p_1, p_2, \cdot, p_N p1,p2,⋅,pN
那么该信源符号的信息熵记为
entropy ( u ) = − ∑ i = 1 N p i log p i \text{entropy}(u) = - \sum_{i=1}^N p_i \log p_i entropy(u)=−i=1∑Npilogpi
图像也可以看作一种信源,把信息熵的概念带入图像就是,图像的信息熵越大(信息量大),所包含的细节越多,图像就越清晰。假设输入图像为 I I I, normHist I \text{normHist}_I normHistI 代表归一化的图像灰度直方图,那么对于 8 位图可以看成由 256 个灰度符号,且每一个符号出现的概率为 normHist I ( k ) \text{normHist}_I(k) normHistI(k) 组成的信源,其中 0 ≤ k ≤ 255 0 \leq k \leq 255 0≤k≤255
利用熵计算阈值的步骤如下
-
计算 I I I 的累加概率直方图,又称零阶累积矩,记为
cumuHist ( k ) = ∑ i = 0 k normHist I ( i ) , k ∈ [ 0 , 255 ] \text{cumuHist}(k) = \sum_{i=0}^{k} \text{normHist}_I(i), k\in[0,255] cumuHist(k)=i=0∑knormHistI(i),k∈[0,255] -
计算各个灰度级的熵,记为
entropy ( t ) = − ∑ k = 0 t normHist I ( k ) log ( normHist I ( k ) ) , 0 ≤ k ≤ 255 \text{entropy}(t) = - \sum_{k=0}^t \text{normHist}_I(k)\log(\text{normHist}_I(k)), 0 \leq k \leq 255 entropy(t)=−k=0∑tnormHistI(k)log(normHistI(k)),0≤k≤255 -
计算使 f ( t ) = f 1 ( t ) + f 2 ( t ) f(t) = f_1(t) + f_2(t) f(t)=f1(t)+f2(t) 最大化的 t 值,该值即为得到的阈值,即 thresh = arg t max ( f ( t ) ) \text{thresh} = \text{arg}_t \text{max}(f(t)) thresh=argtmax(f(t))
f 1 ( t ) = entropy ( t ) entropy ( 255 ) log ( cumuHist ( t ) ) log ( max { cumuHist ( 0 ) , cumuHist ( 1 ) , ⋯ , cumuHist ( t ) } ) f_1(t) = \frac{\text{entropy}(t)}{\text{entropy}(255)} \frac{\log(\text{cumuHist}(t))}{\log(\max\{\text{cumuHist}(0),\text{cumuHist}(1), \cdots, \text{cumuHist}(t)\})} f1(t)=entropy(255)entropy(t)log(max{cumuHist(0),cumuHist(1),⋯,cumuHist(t)})log(cumuHist(t))f 1 ( t ) = ( 1 − entropy ( t ) entropy ( 255 ) ) log ( 1 − cumuHist ( t ) ) log ( max { cumuHist ( t + 1 ) , ⋯ , cumuHist ( 255 ) } ) f_1(t) = (1- \frac{\text{entropy}(t)}{\text{entropy}(255)} )\frac{\log(1- \text{cumuHist}(t))}{\log(\max\{\text{cumuHist}(t+1), \cdots, \text{cumuHist}(255)\})} f1(t)=(1−entropy(255)entropy(t))log(max{cumuHist(t+1),⋯,cumuHist(255)})log(1−cumuHist(t))
Python 示例
import math
import cv2
import numpy as np
def calcGrayHist(image):
rows, cols = image.shape[:2]
grayHist = np.zeros([256], np.uint64)
for row in range(rows):
for col in range(cols):
grayHist[image[row][col]] += 1
return grayHist
def thresh_entropy(image):
rows, cols = image.shape
# 求灰度直方图
grayHist = calcGrayHist(image)
# 归一化灰度直方图,即概率直方图
normGrayHist = grayHist / float(rows*cols)
# 1.计算累加直方图
zeroCumuMoment = np.zeros([256], np.float32)
for i in range(256):
if i == 0:
zeroCumuMoment[i] = normGrayHist[i]
else:
zeroCumuMoment[i] = zeroCumuMoment[i-1] + normGrayHist[i]
# 2.计算各个灰度级的熵
entropy = np.zeros([256], np.float32)
for i in range(256):
if i == 0:
if normGrayHist[i] == 0:
entropy[i] = 0
else:
entropy[i] = -normGrayHist[i] * math.log10(normGrayHist[i])
else:
if normGrayHist[i] == 0:
entropy[i] = entropy[i-1]
else:
entropy[i] = entropy[i-1] - normGrayHist[i] * math.log10(normGrayHist[i])
# 3.找阈值
fT = np.zeros([256], np.float32)
ft1, ft2 = 0, 0
totalEntropy = entropy[255]
for i in range(255):
# 找最大值
maxFront = np.max(normGrayHist[0:i+1])
maxBack = np.max(normGrayHist[i+1:256])
if maxFront == 0 or zeroCumuMoment[i] == 0 or maxFront == 1 or zeroCumuMoment[i] == 1 or totalEntropy == 0:
ft1 = 0
else:
ft1 = entropy[i] / totalEntropy * (math.log10(zeroCumuMoment[i]) / math.log10(maxFront))
if maxBack == 0 or 1-zeroCumuMoment[i] == 0 or maxBack == 1 or 1-zeroCumuMoment[i] == 1:
ft2 = 0
else:
if totalEntropy == 0:
ft2 = (math.log10(1-zeroCumuMoment[i])/math.log10(maxBack))
else:
ft2 = (1-entropy[i] / totalEntropy)*(math.log10(1-zeroCumuMoment[i])/math.log10(maxBack))
fT[i] = ft1 + ft2
# 找最大值的索引,作为得到的阈值
threshLoc = np.where(fT==np.max(fT))
thresh = threshLoc[0][0]
# 阈值处理
threshold = np.copy(image)
threshold[threshold>thresh] = 255
threshold[threshold<=thresh] = 0
return thresh, threshold
if __name__ == '__main__':
img = cv2.imread("./images/img8.jpg", 0)
thresh, threshImg = thresh_entropy(img)
cv2.imwrite('./images/img8_entropy.jpg', threshImg)
cv2.imshow('thresh', threshImg)
cv2.waitKey()
效果
从图中可以看出,所得到的效果并没有比采用直方图技术进行阈值分割得到的效果有明显的提升,所以针对阈值分选取什么样的方法,需要分情况对待。
Otsu算法
在对图像进行阈值分割时,所选取的分割阈值应使前景区域的平均灰度、背景区域的平均灰度与整幅图像的平均灰度之间的差值最大,这种差异用区域的方差来表示。Otsu提出了最大方差法,该算法是在判别分析最小二乘法原理的基础上推导得到的,计算过程简单,是一种常用的阈值分割的稳定算法。
原理详解
Otsu计算出的阈值是使前景区域的平均灰度、背景区域的平均灰度与整幅图像的平均灰度之间的差值最大,即最大类间方差法。
假设有阈值 thresh 把图像中的所有像素分为两部分,这两部分的像素均值分别为 m l , m r m_l, m_r ml,mr ,图像的总体均值为 m g m_g mg,这两部分的像素的概率(即像素个数占总像素个数的比例)为 p l , p r p_l, p_r pl,pr,可知 m g = p l ∗ m l + p r ∗ m r , p l + p r = 1 m_g = p_l * m_l + p_r*m_r, \; \; p_l + p_r = 1 mg=pl∗ml+pr∗mr,pl+pr=1,类间方差可表示为
σ 2 = p l ∗ ( m l − m g ) 2 + p r ∗ ( m r − m g ) 2 (1) \sigma^2 = p_l* (m_l - m_g)^2 + p_r *(m_r - m_g)^2 \tag{1} σ2=pl∗(ml−mg)2+pr∗(mr−mg)2(1)
化简可得
σ 2 = p l p r ( m l − m r ) 2 (2) \sigma^2 = p_l p_r (m_l-m_r)^2 \tag{2} σ2=plpr(ml−mr)2(2)
此时就可以求出使 σ 2 \sigma^2 σ2 最大对应的灰度值 k 便是 Otsu 阈值。可以根据这个方法计算,也可以根据下边的方法计算。其中
m l = 1 p l ∑ i = 0 k i p i m r = 1 p r ∑ i = k + 1 255 i p i (3) \begin{aligned} & m_l = \frac{1}{p_l} \sum_{i=0}^k i p_i \\ & m_r = \frac{1}{p_r} \sum_{i=k+1}^{255} ip_i \end{aligned} \tag{3} ml=pl1i=0∑kipimr=pr1i=k+1∑255ipi(3)
又因为 k 的一阶累积矩(均值的累加) m m m 和总体均值 m g m_g mg 为
m = ∑ i = 0 k i p i m g = ∑ i = 0 255 i p i (4) \begin{aligned} & m = \sum_{i=0}^k ip_i \\ & m_g = \sum_{i=0}^{255} ip_i \end{aligned} \tag{4} m=i=0∑kipimg=i=0∑255ipi(4)
根据公式 (3) 和 (4) 可得
m l = 1 p l m m r = 1 p r ( m g − m ) (5) \begin{aligned} & m_l = \frac{1}{p_l} m \\ & m_r = \frac{1}{p_r} (m_g-m) \end{aligned} \tag{5} ml=pl1mmr=pr1(mg−m)(5)
将公式 (5) 代入到 (2) 中可得
σ 2 = ( m g ∗ p l − m ) 2 p l ∗ ( 1 − p l ) \sigma^2 = \frac{(m_g * p_l - m)^2}{p_l * (1-p_l)} σ2=pl∗(1−pl)(mg∗pl−m)2
这时就可以根据 k 的零阶累积矩 p l p_l pl 、一阶累积矩 m m m 和图像的总体均值 m g m_g mg 来计算 σ 2 \sigma^2 σ2 ,求出使得 σ 2 \sigma^2 σ2 最大的 k 记为分割阈值。
计算步骤
假设输入图像为 I I I,高度为 H H H,宽为 W W W, histogram I \text{histogram}_I histogramI 代表归一化的灰度直方图, histogram I ( k ) \text{histogram}_I(k) histogramI(k) 代表灰度值等于 k k k 的像素点在图像中所占的比率,其中 0 ≤ k ≤ 255 0\leq k \leq 255 0≤k≤255 。详细步骤如下
-
计算灰度直方图的零阶累积矩(或称累加直方图)
zeroCumuMoment ( k ) = ∑ i = 1 k histogram I ( i ) , k ∈ [ 0 , 255 ] \text{zeroCumuMoment}(k) = \sum_{i=1}^k \text{histogram}_I(i), k\in[0,255] zeroCumuMoment(k)=i=1∑khistogramI(i),k∈[0,255] -
计算灰度直方图的一阶累积矩
oneCumuMoment ( k ) = ∑ i = 1 k ( i ∗ histogram I ( i ) ) , k ∈ [ 0 , 255 ] \text{oneCumuMoment}(k) = \sum_{i=1}^k(i*\text{histogram}_I(i)), k\in[0,255] oneCumuMoment(k)=i=1∑k(i∗histogramI(i)),k∈[0,255] -
计算图像 I I I 总体的灰度平均值 mean,其实就是 k = 255 k=255 k=255 时的一阶累积矩,即
mean = oneCumuMoment ( 255 ) \text{mean} = \text{oneCumuMoment}(255) mean=oneCumuMoment(255) -
计算每一个灰度级作为阈值时,前景区域的平均灰度、背景区域的平均灰度与整幅图像的平均灰度的方差。对方差的衡量采用以下度量:
σ 2 ( k ) = ( mean ∗ zeroCumuMoment ( k ) − oneCumuMoment ( k ) ) 2 zeroCumuMoment ( k ) ∗ ( 1 − zeroCumuMoment ( k ) ) , k ∈ [ 0 , 255 ] \sigma^2(k) = \frac{(\text{mean} * \text{zeroCumuMoment}(k) - \text{oneCumuMoment}(k))^2}{\text{zeroCumuMoment}(k) * (1-\text{zeroCumuMoment}(k))}, k\in[0,255] σ2(k)=zeroCumuMoment(k)∗(1−zeroCumuMoment(k))(mean∗zeroCumuMoment(k)−oneCumuMoment(k))2,k∈[0,255] -
找到 σ 2 ( k ) \sigma^2(k) σ2(k) ,然后对应的 k k k 即为 Otsu 自动选取的阈值,即
thresh = arg k ∈ [ 0 , 255 ) max ( σ 2 ( k ) ) \text{thresh} = \arg_{k\in[0,255)} \max(\sigma^2(k)) thresh=argk∈[0,255)max(σ2(k))
Python 实现
import math
import cv2
import numpy as np
def calc_gray_hist(image):
rows, cols = image.shape[:2]
gray_hist = np.zeros([256], np.uint64)
for i in range(rows):
for j in range(cols):
gray_hist[image[i][j]] += 1
return gray_hist
def otsu_thresh(image):
rows, cols = image.shape[:2]
# 计算灰度直方图
gray_hist = calc_gray_hist(image)
# 归一化灰度直方图
norm_hist = gray_hist / float(rows*cols)
# 计算零阶累积矩, 一阶累积矩
zero_cumu_moment = np.zeros([256], np.float32)
one_cumu_moment = np.zeros([256], np.float32)
for i in range(256):
if i == 0:
zero_cumu_moment[i] = norm_hist[i]
one_cumu_moment[i] = 0
else:
zero_cumu_moment[i] = zero_cumu_moment[i-1] + norm_hist[i]
one_cumu_moment[i] = one_cumu_moment[i - 1] + i * norm_hist[i]
# 计算方差,找到最大的方差对应的阈值
mean = one_cumu_moment[255]
thresh = 0
sigma = 0
for i in range(256):
if zero_cumu_moment[i] == 0 or zero_cumu_moment[i] == 1:
sigma_tmp = 0
else:
sigma_tmp = math.pow(mean*zero_cumu_moment[i] - one_cumu_moment[i], 2) / (zero_cumu_moment[i] * (1.0-zero_cumu_moment[i]))
if sigma < sigma_tmp:
thresh = i
sigma = sigma_tmp
# 阈值分割
thresh_img = image.copy()
thresh_img[thresh_img>thresh] = 255
thresh_img[thresh_img<=thresh] = 0
return thresh, thresh_img
if __name__ == '__main__':
image = cv2.imread('./images/img7.jpg', 0)
thresh, thresh_img = otsu_thresh(image)
print(thresh)
cv2.imwrite('./images/img7_otsu.jpg', thresh_img)
cv2.imshow('thresh', thresh_img)
cv2.waitKey()
C++ 实现
方法一:
int myOstu(Mat grayImg, Mat& binImg) {
int rows = grayImg.rows;
int cols = grayImg.cols;
int sumPix = rows * cols;
// 灰度直方图
vector<int> grayHist;
for (int i = 0; i < 256; i++)
{
grayHist.push_back(0);
}
for(int r = 0; r < rows; r++)
{
for(int c = 0; c < cols; c++)
{
int gray = grayImg.at<uchar>(r, c);
grayHist[gray]++;
}
}
float sum = 0;
for(int i = 0; i < 256; i++)
{
sum += i * grayHist[i];
}
float sumB = 0;
int wB = 0;
int wF = 0;
float varMax = 0;
int thresh = 0;
for (int i = 0; i < 256; i++)
{
wB += grayHist[i]; // 背景权重
if(wB == 0)
{
continue;
}
wF = sumPix - wB; // 前景权重
if(wF == 0)
{
break;
}
sumB += (float)(i * grayHist[i]);
float mB = sumB / wB; // 背景均值
float mF = (sum - sumB) / wF; //前景均值
float varTmp = (float)wB/(float)sumPix * (float)wF/(float)sumPix * (mB - mF) * (mB - mF); // 计算方差
if(varTmp > varMax)
{
varMax = varTmp;
thresh = i;
}
}
// 阈值处理
threshold(grayImg, binImg, thresh, 255, THRESH_BINARY);
return thresh;
}
方法二:
#include效果
上图为 otsu 阈值分割后的效果,可以看出,所得到的效果比采用直方图和熵阈值法得到的效果要好,均比较完整地分割了前景和背景,能够分辨图中的目标物体。
2. 局部阈值分割
在比较理想的情况下,对整个图像使用单个阈值进行阈值化才会成功。而在许多情况下,如受光照不均等因素影响,全局阈值分割往往效果不是很理想,在这种情况下,使用局部阈值(又称自适应阈值)进行分割可以产生好的结果。
局部阈值分割不像全局阈值那样,对整个矩阵采用一个阈值,而是针对输入矩阵的每一个位置的值都有相对应的阈值。
自适应阈值
在不均匀照明或者灰度值分布不均匀的情况下,如果使用全局阈值分割,那么得到的分割效果往往会很不理想,如处理光照不均匀的两幅图,效果如下图所示,显示结果只是将光照较强的区域分割出来了,而阴影部分或者光照较弱的区域却没有分割出来。
原理详解
在自适应阈值处理中,平滑算子的尺寸矩定了分割出来的物体的尺寸,如果滤波器尺寸太小,那么估计出的局部阈值将不理想。凭经验,平滑算子的宽度必须大于被识别物体的宽度,窗口的尺寸越大,平滑后结果越能更好地作为每个像素的阈值的参考,当然也不能无限大。
假设输入图像为 I I I,高度为 H H H,宽为 W W W,自适应阈值分割算法的步骤如下
-
对图像进行平滑处理,平滑结果记为 f s m o o t h ( I ) f_{smooth}(I) fsmooth(I),其中 f s m o o t h f_{smooth} fsmooth 可以代替均值平滑、高斯平滑、中值平滑
-
自适应阈值矩阵 Thresh = ( 1 − ratio ) ∗ f s m o o t h ( I ) \text{Thresh} = (1-\text{ratio}) * f_{smooth}(I) Thresh=(1−ratio)∗fsmooth(I),一般令 ratio = 0.15
-
利用局部阈值分割规则
O ( r , c ) = { 255 I ( r , c ) > Thresh ( r , c ) 0 I ( r , c ) ≤ Thresh ( r , c ) O(r,c) = \begin{cases} 255 & I(r,c) > \text{Thresh}(r,c) \\ 0 & I(r,c) \leq \text{Thresh}(r,c) \end{cases} O(r,c)={2550I(r,c)>Thresh(r,c)I(r,c)≤Thresh(r,c)
Python 实现
import cv2
import numpy as np
# 使用均值平滑
def adaptive_thresh(image, win_size, ratio=0.15):
# 对图像矩阵进行均值平滑
image_mean = cv2.blur(image, win_size)
# 原图像矩阵与平滑结果做差
out = image - (1.0-ratio) * image_mean
# 当差值大于或等于0时,输出值为255,反之输出值为0
out[out >= 0] = 255
out[out < 0] = 0
out = out.astype(np.uint8)
return out
if __name__ == '__main__':
img = cv2.imread("./images/image3.png", 0)
threshImg = adaptive_thresh(img, (3,3))
cv2.imwrite('./images/image3_adaptive.jpg', threshImg)
cv2.imshow('thresh', threshImg)
cv2.waitKey()
C++ 实现
#includeOpenCV 函数:
void cv::adaptiveThreshold ( InputArray src,
OutputArray dst,
double maxValue,
int adaptiveMethod,
int thresholdType,
int blockSize,
double C
)
| 参数 | 解释 |
|---|---|
| src | 源图像,单通道矩阵 |
| dst | 输出图像 |
| maxValue | 分配给满足条件的像素的非零值。 |
| adaptiveMethod | 自适应阈值算法:ADAPTIVE_THRESH_MEAN_C(均值平滑) 和 ADAPTIVE_THRESH_GAUSSIAN_C(高斯平滑) |
| thresholdType | 阈值类型,必须是THRESH_BINARY或THRESH_BINARY_INV。 |
| blockSize | 像素邻域的大小,用于计算像素的阈值。3、5、7等。 |
| C | 从平均数或加权平均数中减去的常数(见下文细节)。通常,它是正数,但也可能是零或负数。 |
- ADAPTIVE_THRESH_MEAN_C 阈值 T(x, y) 是像素 (x,y) 的邻域(3x3 或 5x5) 均值减去常量C
- ADAPTIVE_THRESH_GAUSSIAN_C 阈值 T(x, y) 是像素 (x,y) 的邻域(3x3 或 5x5) 加权和(Gaussian)减去常量C。默认 sigma(标准差) 用于指定块大小。
函数只是采用了均值平滑、高斯平滑,并没有采用中值平滑,在处理特定问题时,需要通过实验对比的方式,选择其中一种比较理想的平滑方式。对图像进行阈值分割之后仍然需要进一步的处理,形态学处理。