CUDA 编程模型

CUDA 编程模型

这部分将重点介绍 CUDA 编程模型的两个主要的抽象概念：内存层次结构和线程层次结构，它们能够控制大规模并行 GPU。

1 内存管理

一个异构环境，通常有多个 CPU 多个 GPU，每个 CPU 和 GPU 的内存都由一条 PCI-Express 总线分隔开。所以要区分以下内容：

• 主机：CPU及其内存(主机内存)
• 设备：GPU及其内存(设备内存)

为了规范化，在之后的代码中，主机内存中的变量名以 h_ 为前缀，设备内存中的变量名以 d_ 为前缀

一个典型的 CUDA 程序包括由并行代码互补的串行代码，如图所示，串行代码在主机 CPU 上执行，而并行代码在 GPU 上执行。

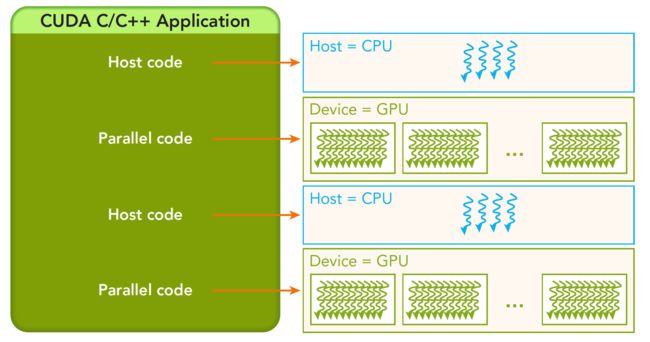
Host API 和 CUDA C 的 API 的对比：

ANSI C 函数	CUDA C 函数	说明
malloc	cudaMalloc	内存分配
memcpy	cudaMemcpy	内存复制
memset	cudaMemset	内存设置
free	cudaFree	释放内存

内存拷贝：

cudaError_t cudaMemcpy(void *dst, const void *src, size_t count, cudaMemcpyKind kind)

此函数用于 Host 和 Device 之间内存的拷贝，从 src 拷贝 count 大小字节的数据到 dst，方向由 kind 指定，kind 有以下几种：

• cudaMemcpyHostToHost
• cudaMemcpyHostToDevice
• cudaMemcpyDeviceToHost
• cudaMemcpyDeviceToDevice

2 线程管理

当核函数在 Host 启动时，它的执行会移动到 Device，此时，Device 上会产生大量的线程(thread)，并且每个 thread 都执行由核函数指定的语句。

由一个核函数启动所产生的的所有线程统称为一个网格(grid)，同一个 grid 中的 thread 共享 Global Memory，一个 grid 由多个线程块(block)组成，一个 block 中包含一组 thread，同一个 block 中的 thread 共享 Shared Memory。

同一个 block 内的 thread 可以完成以下协作：

• 同步
• 共享内存

不同 block 内的 thread 不能协作，因为它们之间有物理隔离。

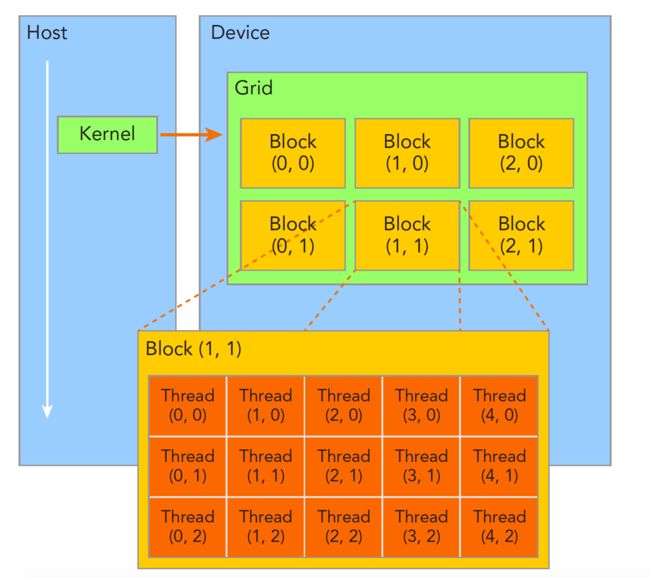
如何确定每个 thread 的索引?

每个 gird 中存在以下结构体用于确定 thread 索引：

• blockIdx(block 在 grid 内的位置索引)
  • blockIdx.x
  • blockIdx.y
  • blockIdx.z
• threadIdx(thread 在 block 内的位置索引)
  • threadIdx.x
  • threadIdx.y
  • threadIdx.z
• blockDim(block 的维度)
  • blockDim.x
  • blockDim.y
  • blockDim.z
• gridDim(grid 的维度)
  • gridDim.x
  • gridDim.y
  • gridDim.z

图中 Thread(2, 1) 的各项值为：

threadIdx.x = 2, threadIdx.y = 1, threadIdx.z = 0;

blockIdx.x = 1, blockIdx.y = 1, blockIdx.z = 0;

blockDim = (5, 3, 1)

gridDim = (3, 2, 1)

其在整个 grid 中的索引为：$ix=blockIdx.x\ast blockDim.x+threadIdx.x$，$iy=blockIdx.y\ast blockDim.y+threadIdx.y$

对于一个给定的数据大小，确定 gridDim 和 blockDim 的一般步骤为：

• 确定 blockDim
• 在一直数据大小和 blockDim 的基础上计算 gridDim

要确定 blockDim，通常需要考虑：

• 核函数的性能特性
• GPU 资源的限制

下面代码使用一维 grid 和 一维 block 来说明 block 和 grid 的关系，其中数据大小是固定的。

// defineGridBlock.cu
#include 
#include 
int main(int argc, char** argv)
{
	int nElem = 1024;
	dim3 block(1024);
	dim3 grid((nElem - 1) / block.x + 1);
	printf("grid.x %d block.x %d\n", grid.x, block.x);

	block.x = 512;
	grid.x = (nElem - 1) / block.x + 1;
	printf("grid.x %d block.x %d\n", grid.x, block.x);

	block.x = 256;
	grid.x = (nElem - 1) / block.x + 1;
	printf("grid.x %d block.x %d\n", grid.x, block.x);

	block.x = 128;
	grid.x = (nElem - 1) / block.x + 1;
	printf("grid.x %d block.x %d\n", grid.x, block.x);

	cudaDeviceReset();
	return 0;
}

3 CUDA 核函数

启动一个 CUDA 核函数

在代码添加如下代码即可启动编写好的核函数

kernel_name<<<grid, block>>>(parameters);

假设有 32 个数据元素用于计算，每 8 个元素一个 block，则需要 4 个 block：

kernel_name<<<4, 8>>>(parameters);

由于 CUDA C 核函数的启动都是异步的，因此在启动核函数之后需要添加 cudaDeviceSynchronize() 用于显式的同步。

编写核函数

核函数是在设备上运行的代码。在核函数中，需要为一个线程规定要进行的计算以及要进行的数据访问。前文所述，当一个核函数启动时，会启动一个 grid，grid 中的所有 thread 并行执行同一个计算任务。使用 __global__ 声明、定义核函数：

__global__ void kernel_name(parameters);

CUDA 核函数的限制

• 只能访问设备内存
• 必须具有 void 返回类型
• 不支持可变数量的参数
• 不支持静态变量
• 显示异步行为

举一个向量加法的例子：将两个大小为 $N$ 的向量 $\mathbf{A}$ 和向量 $\mathbf{B}$ 相加。

串行代码：

void sumVectorOnHost(float *A, float *B, float *C, const int N)
{
    for (int i = 0; i < N; i ++)
        C[i] = A[i] + B[i];
}

并行代码：

__global__ void sumVectorOnDevice(float *A, float *B, float *C, const int N)
{
    int i = threadIdx.x;//计算线程编号
    C[i] = A[i] + B[i];
}

4 CUDA 线程组织结构

这一部分会介绍在不同的线程组织结构中，如何确定线程的唯一索引，然后进行并行计算，并且不同的线程组织形式的性能不同：

• 由二维 block 构成的二维 grid
• 由一维 block 构成的一维 grid
• 由一维 block 构成的二维 grid

4.1 使用块和线程建立矩阵索引

一个矩阵通常采用行优先的方法线性存放在全局内存中。对于一个 8x6 的矩阵，其在内存中的存放方式如图所示：

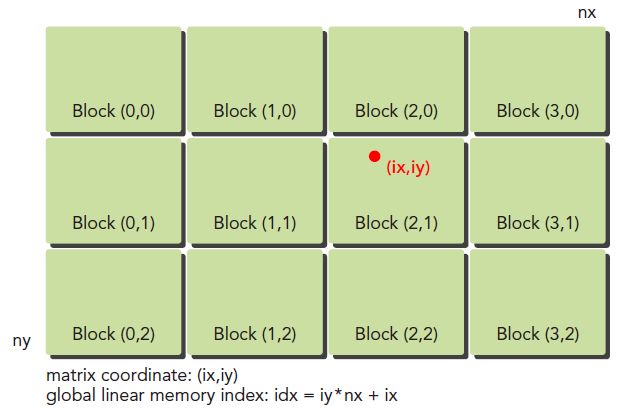
对于下图所示由二维 block 构成的二维 grid 线程组织结构，其中任意一个 thread 的坐标(ix, iy)可以通过式子(1)计算出来。
$$\begin{gathered} ix=blockIdx.x\ast blockDim.x+threadIdx.x \\ iy=blockIdx.y\ast blockDim.y+threadIdx.y\text{\hspace{1em}(1)} \end{gathered}$$
那么对于坐标为(ix, iy)的 thread，其在内存中对应的线性索引为：$idx=iy\ast nx+ix$，其中 $nx=blockIdx.x\ast gridDim.x$

上面已经计算出了每个 thread 的全局坐标(ix, iy)，用坐标为(ix, iy)的 thread 对应矩阵中坐标为(ix, iy)元素，这样就形成了一一对应，如使用坐标为(5, 5)的 thread 对应坐标为(5, 5)的元素。这样在做矩阵加法的时候，直接使用 idx 取得对应位置的元素做加法即可，如下面的核函数所示：

__global__ void MatrixSum(float *A, float *B, float *C, int nx, int ny)
{
    int ix = blockIdx.x * blockDim.x + threadIdx.x;
    int iy = blockIdx.y * blockDim.y + threadIdx.y;
    int idx = nx * iy + ix;
    if (ix < nx && iy < ny)
        C[idx] = A[idx] + B[idx];
}

4.2 使用二维 grid 和二维 block 对矩阵求和

定义核函数

__global__ void MatrixSum22(float *A, float *B, float *C, int nx, int ny)
{
    int ix = blockIdx.x * blockDim.x + threadIdx.x;
    int iy = blockIdx.y * blockDim.x + threadIdx.y;
    int idx = iy * nx + ix;
    if (ix < nx && iy < ny)
        C[idx] = A[idx] + B[idx];
}

线程配置

int nx = 1 << 14;//定义矩阵
int ny = 1 << 14;//定义矩阵
int dimx = 32;
int dimy = 32;
dim3 block(dimx, dimy);
dim3 grid((nx - 1) / block.x + 1, (ny - 1) / block.y + 1);
MatrixSum22<<<grid, block>>>(A, B, C, nx, ny);

4.3 使用一维 grid 和一维 block 对矩阵求和

在该结构中，每一个 block 中只有一个 thread，每一个 thread 需要计算矩阵的一列元素。

定义核函数

__global__ void MatrixSum11(float *A, float *B, float *C, int nx, int ny)
{
    int ix = blockIdx.x * blockDim.x + threadIdx.x;
    if (ix < nx)
    {
        for (int iy = 0; iy < ny; iy ++)
        {
            int idx = iy * nx + ix;
            C[idx] = A[idx] + B[idx];
        }
    }
}

线程配置

int nx = 1 << 14;
int ny = 1 << 14;
int dimx = 32;
int dimy = 1;
dim3 block(dimx, dimy);
dim3 grid((nx - 1) / block.x + 1, 1);
MatrixSum11<<<grid, block>>>(A, B, C, nx, ny);

4.4 使用二维 grid 和一维 block 对矩阵求和

当使用一个包含一维 block 的二维 grid 时，每个 thread 都只关注一个数据元素并且 grid 的第二个维数等于 ny。

定义核函数

__global__ void MatrixSum21(float *A, float *B, float *C, int nx, int ny)
{
    int ix = blockIdx.x * blockDim.x + threadIdx.x;
    int iy = blockIdx.y;
    int idx = iy * nx + ix;
    if (ix < nx && iy < ny)
        C[idx] = A[idx] + B[idx];
}

线程配置

int nx = 1 << 14;
int ny = 1 << 14;
int dimx = 32;
dim3 block(dimx);//缺省为1
dim3 grid((nx - 1) / block.x + 1, ny);
MatrixSum21<<<grid, block>>>(A, B, C, nx, ny);

从上面的矩阵加法的例子可以看出：

• 改变执行配置对核函数性能有影响
• 传统的核函数实现一般不能获得最佳性能
• 对于一个给定的核函数，尝试使用不同的 grid 和 block 大小可以获得更好的性能