在线学习(online learning)——Chapter 1 What is online learning
在线学习(online learning)——Chapter 1 What is online learning
引用
[1]Hoi S C H, Sahoo D, Lu J, et al. Online learning: A comprehensive survey[J]. Neurocomputing, 2021, 459: 249-289.点击阅读
[2]Orabona F. A modern introduction to online learning[J]. arXiv preprint arXiv:1912.13213, 2019.点击阅读
1 Introduction
机器学习在现代数据分析和人工智能 (AI) 应用程序中发挥着至关重要的作用。传统的机器学习范式(paradigm)通常以批处理学习(batch learning)或离线学习(offline learning)的方式工作(尤其是对于监督学习),其中模型是通过某种学习算法从整个训练数据集中立即训练的,然后部署模型进行推理而不需要(或很少)之后执行任何更新。这种学习方法在处理新的训练数据时会产生昂贵的再训练成本,因此在实际应用中的可扩展性很差。
与传统的机器学习不同,在线学习是机器学习的一个子领域,它被设计成以连续的方式从数据中渐进地学习模型。在线学习克服了传统批量学习的缺点,当新的训练数据到来时,模型可以被在线学习者即时有效地更新。
1.1 What is Online Learning?
传统的机器学习范式通常以批学习方式运行,例如,监督学习任务,其中预先给出训练数据的集合,以通过遵循某种学习算法来训练模型。这种范例要求在学习任务之前提供整个训练数据集,并且由于昂贵的训练成本,训练过程通常在离线环境中进行。存在一些关键缺点:
- 时间和空间成本效率低
- 大规模应用程序的可扩展性较差,因为模型经常需要从头开始重新训练以获得新的训练数据
与批量学习算法不同,在线学习是一种机器学习方法,用于对按顺序到达的数据进行学习,学习者的目标是在每一步学习并更新未来数据的最佳预测值。在线学习能够克服批量学习的缺点,因为可以针对任何新的数据实例立即更新预测模型。因此,在线学习算法对于真实世界数据分析应用中的大规模机器学习任务更为有效和可扩展,在这些应用中,数据不仅规模大,而且速度快。
1.2 Tasks and Applications
在线学习技术可以应用于解决各种现实应用领域中的各种任务。应用场景示例如下:
Supervised learning tasks
可以为监督学习使用在线学习算法。最常见的任务之一是分类,旨在根据观察过去的训练数据实例(其类别标签已给出),预测新数据实例所属的类别。例如,在线学习中通常研究的任务是在线二分类(例如,垃圾邮件过滤),它只涉及两个类别(“垃圾邮件”和“良性”电子邮件);其他类型的监督分类任务包括多类分类、多标签分类和多实例分类等。
除了分类任务之外,另一个常见的监督学习任务是回归分析,这是指用于估计变量之间的关系(通常在因变量和一个或多个自变量之间)的学习过程。在线学习技术自然也可以应用于回归分析任务,例如金融市场中的时间序列分析,其中数据实例以顺序方式到达。此外,利用金融时间序列数据进行在线学习的另一个应用是在线投资组合分,在线学习者的目标是找到一个好的(例如,盈利和低风险)策略,以做出一系列投资组合选择决策。
Bandit learning tasks
Bandit在线学习算法,也称为Multi-armed bandits(MAB),已被广泛用于许多在线推荐系统,例如用于互联网货币化的在线广告、电子商务中的产品推荐、娱乐电影推荐和其他个性化推荐等。
Unsupervised learning tasks
在线学习算法可以应用于无监督的学习任务。这方面的例子包括聚类或聚类分析,使同一组(“聚类”)对象比其他聚类的对象更相似。在线聚类的目的是对一连串的实例进行增量聚类分析,这在挖掘数据流时很常见。
Other learning tasks
在线学习也可用于其他种类的机器学习任务,如推荐系统的学习、学习排名或强化学习。例如,在线学习的协同过滤可以应用于提高推荐系统的性能,通过学习从用户的连续评级/反馈信息流中依次改善协同过滤的任务。
协同过滤简单来说是利用某兴趣相投、拥有共同经验之群体的喜好来推荐用户感兴趣的信息,个人通过合作的机制给予信息相当程度的回应(如评分)并记录下来以达到过滤的目的进而帮助别人筛选信息,回应不一定局限于特别感兴趣的,特别不感兴趣信息的纪录也相当重要。
协同过滤又可分为评比(rating)或者群体过滤(social filtering)协同过滤以其出色的速度和健壮性,在全球互联网领域炙手可热。
在线学习技术通常用于两种主要场景。
- 一个是提高用于批处理机器学习任务的现有机器学习方法的效率和可扩展性,其中必须在学习任务之前提供完整的训练数据集合。例如,支持向量机(SVM)是用于批量分类任务的一种众所周知的监督学习方法,其中经典的SVM算法对于非常大规模的应用具有较差的可扩展性。
- 另一种情况是应用在线学习算法直接处理在线流数据分析任务,其中数据实例自然以顺序方式到达,而目标概念可能随时间漂移或演变。例子包括时间序列回归,如股票价格预测,其中数据定期到达,学习者必须在得到下一个实例之前立即做出决定。
1.3 Taxonomy
如图1所总结的。一般来说,从理论的角度来看,在线学习方法是建立在学习理论、优化理论和博弈理论这三大理论之上的。具体来说,根据学习任务中的反馈信息类型和监督类型,可以将在线学习技术分为以下三大类。
Online supervised learning
这涉及到受监督的学习任务,在每一轮在线学习结束时,总是向学习者透露完整的反馈信息。它可以进一步分为两组:
- “Online Supervised Learning”,形成了在线监督学习的基本方法和原则;
- “Applied Online Learning”,构成了更多的非传统的在线监督学习,其中的基本方法不能直接应用,算法已经被适当调整以适应非传统的在线学习环境。
Online learning with limited feedback
这涉及到在线学习者在在线学习过程中从环境中获得部分反馈信息的任务。例如,考虑一个在线多类分类任务,在某一回合,学习者对进入的实例进行类别标签的预测,然后收到部分反馈信息,表明预测是否正确,而不是明确的特定真实类别标签。对于这样的任务,在线学习者往往需要对 e x p l o r a t i o n − e x p l o i t a t i o n exploration-exploitation exploration−exploitation问题的权衡来做出在线更新或决定。
Online unsupervised learning
在线学习者在在线学习任务期间仅接收数据实例序列,而没有任何额外的反馈(例如,真实的班级标签)。无监督在线学习可以被认为是处理数据流的传统无监督学习的自然延伸。无监督的在线学习的示例包括在线聚类、在线降维和在线异常检测任务等。无监督的网络学习对数据的假设较少,不需要明确的反馈或标签信息,而这些信息可能很难或很难获取。
2 Case Description
用一个简单的例子来说明在线学习。
两个人重复以下游戏:
- 你的对手选择了一个数字 y t ∈ [ 0 , 1 ] y_t \in [0,1] yt∈[0,1],你不知道这个数字是多少。
- 你尝试去猜这个数字,选择了 x t ∈ [ 0 , 1 ] x_t \in [0,1] xt∈[0,1]。
- 对手公布这个数字,你需要付出平方差化的损失 ( x t − y t ) 2 (x_t-y_t)^2 (xt−yt)2。
我们想要尽可能精确地猜测一个数字序列。而要使比赛成立,必须决定什么是“获胜条件”。
首先,简化游戏。让我们假设对手抽到的数字独立同分布于[0,1]上的某个固定分布。如果我们知道分布,我们就可以预测每一轮分布的平均值,并在预期中付出 σ 2 T \sigma^2T σ2T的代价,其中 σ 2 σ^2 σ2是分布的方差。这就是最优情况!但是鉴于我们不知道分布情况,需要将我们的战略与最优战略进行比较。也就是要衡量如下标准:
E Y [ ∑ t = 1 T ( x t − Y ) 2 ] − σ 2 T \begin{equation} \mathbb E_Y\left[\sum_{t=1}^T (x_t - Y)^2\right] - \sigma^2 T\tag{1.1} \end{equation} EY[t=1∑T(xt−Y)2]−σ2T(1.1)
或者考虑平均值:
1 T E Y [ ∑ t = 1 T ( x t − Y ) 2 ] − σ 2 \begin{equation} \frac{1}{T}\mathbb E_Y\left[\sum_{t=1}^T (x_t - Y)^2\right] - \sigma^2\tag{1.2} \end{equation} T1EY[t=1∑T(xt−Y)2]−σ2(1.2)
如果(1.1)式中的差值随时间呈次线性增长,并且等价地,如果(1.2)式中的差值随轮数T趋于无穷大而趋于零,则认为策略"成功"是有意义的。也就是说,在平均轮数上,我们希望我们的算法能够接近最优性能。
2.1 最小化悔值(regret)
考虑到收敛成功。重写(1.1)如下:
E [ ∑ t = 1 T ( x t − Y ) 2 ] − min x ∈ [ 0 , 1 ] E [ ∑ t = 1 T ( x − Y ) 2 ] . \mathbb E\left[\sum_{t=1}^T (x_t - Y)^2\right] - \min_{ x \in [0,1]} \ \mathbb E\left[\sum_{t=1}^T (x-Y)^2\right]~. E[t=1∑T(xt−Y)2]−x∈[0,1]min E[t=1∑T(x−Y)2] .
当
Regret T : = ∑ t = 1 T ( x t − y t ) 2 − min x ∈ [ 0 , 1 ] ∑ t = 1 T ( x − y t ) 2 \text{Regret}_T:=\sum_{t=1}^T (x_t - y_t)^2 - \min_{x \in [0,1]} \ \sum_{t=1}^T (x - y_t)^2 RegretT:=t=1∑T(xt−yt)2−x∈[0,1]min t=1∑T(x−yt)2
随着T的增加而次线性增长,我们将会赢得比赛。悔值(Regret)可以从理论上评估在线学习算法的性能。
次线性(sublinear)增长是指 lim T → ∞ Regret T T \underset{T\to ∞}{\lim}{\frac{\text{Regret}_T}{T}} T→∞limTRegretT。次线性增长意味着算法的平均表现和最优决策的平均表现是相当的。
让我们进一步泛化该在线游戏:
- 算法输出一个向量 x t ∈ V ⊆ R d x_t \in V\subseteq \R^d xt∈V⊆Rd
- 付出损失 ℓ t : V → R \ell_t: V \rightarrow \R ℓt:V→R 来衡量算法在每一轮中的预测效果如何
- 集合 V V V 称为可行集(feasible set)
另外,让我们考虑一个任意的预测器 u in V ⊆ R d \pmb u~ \text{in}~V\subseteq \R^d u in V⊆Rd,将它的悔值参数化为 Regret T ( u ) \text{Regret}_T(\pmb u) RegretT(u),因此在线学习无非是设计和分析算法,以最小化对任意竞争者的损失函数序列的悔值。
Regret T ( u ) : = ∑ t = 1 T ℓ t ( x t ) − ∑ t = 1 T ℓ t ( u ) \text{Regret}_T(\pmb u):=\sum_{t=1}^T \ell_t(\pmb x_t) - \sum_{t=1}^T \ell_t(\pmb u)~ RegretT(u):=t=1∑Tℓt(xt)−t=1∑Tℓt(u)
在线学习可以分析如下问题:
- 点击预测问题
- 网络上的路由
- 重复博弈的均衡收敛
让我们重新回到猜数字问题,通过它,我们将揭示在线学习算法及其分析中的大部分关键成分。
2.2 取得胜利的策略
我们能赢得猜数字游戏吗?值得注意的是,我们没有假设对手如何决定数字。事实上,数字可以以任何方式生成,甚至可以根据我们的策略以自适应方式生成。这些数字可以一敌对的方式生成,目的就是让我们输掉比赛。这就是为什么我们称生成数字的机制为对手(adversary)。
让我们尝试设计一种策略,使得不管对手如何选择数字,悔值在时间上总是次线性的。首先看一下事后的最佳策略,即悔值的第二项最小值:
x T ⋆ : = argmin x ∈ [ 0 , 1 ] ∑ t = 1 T ( x − y t ) 2 = 1 T ∑ t = 1 T y t x^\star_T := \underset{x \in [0,1]}{\text{argmin}} \ \sum_{t=1}^T (x - y_t)^2 = \frac{1}{T} \sum_{t=1}^T y_t xT⋆:=x∈[0,1]argmin t=1∑T(x−yt)2=T1t=1∑Tyt
由于我们无法预知未来,可以肯定的是不能用 x T ⋆ x^\star_T xT⋆ 作为我们在每一轮的猜测值。但是我们知道过去,所以每一轮的合理策略可以是输出过去的最佳数字。为什么这样的策略会有效呢?并不是因为我们期望未来会像过去一样,而是我们想利用这样一个事实:最佳猜测在各轮之间不应变化太大。
因此,在轮次 t t t 我们的策略是去猜测 x t = x t − 1 ⋆ = 1 t − 1 ∑ i = 1 t − 1 y i x_t = x_{t-1}^\star=\frac{1}{t-1} \sum_{i=1}^{t-1} y_i xt=xt−1⋆=t−11∑i=1t−1yi. 这样的策略被称为 F o l l o w − t h e − L e a d e r Follow-the-Leader Follow−the−Leader (FTL), 因为我们在遵循过去几轮的最佳做法 (the Leader)。
现在让我们试着证明这个策略确实会让我们赢得这场比赛。
引理1.1 设 V ⊆ R d V \subseteq \R^d V⊆Rd 以及 ℓ t : V → R \ell_t :V \rightarrow \R ℓt:V→R 是一个任意的损失函数序列。用 x t ⋆ x^\star_t xt⋆ 表示 V V V 中前 t t t 轮的累计损失的最小值,那么,我们有:
∑ t = 1 T ℓ t ( x t ⋆ ) ≤ ∑ t = 1 T ℓ t ( x T ⋆ ) \sum_{t=1}^T \ell_t(x^\star_{t}) \leq \sum_{t=1}^T \ell_t(x^\star_{T}) t=1∑Tℓt(xt⋆)≤t=1∑Tℓt(xT⋆)
证明 我们通过对 T T T 的归纳来证明它。首先有
ℓ 1 ( x 1 ⋆ ) ≤ ℓ 1 ( x 1 ⋆ ) \ell_1(x^\star_1) \leq \ell_1(x^\star_{1}) ℓ1(x1⋆)≤ℓ1(x1⋆)
, 然后对于 T ≥ 2 T\geq2 T≥2,假设 ∑ t = 1 T − 1 ℓ t ( x t ⋆ ) ≤ ∑ t = 1 T − 1 ℓ t ( x T − 1 ⋆ ) \sum_{t=1}^{T-1} \ell_t(x^\star_{t}) \leq \sum_{t=1}^{T-1} \ell_t(x^\star_{T-1}) ∑t=1T−1ℓt(xt⋆)≤∑t=1T−1ℓt(xT−1⋆)为真,我们必须证明
∑ t = 1 T ℓ t ( x t ⋆ ) ≤ ∑ t = 1 T ℓ t ( x T ⋆ ) \sum_{t=1}^T \ell_t(x^\star_{t}) \leq \sum_{t=1}^T \ell_t(x^\star_{T}) t=1∑Tℓt(xt⋆)≤t=1∑Tℓt(xT⋆)
这个不等式等价于
∑ t = 1 T − 1 ℓ t ( x t ⋆ ) ≤ ∑ t = 1 T − 1 ℓ t ( x T ⋆ ) (1.3) \sum_{t=1}^{T-1} \ell_t(x^\star_{t}) \leq \sum_{t=1}^{T-1} \ell_t(x^\star_{T}) \tag{1.3} t=1∑T−1ℓt(xt⋆)≤t=1∑T−1ℓt(xT⋆)(1.3)
我们去掉了累加和的最后一个元素,因为它们是相同的。由于有:
∑ t = 1 T − 1 ℓ t ( x t ⋆ ) ≤ ∑ t = 1 T − 1 ℓ t ( x T − 1 ⋆ ) (1.3.1) \sum_{t=1}^{T-1} \ell_t(x^\star_{t}) \leq \sum_{t=1}^{T-1} \ell_t(x^\star_{T-1}) \tag{1.3.1} t=1∑T−1ℓt(xt⋆)≤t=1∑T−1ℓt(xT−1⋆)(1.3.1)
由于 x T − 1 ⋆ ≤ x T ⋆ x^\star_{T-1} \le x^\star_{T} xT−1⋆≤xT⋆,有
∑ t = 1 T − 1 ℓ t ( x T − 1 ⋆ ) ≤ ∑ t = 1 T − 1 ℓ t ( x T ⋆ ) (1.3.2) \sum_{t=1}^{T-1} \ell_t(x^\star_{T-1}) \leq \sum_{t=1}^{T-1} \ell_t(x^\star_{T}) \tag{1.3.2} t=1∑T−1ℓt(xT−1⋆)≤t=1∑T−1ℓt(xT⋆)(1.3.2)
由 ( 1.3.1 ) (1.3.1) (1.3.1)和 ( 1.3.2 ) (1.3.2) (1.3.2)可得 ( 1.3 ) (1.3) (1.3)为真。
上面的引理量化了这样一种观点,即知道未来并适应它通常比不适应它要好。有了这个引理,我们现在可以证明悔值将亚线性增长,而且它将在时间上是对数的(logarithmic)。
定理 1.2 设 y t ∈ [ 0 , 1 ] y_t \in [0,1] yt∈[0,1] 对于 t = 1 , … , T t=1,\dots,T t=1,…,T 是一个数字序列。使算法的输出为 x t = x t − 1 ⋆ : = 1 t − 1 ∑ i = 1 t − 1 y i x_t=x_{t-1}^\star:=\frac{1}{t-1}\sum_{i=1}^{t-1} y_i xt=xt−1⋆:=t−11∑i=1t−1yi。 于是有:
Regret T = ∑ t = 1 T ( x t − y t ) 2 − min x ∈ [ 0 , 1 ] ∑ t = 1 T ( x − y t ) 2 ≤ 4 + 4 ln T \text{Regret}_T = \sum_{t=1}^T (x_t - y_t)^2 - \min_{x \in [0,1]} \ \sum_{t=1}^T (x - y_t)^2 \leq 4 + 4\ln T RegretT=t=1∑T(xt−yt)2−x∈[0,1]min t=1∑T(x−yt)2≤4+4lnT
证明 我们使用引理1来确定悔值的上界:
∑ t = 1 T ( x t − y t ) 2 − min x ∈ [ 0 , 1 ] ∑ t = 1 T ( x − y t ) 2 = ∑ t = 1 T ( x t − 1 ⋆ − y t ) 2 − ∑ t = 1 T ( x T ⋆ − y t ) 2 ≤ ∑ t = 1 T ( x t − 1 ⋆ − y t ) 2 − ∑ t = 1 T ( x t ⋆ − y t ) 2 \sum_{t=1}^T (x_t - y_t)^2 - \min_{x \in [0,1]} \ \sum_{t=1}^T (x - y_t)^2 = \sum_{t=1}^T (x^\star_{t-1} - y_t)^2 - \sum_{t=1}^T (x^\star_T - y_t)^2 \leq \sum_{t=1}^T (x^\star_{t-1} - y_t)^2 - \sum_{t=1}^T (x^\star_t - y_t)^2 t=1∑T(xt−yt)2−x∈[0,1]min t=1∑T(x−yt)2=t=1∑T(xt−1⋆−yt)2−t=1∑T(xT⋆−yt)2≤t=1∑T(xt−1⋆−yt)2−t=1∑T(xt⋆−yt)2
现在,让我们来看看最后一个等式中总和的每一个差值,有:
( x t − 1 ⋆ − y t ) 2 − ( x t ⋆ − y t ) 2 = ( x t − 1 ⋆ ) 2 − 2 y t x t − 1 ⋆ − ( x t ⋆ ) 2 + 2 y t x t ⋆ = ( x t − 1 ⋆ + x t ⋆ − 2 y t ) ( x t − 1 ⋆ − x t ⋆ ) ≤ ∣ x t − 1 ⋆ + x t ⋆ − 2 y t ∣ ∣ x t − 1 ⋆ − x t ⋆ ∣ ≤ 2 ∣ x t − 1 ⋆ − x t ⋆ ∣ = 2 ∣ 1 t − 1 ∑ i = 1 t − 1 y i − 1 t ∑ i = 1 t y i ∣ = 2 ∣ ( 1 t − 1 − 1 t ) ∑ i = 1 t − 1 y i − y t t ∣ ≤ 2 ∣ 1 t ( t − 1 ) ∑ i = 1 t − 1 y i ∣ + 2 ∣ y t ∣ t ≤ 2 t + 2 ∣ y t ∣ t ≤ 4 t . \begin{aligned} (x^\star_{t-1} - y_t)^2 - (x^\star_t - y_t)^2 &= (x^\star_{t-1})^2 - 2 y_t x^\star_{t-1} - (x^\star_{t})^2 + 2 y_t x^\star_{t} \\ &= (x^\star_{t-1}+x^\star_{t} - 2y_t)(x^\star_{t-1}-x^\star_{t}) \\ &\leq |x^\star_{t-1}+x^\star_{t} - 2y_t|\,|x^\star_{t-1}-x^\star_{t}| \\ &\leq 2 |x^\star_{t-1}-x^\star_{t}| \\ &=2\left|\frac{1}{t-1} \sum_{i=1}^{t-1} y_i -\frac{1}{t} \sum_{i=1}^{t} y_i\right| \\ &=2\left|\left(\frac{1}{t-1}-\frac{1}{t}\right) \sum_{i=1}^{t-1} y_i - \frac{y_t}{t}\right| \\ &\leq 2\left|\frac{1}{t(t-1)}\sum_{i=1}^{t-1} y_i\right| + \frac{2|y_t|}{t} \\ &\leq \frac{2}{t} + \frac{2|y_t|}{t} \\ &\leq \frac{4}{t}~. \end{aligned} (xt−1⋆−yt)2−(xt⋆−yt)2=(xt−1⋆)2−2ytxt−1⋆−(xt⋆)2+2ytxt⋆=(xt−1⋆+xt⋆−2yt)(xt−1⋆−xt⋆)≤∣xt−1⋆+xt⋆−2yt∣∣xt−1⋆−xt⋆∣≤2∣xt−1⋆−xt⋆∣=2 t−11i=1∑t−1yi−t1i=1∑tyi =2 (t−11−t1)i=1∑t−1yi−tyt ≤2 t(t−1)1i=1∑t−1yi +t2∣yt∣≤t2+t2∣yt∣≤t4 .
因此可得:
∑ t = 1 T ( x t − y t ) 2 − min x ∈ [ 0 , 1 ] ∑ t = 1 T ( x − y t ) 2 ≤ 4 ∑ t = 1 T 1 t \sum_{t=1}^T (x_t - y_t)^2 - \min_{x \in [0,1]} \ \sum_{t=1}^T (x - y_t)^2 \leq 4\sum_{t=1}^T\frac{1}{t} t=1∑T(xt−yt)2−x∈[0,1]min t=1∑T(x−yt)2≤4t=1∑Tt1
要获得最后一个和的上界,请注意,我们正在尝试找到图1.1中绿色区域的上界。从图中可以看到,它的上界可以是 1 t − 1 \frac{1}{t-1} t−11从 2 2 2 到 T + 1 T+1 T+1 的积分。所以,我们有
∑ t = 1 T 1 t ≤ 1 + ∫ 2 T + 1 1 t − 1 d t = 1 + ln T \sum_{t=1}^T\frac{1}{t} \leq 1+\int_{2}^{T+1} \frac{1}{t-1} dt = 1+ \ln T t=1∑Tt1≤1+∫2T+1t−11dt=1+lnT
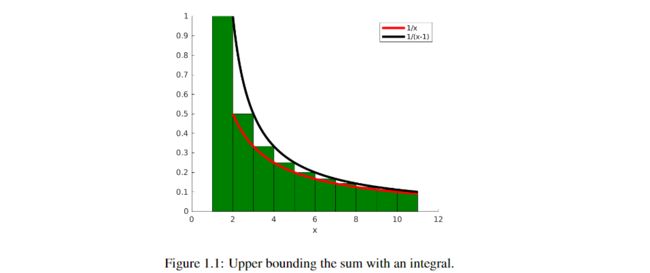
由于 ∣ x t ⋆ − x t − 1 ⋆ ∣ |x^\star_t-x^\star_{t-1}| ∣xt⋆−xt−1⋆∣非常快地趋于零,总悔值在时间上是次线性的。
关于这个策略,有几件事需要强调。该策略没有参数需要调整(如学习率、正则项)。请注意,参数的存在在在线学习中是没有意义的。我们只有一个数据流,不能在上面多次运行我们的算法来选择最好的参数。另外,它不需要保持过去的完整记录,而只需要通过运行平均数对其进行 “总结”。
