一篇科学的排队指南（简单线性回归和时间序列模型的应用）
大家日常生活中有时会需要抽签上场演讲、答辩、汇报或者即兴表演，如果是自娱自乐那还好，万一是诸如毕业论文答辩这样的重要场合，各种抽签玄学必然会广为流传。
想必大家都听过类似的说法：
“排名靠前才有优势，讲的内容不容易重复，评委们都会认真听，得分能高一些，排在后面评委都困了不会给高分的。”
“你可别乱说，苏格拉底最大的麦穗故事没听过吗，评委都喜欢把高分留在最后面。”
“哎呀你们都是扯淡，答辩都是多人评分，还去掉最高分和最低分，没有你们说的那么玄乎，前后都差不太多好吗。”
那么这些说法到底是不是真的有意义呢？今天我们用一次竞赛实际数据做一次小小的实验。
数据来源：某头部金融机构内部比赛评分。
数据说明：五个一组，即每评定五位选手之后评委休息讨论。
参考文献：
https://blog.csdn.net/yangwohenmai1/article/details/85071683
首先我们来看一下基本的数据情况：
sz=data['总分']
swz=data['未平滑总分']
plt.plot(sz)
plt.plot(swz, color="red")
plt.show()
print("variance:%f" % np.var(sz))
print("variance:%f" % np.var(swz))
虽然这个图（蓝色：去除最高分最低分之后选手平均分。红色：原始平均分）感觉不是特别明显，但是从方差来看，去除最高最低分之后数据波动性的确是下降了（11.771769→10.849152），那么这个对排序是否有影响呢？
再仔细观察一下，似乎先上场（1-10）号选手的得分波动率比后上场的选手波动率更大呢，而且这个一上一下的得分模式是什么意思，难不成存在均值回归（mean-reversion）特性吗？等一下，貌似有点跑题，本次小实验我们明明是想研究一下排序到底对选手得分有无实质性影响，好吧，那我们继续。
首先假设忽略异方差带来的影响，“强行”做线性回归，看看是什么样子呢？
timemodel = linear_model.LinearRegression()
timemodel.fit(timex, score)
coef = timemodel.coef_
intercept = timemodel.intercept_
R2 = timemodel.score(timex, score)
print('model expression: y = %f + %f*x' % (intercept, coef))
print('R-square: %f' % R2)
y_model=(time*coef) + intercept
plt.scatter(time, score)
plt.plot(time, y_model, color = "red")
plt.xlim([0,50])
plt.ylim([70,100])
plt.show()
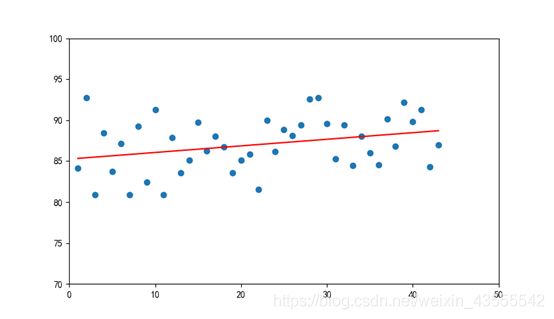数据散点图和拟合直线如图所示，
model expression: y = 85.246796 + 0.080597*x
R-square: 0.092207
可以看出，我们对“晚出场得分更优秀”的印象可以被正的斜率项所支持，从图形也可看出拟合模型存在升序。但是考虑到R2只有0.09实在是没有说服力，这个印象也只能是勉强被证实。从某种方面来讲，简单的一元回归似乎不适合用于解释排队的优劣。
那么我们换一种思路，假设排序真的对得分有影响，而这里的出场顺序因为是随机抽签，所以问题转化为一个时间序列问题，即出场时间是否对得分有影响。所以我们首先使用最简单的自回归模型（Autoregressive Model）做一个小测试。
先看一眼滞后一期的效果：
lag_plot(score)
plt.xlim([50,100])
plt.ylim([50,100])
plt.show()
看起来比较集中，但是本身数据量（43）较少，参考性不强。
那么我们直接看看更多滞后变量之间的关系：
autocorrelation_plot(score)
plt.show()
自相关摆动看起来存在一定的相关性了，介于20期滞后滞后性基本趋近于零，我们选择20期滞后作图让我们看的更仔细一点：
plot_acf(score, lags = 20)
plt.show()
结果与我们最先判断的“一上一下”有所不同，没想到滞后两期的影响力最大。好的那我们直接上终极武器，自回归模型来测试一下。首先我们假定最后五个得分未“看不见的”待预测真值。
score = data['总分'] #定义数据列
train, test = score[1:len(score)-5], score[len(score)-5:]
model = AR(train)
model_fit = model.fit()
print('Lag: %s' % model_fit.k_ar)
print('Coefficients: %s' % model_fit.params)
predictions = model_fit.predict(start=len(train), end=len(train)+len(test)-1, dynamic=False)
error = mean_squared_error(test, predictions)
print('Test MSE: %.3f' % error)
plt.plot(test)
plt.plot(predictions, color='red')
plt.show()
结果如下：
Lag: 9
Coefficients: const 44.125154
L1.总分 0.033900
L2.总分 0.628062
L3.总分 -0.073962
L4.总分 -0.306875
L5.总分 0.262276
L6.总分 0.038107
L7.总分 -0.399975
L8.总分 0.087084
L9.总分 0.225274
dtype: float64
Test MSE: 9.722
来看看预测图：
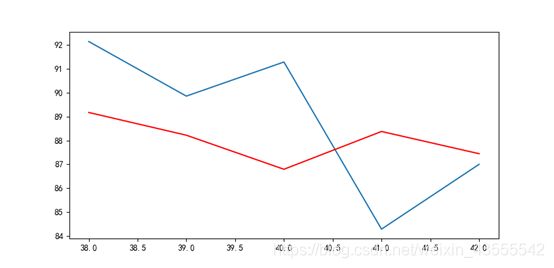红色为模型预测值，蓝色为真值。
除了第三和第四个值以外，其他预测值与真值相差均在一个标准差左右或更小，显示模型具备一定的参考意义。
那么如果是未平滑的总分呢？来看看结果：
Lag: 9
Coefficients: const 49.727994
L1.未平滑总分 0.013009
L2.未平滑总分 0.561009
L3.未平滑总分 -0.033115
L4.未平滑总分 -0.272347
L5.未平滑总分 0.213781
L6.未平滑总分 0.057796
L7.未平滑总分 -0.278225
L8.未平滑总分 0.051678
L9.未平滑总分 0.113565
dtype: float64
Test MSE: 12.409
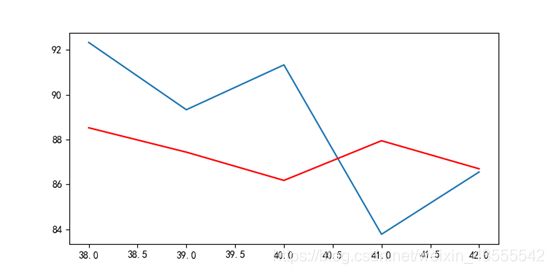比较而言，未平滑总分预测的MSE大于平滑总分（12.409> 9.722），还是平滑后得分的模型参考下更高一些。
综上所述你的前两位选手的表现，可能对你的表现影响更大，而平滑得分的确能够加强这种影响力。说人话就是，评委会刻意回避你前一位选手得分对你表现的影响，而下意识的选择前两位选手的表现作为你的打分“基础”。而排在后面的选手，的确会在得分上有一定的优势，因为评委在后期的打分会趋向于一致，波动性降低，且平均分会略高。某种意义上来说，评委在评分过程中也在被选手所训练，这的确很有意思。