卷积核的grad为none_pytorch入门与实践（1）：张量的基本操作和自动微分requires_grad=True...

PyTorch是一个基于Python的库，提供了一个具有灵活易用的深度学习框架，是近年来最受欢迎的深度学习框架之一。

如果你是新新新手，可以先学习以下教程： 深度学习之PyTorch实战-基础学习及搭建环境 PyTorch中文文档

改编自：

(1) DEEP LEARNING WITH PYTORCH: A 60 MINUTE BLITZ

(2) https://www.kesci.com/home/project/5e0038642823a10036ae9ebf/code

1 初识PyTorch

1.1 张量

1.导入pytorch包

import torch

2.创建一个未初始化的5x3张量

x = torch.empty(5, 3)
print(x)
tensor([[2.7517e+12, 7.5338e+28, 3.0313e+32],
        [6.3828e+28, 1.4603e-19, 1.0899e+27],
        [6.8943e+34, 1.1835e+22, 7.0976e+22],
        [1.8515e+28, 4.1988e+07, 3.0357e+32],
        [2.7224e+20, 7.7782e+31, 4.7429e+30]])

3.创建一个随机初始化的5x3张量

x = torch.rand(5, 3)
print(x)
tensor([[0.2218, 0.1979, 0.9491],
        [0.2082, 0.6139, 0.1096],
        [0.1491, 0.5660, 0.7435],
        [0.8009, 0.0788, 0.0223],
        [0.4252, 0.2422, 0.8202]])

4.创建一个5x3的0张量，类型为long

x = torch.zeros(5, 3, dtype=torch.long)
print(x)
tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])

5.直接从数组创建张量

x = torch.tensor([5.5, 3])
print(x)
tensor([5.5000, 3.0000])

6.创建一个5x3的单位张量，类型为double

x = torch.ones(5, 3, dtype=torch.double)
print(x)
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)

7.从已有的张量创建相同维度的新张量，并且重新定义类型为float

x = torch.randn_like(x, dtype=torch.float)
print(x)
tensor([[ 0.0385,  0.2725,  0.7144],
        [ 0.1436,  0.0642,  0.4125],
        [ 0.2571,  2.0826, -1.0106],
        [-0.4239,  0.6424,  1.3656],
        [-0.4444,  0.5675,  1.3937]])

8.打印一个张量的维度

print(x.size())
torch.Size([5, 3])

9.将两个张量相加

y = torch.rand(5, 3)
print(x + y)

# 方法二
# print(torch.add(x, y))

# 方法三
#result = torch.empty(5, 3)
#torch.add(x, y, out=result)
#print(result)

# 方法四
#y.add_(x)
#print(y)
tensor([[ 0.5639,  0.3429,  1.2488],
        [ 0.1815,  0.8415,  1.1878],
        [ 0.9620,  2.9639, -0.8427],
        [ 0.2482,  0.8666,  1.7800],
        [-0.1678,  1.1261,  1.5676]])

10.打印张量的第一列

print(x[:, 0]) #第一行
print(x[0]) #第一列
tensor([ 0.0385,  0.1436,  0.2571, -0.4239, -0.4444])
tensor([0.0385, 0.2725, 0.7144])

11.将一个4x4的张量resize成一个一维张量

x = torch.randn(4, 4)
y = x.view(16)
print(x.size(),y.size())
torch.Size([4, 4]) torch.Size([16])

12.将一个4x4的张量，resize成一个2x8的张量

y = x.view(2, 8)
print(x.size(),y.size())

# 方法二
z = x.view(-1, 8) # 确定一个维度，-1的维度会被自动计算
print(x.size(),z.size())
torch.Size([4, 4]) torch.Size([2, 8])
torch.Size([4, 4]) torch.Size([2, 8])

13.从张量中取出数字

x = torch.randn(1)
print(x)
print(x.item())
tensor([-1.2852])
-1.2852163314819336
x = torch.randn(2,2)
print(x)
print(x[1,1].item())
tensor([[-0.3501,  1.0590],
        [-1.0007, -0.4674]])
-0.46742647886276245

1.2 Numpy的操作

14.将张量装换成numpy数组

a = torch.ones(5)
print(a)

b = a.numpy()
print(b)
tensor([1., 1., 1., 1., 1.])
[1. 1. 1. 1. 1.]

15.将张量+1，并观察上题中numpy数组的变化

a.add_(1)
print(a)
print(b)
tensor([2., 2., 2., 2., 2.])
[2. 2. 2. 2. 2.]

16.从numpy数组创建张量

import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
print(a)
print(b)
[1. 1. 1. 1. 1.]
tensor([1., 1., 1., 1., 1.], dtype=torch.float64)

17.将numpy数组+1并观察上题中张量的变化

np.add(a, 1, out=a)
print(a)
print(b)
[2. 2. 2. 2. 2.]
tensor([2., 2., 2., 2., 2.], dtype=torch.float64)

2 自动微分

2.1 张量的自动微分

18.新建一个张量，并设置requires_grad=True

x = torch.ones(2, 2, requires_grad=True)
print(x)
tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

19.对张量进行任意操作（y = x + 2）

y = x + 2
print(y)
print(y.grad_fn) # y就多了一个AddBackward的对象
tensor([[3., 3.],
        [3., 3.]], grad_fn=)

20.再对y进行任意操作

z = y * y * 3
out = z.mean()

print(z) # z多了MulBackward的对象
print(out) # out多了MeanBackward的对象
tensor([[27., 27.],
        [27., 27.]], grad_fn=)
tensor(27., grad_fn=)

2.2 梯度

21.对out进行反向传播

out.backward()

22.打印梯度d(out)/dx

print(x.grad) #out=0.25*Σ3(x+2)^2
# d(out)/dx = 1/4 * 6x = 1.5x
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

23.创建一个结果为矢量的计算过程（y=x*2^n）

x = torch.randn(3, requires_grad=True)
print(x)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)
tensor([-0.1457,  0.0342,  0.1276], requires_grad=True)
tensor([-1193.1697,   279.8315,  1045.1823], grad_fn=)

24.计算v = [0.1, 1.0, 0.0001]处的梯度

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)
tensor([8.1920e+02, 8.1920e+03, 8.1920e-01])

25.关闭梯度的功能

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

# 方法二
# print(x.requires_grad)
# y = x.detach()
# print(y.requires_grad)
# print(x.eq(y).all())
True
True
False

3 神经网络

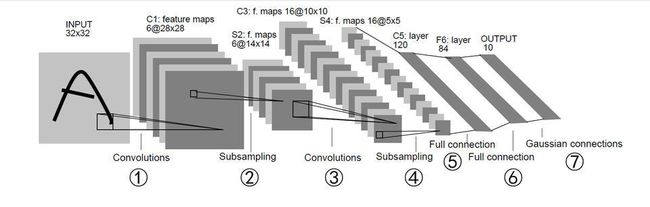
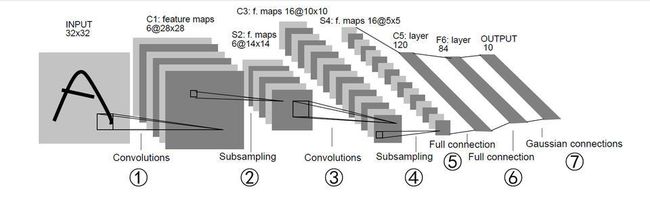
这部分会实现LeNet5，结构如下所示

3.1 定义网络

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 26.定义①的卷积层，输入为32x32的图像，卷积核大小5x5卷积核种类6
        self.conv1 = nn.Conv2d(3, 6, 5)
        # 27.定义③的卷积层，输入为前一层6个特征，卷积核大小5x5，卷积核种类16
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 28.定义⑤的全链接层，输入为16*5*5，输出为120
        self.fc1 = nn.Linear(16 * 5 * 5, 120)  # 6*6 from image dimension
        # 29.定义⑥的全连接层，输入为120，输出为84
        self.fc2 = nn.Linear(120, 84)
        # 30.定义⑥的全连接层，输入为84，输出为10
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # 31.完成input-S2，先卷积+relu，再2x2下采样
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # 32.完成S2-S4，先卷积+relu，再2x2下采样
        x = F.max_pool2d(F.relu(self.conv2(x)), 2) #卷积核方形时，可以只写一个维度
        # 33.将特征向量扁平成行向量
        x = x.view(-1, 16 * 5 * 5)
        # 34.使用fc1+relu
        x = F.relu(self.fc1(x))
        # 35.使用fc2+relu
        x = F.relu(self.fc2(x))
        # 36.使用fc3
        x = self.fc3(x)
        return x


net = Net()
print(net)
Net(
  (conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

37.打印网络的参数

params = list(net.parameters())
# print(params)
print(len(params))
10

38.打印某一层参数的形状

print(params[0].size())
torch.Size([6, 3, 5, 5])

39.随机输入一个向量，查看前向传播输出

input = torch.randn(1, 3, 32, 32)
print(input.size()) # 1个样本，3个channel，32*32像素
print(input)
out = net(input)
print(out)
torch.Size([1, 3, 32, 32])
tensor([[[[ 0.8842,  0.3144, -0.3450,  ...,  1.3449,  0.5608,  0.3913],
          [ 1.2463, -0.6526, -0.8858,  ...,  1.8576,  0.1731, -1.8414],
          [ 0.6541, -1.7835,  1.1173,  ...,  0.9162,  0.0133, -1.2699],
          ...,
          [ 0.2942, -1.3088,  1.2589,  ..., -0.3612, -0.2821,  0.3796],
          [-1.2562,  0.4472, -0.0288,  ...,  0.7728,  0.4552, -1.1600],
          [-1.3940, -0.1773,  0.2355,  ...,  0.0686,  0.1527,  0.7244]],

         [[-0.9507,  1.3473,  0.1791,  ..., -0.8668, -0.1624, -1.0063],
          [ 2.0376,  0.0706, -0.4181,  ..., -0.7650, -0.9501,  0.8084],
          [-0.2065, -0.5103, -1.1074,  ...,  0.8636, -0.8002, -0.5690],
          ...,
          [-0.4108,  0.5790, -1.2921,  ...,  0.4494,  0.3363,  0.6388],
          [-0.7036, -1.3791, -1.6519,  ...,  0.7853, -0.1587, -0.6029],
          [-0.7042, -0.2481, -0.5580,  ..., -0.9274, -0.8770,  0.5443]],

         [[-1.0507, -1.0034, -0.9321,  ...,  0.7069,  0.8155, -1.2291],
          [-0.4410, -0.9667,  0.3475,  ..., -0.7563,  2.0873, -0.9078],
          [-0.2733, -0.2245,  1.7173,  ..., -0.4200, -1.6980,  0.7572],
          ...,
          [ 0.9761,  0.7852,  0.1797,  ...,  0.5471,  1.1544, -1.7472],
          [-0.2204, -0.9797, -0.3549,  ..., -0.8765,  0.2938,  0.5266],
          [-1.7714,  0.1623, -0.7405,  ..., -1.4199,  0.1131,  0.4714]]]])
tensor([[ 0.0688,  0.0990,  0.0778,  0.0592,  0.0277, -0.0268, -0.0284, -0.0938,
         -0.1056,  0.0487]], grad_fn=)

40.将梯度清零

net.zero_grad()

41.随机一个梯度进行反向传播

print(torch.randn(1, 10))
out.backward(torch.randn(1, 10))
tensor([[-0.8285,  0.2922,  0.5672, -0.1644, -2.0075,  0.0337,  2.2223, -0.3571,
          1.1908,  0.8642]])

3.2 损失函数

42.用自带的MSELoss()定义损失函数

criterion = nn.MSELoss()

43.随机一个真值，并用随机的输入计算损失

target = torch.randn(10)  # 随机真值
print(target)
target = target.view(1, -1)  # 变成行向量
print(target)

output = net(input)  # 用随机输入计算输出
print(output)

loss = criterion(output, target)  # 计算损失
print(loss)
tensor([-0.4188,  0.1543,  0.8085, -1.9596,  0.5578, -0.2232,  0.4089,  2.4674,
        -0.1676, -0.9115])
tensor([[-0.4188,  0.1543,  0.8085, -1.9596,  0.5578, -0.2232,  0.4089,  2.4674,
         -0.1676, -0.9115]])
tensor([[ 0.0688,  0.0990,  0.0778,  0.0592,  0.0277, -0.0268, -0.0284, -0.0938,
         -0.1056,  0.0487]], grad_fn=)
tensor(1.2847, grad_fn=)

44.将梯度初始化，计算上一步中loss的反向传播

net.zero_grad()

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])

45.计算43中loss的反向传播

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
conv1.bias.grad after backward
tensor([ 0.0101,  0.0003, -0.0068, -0.0084,  0.0030,  0.0060])

3.3 更新权重

46.定义SGD优化器算法，学习率设置为0.01

import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.01)

46.使用优化器更新网络的权重

optimizer.zero_grad()
output = net(input)
loss = criterion(output, target)
loss.backward()

# 更新权重
optimizer.step()