【深度学习】《深度学习理论与实战(基础篇)》第一章学习笔记

本文章为《深度学习理论与实战（基础篇）》学习笔记。

机器学习

机器学习是深度学习一个重要的子领域，研究让如何让机器自动学习出模型或者规则，来解决实际问题，研究者大多使用统计方法来构建一套模型或者规则来解决问题，通过泛化能力来判断模型的通用性，提出了支持向量机模型。
基于统计的模型的机器学习中的主流，包括逻辑回归(Logistic Regression)、朴素贝叶斯（Naive Bayes）分类器、隐马尔可夫模型（Hidden Markov Model）等。

0 机器学习的基本概念

我们给机器建立一个模型，从数学的角度来说一个模型就是一个函数，它的输入一般是一个向量（例如二维矩阵，如图片，或者三维张量，如视频），模型的输出（现实问题的解答）可能是离散的标签，我们称这类问题为分类问题；模型的输出使连续的，我们成为回归问题。
从本质上讲，智能就是学习过去，感知现在，预测未来。

损失函数（Loss Function）：用来判断模型的输出的正确性，损失越大说明模型错的越离谱，损失越小说明模型错的不算多，我们追求损失小的模型，从另一方面来说损失越小可以说明模型的准确率更高。

泛化能力其实说的模型的通用性，如果模型对训练集学习的过于精细，学习到的不是本质的特征或规则，则会导致在在训练集上训练结果优异，但在测试集上结果很差，我们通常在验证阶段（Validation）对模型的泛化能力进行评估。

机器学习可分为：监督学习、无监督学习、强化学习

1监督学习

训练数据集通常为 数据+标签 的形式。

监督学习可分为回归问题和分类问题
回归问题：比如预测温度，输出是一个连续的实数
分类问题：恶意流量识别二分类问题，输出的是离散的标签

1.1 常见的监督学习模型

1.1.1 朴素贝叶斯分类器

强假设：处理的样本特征在给定的分类条件下都是相互独立的。

1.1.2 逻辑回归

逻辑回归是一个线性模型，线性模型是最简单的模型。最简单的线性回归模型是$y=w^T+b$。

线性模型的输出范围是$-\infty$到$+\infty$，通常我们使用Sigmoid函数，将线性模型的输出范围从$-\infty$到$+\infty$映射到(0,1)，后可根据输出的数字判断分类结果。
$$\sigma (x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1},.$$

把线性变换的结果应用一次到Sigmoid函数，这样输出结果就是0~1之间，此时逻辑回归模型可以看做
$$f(x)=\frac{1}{1+e^{-(w^{T}x+b)}}$$
之后训练时使用损失函数和梯度下降优化算法，学习到最优的参数$w$和$b$。
逻辑回归可以推广为多分类逻辑回归（Mulinomial Logisitic Regression），也叫作最大熵模型（Maximum Entropy），是自然语言处理（NLP）中广为人知。

1.1.3 支持向量机

支持向量机（Support Vector Machine，SVM）的基本思想是用一条直线（推广到多维空间时是超平面）来划分两类数据，通过判断划分的直线与两类数据之间的距离，来评估模型的优劣，距离越大越好。对于线性不可分的情况，引入松弛因子来乘法分类错误的数据。

SVM可以使用核函数（Kernel Function）来处理非线性场景，即先将非线性场景的数据集映射到高维空间中，在高维空间中使用支持向量机找到一个超平面。

1.1.4 决策树

决策树（Decision Tree）构建时遇到的最本质的问题，首先按照哪个属性进行划分合适？可以使用基尼系数（Gini）或者信息熵进行评估，选取信息增益最大的那一个。
随机森林则是构造多棵决策树，每个决策树随机挑选特征进行构造，最后分类预测时进行投票决定分类。

2 无监督学习

训练数据只有输入而没有分类标签等输出，目标是根据数据的分布发现数据的规律。常见的任务包括降维和聚类，目前比较热门的生成对抗网络GAN就属于无监督学习。

降维的目的是把高维空间的点减到一个低维空间上，同时尽可能地保留原始数据之间的关系、信息，方便之后使用模型进行训练及预测，降维有效的应对了维灾难，提高了模型的效率。

3 强化学习

监督学习本质上是一种知识的传递，但不能发现新的知识。
强化学习的主体是可以通过行为影响环境的，我们每走的一步都有可能变好或者变坏。

强化学习解决的核心问题是给定一个状态，判断它的价值（Value）。价值和奖励（Reward）是强化学习最基本的两个概念。对于强化学习的主体（Agent）来说，奖励是立刻获得的，价值则是之后不久或者很久之后才可以计算的。
强化学习的本质就是主体通过与环境（Environment）互动来学习怎么达成一个目标。主题会持续地与环境交互，根据当前的状态选择行为（Action），而环境会给主体新的状态和奖励。

4 衡量指标

衡量指标使用来评估模型好坏的指标。

预测为正例的正例：TP
预测为正例的负例：FP
预测为负例的负例：TN
预测为负例的正例：FN

准确率（Accuracy），即预测正确的记录占全部记录的比例：$$\frac{TP+TN}{TP+FP+TN+FN}$$
精确率（Precision）是针对每个分类的，即本类正确预测的记录数占预测为本类记录数的比例：$$\frac{TP}{TP+FP}$$
召回率（Recall）是针对每个分类的，即正确预测为本类的记录数占全部预测为本类的记录数的比例：$$\frac{TP}{TP+FN}$$
F1值：
$$F_{1Score}=\frac{2}{\frac{1}{precision}+\frac{1}{recall}}$$
macro F1：所有类的F1值相加在取平均。
micro F1：所有类的F1值加权相加。
※精确率和召回率是相互矛盾的两个指标，而$F_1$是一个平衡的指标，既考虑精确率又考虑召回率。

5 损失函数

有了衡量的指标，还需要定一个损失函数（也叫目标函数）来衡量参数的好坏。

损失函数中涉及到torch编程中要设置的参数（或选用的算法）有：

1. 梯度下降算法

我们通常定义一个连续可导的损失函数来代替准确率这样的指标，我们对损失函数的期望是——损失函数越小，准确率越高才行。
最常见的损失函数如交叉熵（Cross Entropy）：
$$H(p,q)=-\sum _{x}p(x)lo{g}_{2}q(x)$$上述公式中，p是真实分布，q是预测的分布。
对于多分类器的输出之和不一定为1，我们可以使用$Softmax$函数把多分类的向量进行归一化，使处理后的向量每一项之和等于1，之后根据极大似然估计，找出预测类。
$$Softmax(x_1,x_2,...,x_n{)}^T=(\frac{e^{x_1}}{e^{x_1}+...+e^{x_n}}+...+\frac{e^{x_1}}{e^{x_n}+...+e^{x_n}})$$

6 优化与梯度下降

梯度下降的过程中涉及到torch编程中要设置的参数（或选用的算法）有：

1. 学习率
2. batchsize
3. 梯度下降算法

我们所求的梯度，是所有训练数据的损失的梯度。

需要进行梯度下降的原因：

1. 有了准确率我们可以评估模型的好坏，有了损失函数我们可以评估参数的好坏，此时我们需要一种算法来不断地帮我们调整参数，以此来找到“最优”参数。
2. 梯度下降即，沿着梯度的反方向走一点，保证损失函数是变小的，我们在调整参数的过程中每次要调整多大的比例，用$\eta$表示，这就称为学习率（Learning Rate）。（自我理解是沿着当前函数发展方向进行回调）
3. 我们将参数进行了微调之后，就要重新判断参数的好坏，这是就要使用损失函数进行评估，进行评估时如果使用全部的数据进行评估，会出现执行速度非常慢的问题，同时可能出现内存不够用的问题，为了应对此时出现的问题，可以从数据集中进行随机抽样，用抽样出来的数据来对参数进行评估，抽样的数据量的大小就成为批处理大小(batch size)。

随机梯度算法（Stochastic Gradient Descent，SGD）即引入随机的因素，不必每次对所有训练数据的损失求梯度，而是随机的选取一个batchsize的训练数据来计算梯度。
随机梯度算法是在神经网络中最常用的算法。

梯度下降讲解视频：
如何通俗地解释梯度下降法
[5分钟深度学习] #01 梯度下降算法

7 过拟合与欠拟合

7.1 数据集的划分

划分为训练集、测试集。
常用的方法：k折交叉验证

7.2 正则化

正则化是处理过拟合的一种方法，它的损失函数需要在加上一个正则项，并设置一个正则项的影响因子$\lambda$，超参数$\lambda$用来控制拟合的损失和正则项。$\lambda$的选择要慎重，过大可能导致欠拟合，过小则不能解决过拟合的问题。

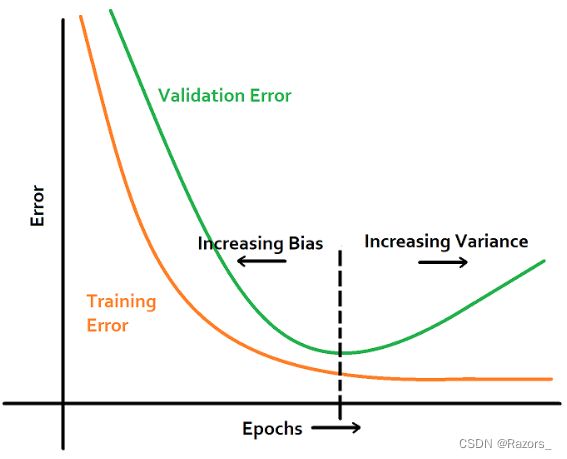
7.3 Early-stop

涉及到的编程中的参数为：

1. 迭代次数（Epochs）

对于不同的迭代次数，我们的模型通常有如下图的结果

我们可以对同一个模型的训练设置不同的训练迭代次数，每次迭代结束后对模型进行评估，如果从评估指标上该模型是较好的，则保存该模型。

其他预防过拟合的方法包括数据增强、Dropout以及各种正则化等方法。