UVa 10256 (判断两个凸包相离) The Great Divide

题意：

给出n个红点，m个蓝点。问是否存在一条直线使得红点和蓝点分别分布在直线的两侧，这些点不能再直线上。

分析：

求出两种点的凸包，如果两个凸包相离的话，则存在这样一条直线。

判断凸包相离需要判断这两件事情：

1. 任何一个凸包的任何一个顶点不能在另一个凸包的内部或者边界上。
2. 两个凸包的任意两边不能相交。

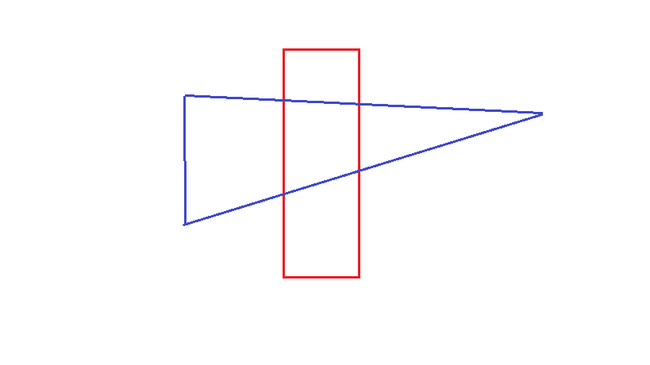
二者缺一不可，第一条很好理解，但为什么还要判断第二条，因为存在这种情况：

虽然每个凸包的顶点都在另一个凸包的外部，但两个凸包明显是相交的。

 

  1 //#define LOCAL
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <cmath>
  6 #include <vector>
  7 using namespace std;
  8 
  9 const int maxn = 500 + 10;
 10 const double eps = 1e-10;
 11 const double PI = acos(-1.0);
 12 
 13 int dcmp(double x)
 14 {
 15     if(fabs(x) < eps)    return 0;
 16     else return x < 0 ? -1 : 1;
 17 }
 18 
 19 struct Point
 20 {
 21     double x, y;
 22     Point(double x=0, double y=0):x(x), y(y) {}
 23 };
 24 typedef Point Vector;
 25 Point operator + (Point a, Point b) { return Point(a.x+b.x, a.y+b.y); }
 26 Point operator - (Point a, Point b) { return Point(a.x-b.x, a.y-b.y); }
 27 Point operator * (Point a, double p) { return Point(a.x*p, a.y*p); }
 28 Point operator / (Point a, double p) { return Point(a.x/p, a.y/p); }
 29 bool operator < (Point a, Point b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }
 30 bool operator == (Point a, Point b) { return a.x == b.x && a.y == b.y; }
 31 
 32 double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
 33 double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
 34 
 35 bool SegmentIntersection(Point a1, Point a2, Point b1, Point b2)
 36 {
 37     double c1 = Cross(a2-a1, b1-a1), c2 = Cross(a2-a1, b2-a1);
 38     double c3 = Cross(b2-b1, a1-b1), c4 = Cross(b2-b1, a2-b1);
 39     return dcmp(c1*c2) < 0 && dcmp(c3*c4) < 0;
 40 }
 41 
 42 bool OnSegment(Point p, Point a, Point b)
 43 {//点是否在线段上，不包含在端点处的情况 
 44     return dcmp(Cross(a-p, b-p)) == 0 && dcmp(Dot(a-p, b-p)) < 0;
 45 }
 46 
 47 vector<Point> ConvexHull(vector<Point> p)
 48 {
 49     sort(p.begin(), p.end());
 50     p.erase(unique(p.begin(), p.end()), p.end());
 51     
 52     int n = p.size();
 53     int m = 0;
 54     vector<Point> ch(n+1);
 55     for(int i = 0; i < n; ++i)
 56     {
 57         while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
 58         ch[m++] = p[i];
 59     }
 60     int k = m;
 61     for(int i = n-2; i >= 0; --i)
 62     {
 63         while(m > k && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
 64         ch[m++] = p[i];
 65     }
 66     if(m > 1) m--;
 67     ch.resize(m);
 68     return ch;
 69 }
 70 
 71 int IsPointInPolygon(Point p, const vector<Point>& poly)
 72 {
 73     int wn = 0;
 74     int n = poly.size();
 75     for(int i = 0; i < n; ++i)
 76     {
 77         if(OnSegment(p, poly[i], poly[(i+1)%n])) return -1;    //边界 
 78         int k = dcmp(Cross(poly[(i+1)%n]-poly[i], p-poly[i]));
 79         int d1 = dcmp(poly[i].y-p.y);
 80         int d2 = dcmp(poly[(i+1)%n].y-p.y);
 81         if(k > 0 && d1 <= 0 && d2 > 0) wn++;
 82         if(k < 0 && d2 <= 0 && d1 > 0) wn--;
 83     }
 84     if(wn)    return 1;    //内部 
 85     return 0;            //外部 
 86 }
 87 
 88 bool ConvexPolygonDisjiont(const vector<Point> ch1, const vector<Point> ch2)
 89 {
 90     int c1 = ch1.size(), c2 = ch2.size();
 91     for(int i = 0; i < c1; ++i)
 92         if(IsPointInPolygon(ch1[i], ch2) != 0) return false;
 93     for(int i = 0; i < c2; ++i)
 94         if(IsPointInPolygon(ch2[i], ch1) != 0) return false;
 95     for(int i = 0; i < c1; ++i)
 96           for(int j = 0; j < c2; ++j)
 97             if(SegmentIntersection(ch1[i], ch1[(i+1)%c1], ch2[j], ch2[(j+1)%c2])) return false;
 98     return true;
 99 }
100 
101 int main(void)
102 {
103     #ifdef LOCAL
104         freopen("10256in.txt", "r", stdin);
105     #endif
106     
107     int n, m;
108     while(scanf("%d%d", &n, &m) == 2)
109     {
110         if(!n && !m) break;
111         vector<Point> p1, p2;
112         double x, y;
113         for(int i = 0; i < n; ++i)
114         {
115             scanf("%lf%lf", &x, &y);
116             p1.push_back(Point(x, y));
117         }
118         for(int i = 0; i < m; ++i)
119         {
120             scanf("%lf%lf", &x, &y);
121             p2.push_back(Point(x, y));
122         }
123         if(ConvexPolygonDisjiont(ConvexHull(p1), ConvexHull(p2)))    puts("Yes");
124         else puts("No");
125     }
126     
127     return 0;
128 }

代码君