为什么理想滤波器不可实现
系统对于信号的作用大体可分为两类:一类是信号的传输,一类是滤波。信号传输要求信号尽量不失真,而滤波则要求滤去或削弱不需要的成分,必然伴随着失真。接下来,本文将从信号的无失真传输来引入信号的滤波,进而详细阐明为什么理想滤波器不可实现。
1. 无失真传输
想必大家都了解过接力传话游戏,往往传到最后会与最初的表达千差万别,也就是产生了失真,这在信号传输过程中是要极力避免的。
1.1 定义
信号无失真传输是指系统的输出信号与输入信号相比,只有幅度的大小和出现时间的先后不同,而没有波形上的变化。
也就是说输出信号的形状应是输入信号经过拉伸或压缩变换加上平移变换的组合,这样的好处是在信号输出端,可以轻而易举的还原出原信号。举个具体的例子吧,若输入信号为 f ( t ) f(t) f(t) , 经过传输系统后的输出为 y ( t ) y(t) y(t) , 如果系统是无失真传输系统的话, f ( t ) 、 y ( t ) f(t)、y(t) f(t)、y(t) 应该满足的关系大概是下面这样的:
若用严格的数学表达式来形容经过无失真传输系统后输入信号 f ( t ) f(t) f(t) 和输出信号 y ( t ) y(t) y(t) 的关系,则为:
y ( t ) = K f ( t − t d ) y(t)=K f\left(t-t_{d}\right) y(t)=Kf(t−td)
对等号两边分别进行傅里叶变换,根据 傅里叶变换的时移特性 ,得到输入输出的频谱关系:
Y ( j ω ) = K e − j ω t d F ( j ω ) Y(j \omega)=K e^{-j \omega t_{d}} F(j \omega) Y(jω)=Ke−jωtdF(jω)
1.2 无失真传输条件
对系统的冲激响应 h ( t ) h(t) h(t) 的要求:
h ( t ) = K δ ( t − t d ) h(t)=K \delta\left(t-t_d\right) h(t)=Kδ(t−td)
对系统传输函数(频率响应函数) H ( j ω ) H(j\omega) H(jω) 的要求:
H ( j ω ) = Y ( j ω ) / F ( j ω ) = K e − j ω t d 即 ∣ H ( j ω ) ∣ = K , θ ( ω ) = − ω t d \begin{array}{c} H(j \omega)=Y(j \omega) / F(j \omega)=K e^{-j \omega t_{d}}\\ \text {即} \quad |{H}({j} \omega)|={K}, \quad \theta(\omega)=-\omega{t}_{{d}}\\ \end{array} H(jω)=Y(jω)/F(jω)=Ke−jωtd即∣H(jω)∣=K,θ(ω)=−ωtd
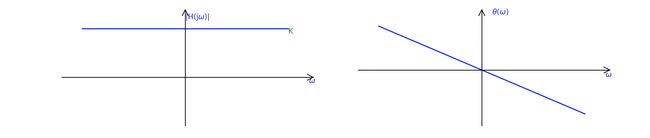
所以在无失真传输条件下,系统的幅频特性 ∣ H ( j ω ) ∣ |H(j\omega)| ∣H(jω)∣ 和相频特性 θ ( ω ) \theta(\omega) θ(ω) 应如下图所示:
要说明的是,上述条件是信号无失真传输的理想条件。当传输有限带宽的信号时,只要在信号占有频带范围内,系统的幅频、相频特性满足以上条件即可。比如我们要传输人类说话的语音信号,那么只要保证在20000Hz以内,传输系统的幅频特性 ∣ H ( j ω ) ∣ |H(j\omega)| ∣H(jω)∣ 和相频特性 θ ( ω ) \theta(\omega) θ(ω) 要满足如上要求即可。
2. 理想低通滤波器
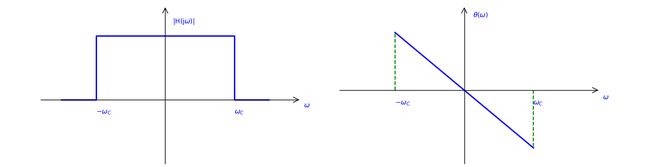
如果把滤波器看成一个系统,顾名思义,理想低通滤波器的作用应该是:高于设定的某个频率 f C f_C fC 的波形成分将从原信号中滤除。这个设定的频率 f C f_C fC 被称为截止频率,其对应的截止角频率记为 ω C = 2 π f C \omega_C=2\pi f_C ωC=2πfC ,该系统幅频特性 ∣ H ( j ω ) ∣ |H(j\omega)| ∣H(jω)∣ 和相频特性 θ ( ω ) \theta(\omega) θ(ω) 应如下图所示:
所以理想低通滤波器的频率响应函数 H ( j ω ) H(j\omega) H(jω) 可以表示为:
H ( j ω ) = { e − j ω t d , ∣ ω ∣ < ω C 0 , ∣ ω ∣ > ω C = g 2 ω C ( ω ) e − j ω t d H(j \omega)=\left\{\begin{array}{cl} \mathrm{e}^{-j \omega t_{d}}, & |\omega|<\omega_{C} \\ 0, & |\omega|>\omega_{C} \end{array}=g_{2 \omega_{C}}(\omega) \mathrm{e}^{-j \omega t_{d}}\right. H(jω)={e−jωtd,0,∣ω∣<ωC∣ω∣>ωC=g2ωC(ω)e−jωtd
其中 g 2 ω C ( ω ) g_{2 \omega_{C}}(\omega) g2ωC(ω) 表示自变量为 ω \omega ω ,以 0 0 0 为中心,以 2 ω C 2 \omega_{C} 2ωC 为宽度的门函数。
因此该理想低通滤波器的冲激响应 h ( t ) h(t) h(t) 为:
h ( t ) = F − 1 [ g 2 ω c ( ω ) e − j ω t d ] = ω c π S a [ ω c ( t − t d ) ] \begin{aligned} h(t) & =\mathrm{F}^{-1}\left[g_{2 \omega_{c}}(\omega) e^{-j \omega t_{d}}\right] \\ & =\frac{\omega_{c}}{\pi} \mathrm{Sa}\left[\omega_{c}\left(t-t_{d}\right)\right] \end{aligned} h(t)=F−1[g2ωc(ω)e−jωtd]=πωcSa[ωc(t−td)]
上述计算过程可以参考 真正掌握傅里叶变换 文章中门函数的傅里叶变换求解过程,再根据傅里叶变换的对称性可轻松求得。
截止角频率 ω C = 5 \omega_C=5 ωC=5 ,时移 t d = 1 t_d=1 td=1 时,对应的理想低通滤波器的冲激响应如下图所示:
你看,当输入为冲激函数 δ ( t ) \delta(t) δ(t) 时,这个滤波器的冲激响应 h ( t ) h(t) h(t) 竟然要求在输入之前就存在一部分( t < 0 t<0 t<0 时),这违背了因果性,因此说这是理想的低通滤波器,是不可能实现的。
从信号传输的角度来看,当传输信号的系统为理想低通滤波器时,冲激信号 δ ( t ) \delta(t) δ(t) 竟然失真成了理想低通滤波器的冲激响应 h ( t ) h(t) h(t) 的样子。这是因为 δ ( t ) \delta(t) δ(t) 的信号频带无限宽,而理想低通滤波器的通频带是有限的。
3. 物理可实现系统的条件
系统可物理实现有两个必要条件,第一个条件便是因果条件,也就是说因果系统才是物理可实现的系统。而因果系统的定义是:零状态响应不会出现在激励之前的系统,用公式表示为:
h ( t ) = 0 , t < 0 h(t)=0,\qquad t<0 h(t)=0,t<0
这个很好理解,比如我们要在空白的纸上记录一句话,不可能存在这种情况:正准备拿笔呢,这句话已经写了一半了;我们去食堂吃饭,打好菜准备吃之前,菜就已经有一部分进肚子里了。
第二个必要条件是系统的传输函数 H ( j ω ) H(j\omega) H(jω) 要满足佩利-维纳准则:
{ ∫ − ∞ ∞ ∣ H ( j ω ) ∣ 2 d ω < ∞ ∫ − ∞ ∞ ∣ ln ∣ H ( j ω ) ∣ ∣ / ( 1 + ω 2 ) d ω < ∞ \begin{cases} \int_{-\infty}^{\infty}|H(j \omega)|^{2} d \omega<\infty\\ \\ \int_{-\infty}^{\infty} \big|\ln | H(\mathrm{j} \omega)|\big|/({1+\omega^{2}}) \mathrm{~d} \omega<\infty \end{cases} ⎩⎪⎨⎪⎧∫−∞∞∣H(jω)∣2dω<∞∫−∞∞∣∣ln∣H(jω)∣∣∣/(1+ω2) dω<∞
这表明要想系统可以物理实现,可以允许 H ( j ω ) H(j\omega) H(jω) 特性在某些不连续的频率点上为0,但不允许在一个有限频带内为0(因为 H ( j ω ) H(j\omega) H(jω) 为0时,上述第二个式子的被积函数的分子部分 $ \big|\ln | H(\mathrm{j} \omega)|\big|$ 为无穷大)。按此原理,理想低通、理想高通、理想带通、 理想带阻等理想滤波器都是不可实现的。
注:本文首发于微信公众号"振动信号研究所"