issue4：model selection in frequentist and Bayesian

机器学习模型总会涉及到模型选择的问题，这是无法避而不见的。在一个模型的fitting function中，不仅存在parameter，还存在hyperparameter。一般来说，超参即是控制模型选择的一个方面。当然，模型选择还依赖于其他，例如在polynomial fitting curve中，不同的多项式的阶数也是模型选择的一个方面。

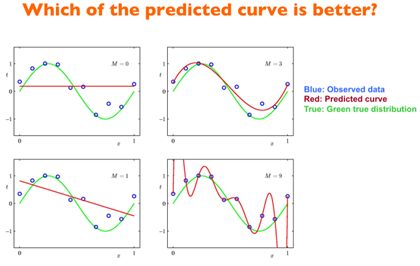
在上图中，我们已知产生训练数据的是一个正弦函数，所以3阶的选择显然是最好的。但是，一般情况下我们是无法观测到产生样本的分布，所以，如何选择模型是关乎准确性的重要方面。

我们最终的期望是，通过在训练集上得到一个fitting function，而这个函数在测试集上有很好的表现。首先，训练集上稍微overfitting一些，因为如果在训练集上效果都不好，那么迁移到测试集上岂不更差。但是不能使overfitting过于严重，如上图选取9阶多项式显然不会产生很好的效果。

对于多项式的curve fitting来讲，在确定阶数的情况下，可以通过限定参数空间大小避免过大的overfitting；在确定参数空间大小的时候，可以改变阶数获得不同的效果。

通常情况下，将数据集分为三部分（这里是粗浅的大分类）：

这基本上是所有工程问题都会遇到的。其中test set是为了测试fitting function的泛化能力而预留的，而validation set是为了调整超参预留的。

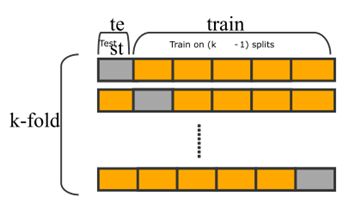
在工程上，为了保证调整的效果好，通常会做cross validation，而为了保证数据都能充分利用，有leave one out cross validation以及n-fold cross validation等。在libSVM的实现中，还用到了grid search去寻找最好的超参。下图中左右分别为LOOCV和n-fold CV：

但是在超参非常复杂的情况下，这种训练会耗尽很多计算资源，像grid search就是这样，基本上要在一个小范围内穷尽所有解。但grid search在大范围中使用了指数下降搜索的方法，会节省很多时间。

存在一些In-sample error estimate的方法，如AIC、BIC、MDL、SRM等。 其中M是自由参量的个数。通过增加自由参量的个数，可以增大似然度。但是似然度不能无限制增加，避免过拟合的出现。

Akaike Information Criteria：

其中D是数据集，是由最大使然估计时获得的最佳参数，M是参数可能存在的个数，即模型可能的个数。 【待验证】

Bayesian Information Criteria：

 

其中D是数据集，是由最大后验得到的最佳参数，相当于带有正则项的最大使然。N是训练数据个数，M是参数可能存在的个数。

关于BIC，可以使用laplace approximation的方法获得。具体内容在approximation一节中介绍。 【待补充】

Minimum Description Length Principal（不详细介绍）

Structural Risk Minimization（不详细介绍）

可以从贝叶斯的观点重新看待模型选择的问题。

从贝叶斯的观点来看待模型选择，由最大似然产生的overfitting可以通过边沿化（加和或者积分）模型参数来解决。这种方法把参数空间的大小看作一种不确定性，由概率表示。一旦边沿化去掉这一概率之后，模型选择的问题就自然解决了。

假设在观测数据上，我们一共有L个不同的模型，分别为。这里的模型指的是观测数据D上面不同的概率分布。假设数据是从L个模型中的某一个采样出来的，但是我们不知道具体是哪一个。可以使用先验概率表示为，这个先验概率表示数据从每个模型采样出来的可能性。给定一个数据集D，我们有

 

 

其中成为model evidence，它可以有如下表示：

 

意即数据D是在参数为w的模型上采样出来的，而参数w是在模型上采样出来的。易知，能够最大化这个概率的模型，才是最佳的模型，可以作为模型选择的结果。

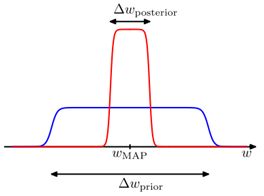
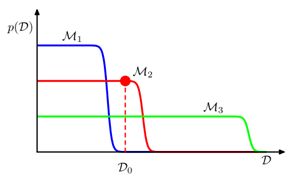
我们假设先验概率是非常扁平的，因为通常情况下我们不知道先验分布是什么样子的。而后验概率这是mode在MAP附近的钟型曲线，如下图：

则可以通过样条近似（微分法）把变化为，并采取对数形式，可得：

 

 

可以看出，前项是最大后验，即在当前模型下可以得到的最佳参数。而后项控制着模型复杂度。由于成立，所以后项的结果小于零。易知当后验可选择的范围非常大的时候，惩罚的力度就会加大，这种情况下就会限制后验的空间大小，这与带有regularization的频率派观点是相同的。

 

 

 

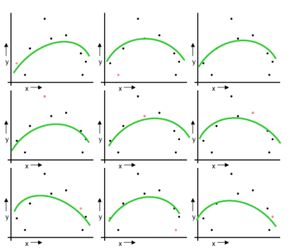
上图展示了三个具有不同模型复杂度拟合效果。随着数字的增长，三个模型复杂度随之加大。可见，简单的模型拟合能力很差，大于之后基本没有拟合能力，但是对于可以拟合的数据，给出最高的拟合概率，复杂的模型反之。

但是最大化model evidence的过程比较困难，因为这个过程是不可解析的，所以应使用近似的方法去求解。 【待求解】