强化学习Q-Learning算法

前言

学习这个算法有一段时间了，但是因为自己犯懒一直没有整理。现整理一下，一方面有刚入门的同学可以参考，另一方面哪里写错或者理解不深的还请大家及时指正。

基本概念

基本概念

首先列出一些强化学习中的基本概念，主要是为了帮助自己回忆起学习这个算法的过程。

1. 状态值函数：智能体在状态 $s$ 处的累计回报的期望值被称为智能在在采用策略 $\pi$ 时在状态 $s$ 处的状态值函数。用公式表示如下：$$v_{\pi }\left(s\right)=\mathbb{E}\left[\sum _{k=0}^{\infty }{\gamma }^k{\mathcal{R}}_{t+k+1}|S_t=s\right]$$
   不同的策略 $\pi$ 在相同的状态 $s$ 下对应的状态值函数是不同的，因为策略 $\pi$ 本身会影响智能体处在某一状态是的行为，进而改变累计回报 $\mathcal{G}$ 。
2. 状态-行为值函数：智能体在状态 $s$ 处执行动作 $a$ 所获得的累计回报的期望值被定义为智能体在策略 $\pi$ 时处在状态 $s$ 处执行动作 $a$ 的状态-行为值函数。用公式表示如下：$$q_{\pi }\left(s,a\right)={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{\mathcal{R}}_{t+k+1}|S_t=s,A_t=a\right]$$

递推关系

智能体的状态值函数和状态行为值函数之间存在一种递推关系。下图给出四种递推关系：

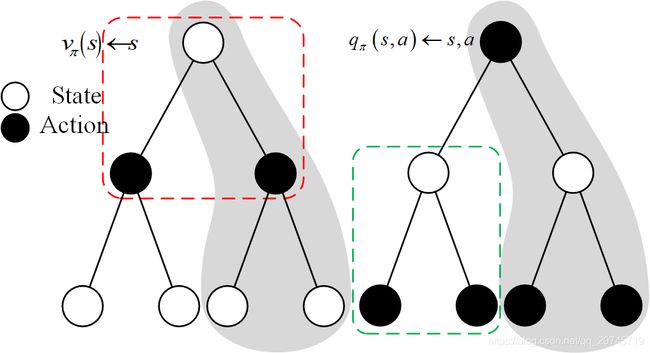
1. $v_{\pi }\left(s\right)\to q_{\pi }\left(s,a\right)$ $$v_{\pi }\left(s\right)=\sum _{a\in A}\pi \left(a|s\right)q_{\pi }\left(s,a\right)$$
2. $v_{\pi }\left(s\right)\to v_{\pi }\left(s^{\prime }\right)$$$v_{\pi }\left(s\right)=\sum _{a\in A}\pi \left(a|s\right)\left[R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }\left(s^{\prime }\right)\right]$$
3. $q_{\pi }\left(s,a\right)\to v_{\pi }\left(s^{\prime }\right)$$$q_{\pi }\left(s,a\right)=R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }\left(s^{\prime }\right)$$
4. $q_{\pi }\left(s,a\right)\to q_{\pi }\left(s^{\prime },a^{\prime }\right)$$$q_{\pi }\left(s,a\right)=R_s^a+\gamma \sum _{s^{\prime }}{P}_{s{s}^{\prime }}^a\left[\sum _{a^{\prime }\in A}\pi \left(s^{\prime }|a^{\prime }\right)q_{\pi }\left(s^{\prime },a^{\prime }\right)\right]$$

Q-learning基本原理

Q-Learning算法是一种基于表格的值函数迭代的强化学习算法。这个方法最大的特点就是建立一张Q值表(Q-Table)，算法迭代时Q值表不停地被更新，直至最后表中数据收敛。等到Q值表收敛后，智能体可以根据每个状态的行为值函数的大小来确定最优策略。Q值表示意如下：

$Q-Table$	$a_1$	$a_2$	$\cdots$	$a_m$
$s_1$	$q\left(s_1,a_1\right)$	$q\left(s_1,a_2\right)$	$q\left(s_1,\cdots \right)$	$q\left(s_1,a_m\right)$
$s_2$	$q\left(s_2,a_1\right)$	$q\left(s_2,a_2\right)$	$q\left(s_2,\cdots \right)$	$q\left(s_2,a_m\right)$
$⋮$	$q\left(\cdots ,a_1\right)$	$q\left(\cdots ,a_2\right)$	$\ddots$	$q\left(\cdots ,a_m\right)$
$s_n$	$q\left(s_n,a_1\right)$	$q\left(s_n,a_2\right)$	$q\left(s_n,\cdots \right)$	$q\left(s_n,a_m\right)$

智能体在探索时，按照下式的方式来更新Q-Table：
$$NewQ\left(s,a\right)=Q\left(s,a\right)+\alpha \underset{\Delta Q\left(s,a\right)}{R\left(s,a\right)+\gamma \underset{a^{\prime }\in A}{\max }Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)}$$

下面举一个例子来简单说明Q-Table的更新过程：
例：有一智能体，状态集合为$\left\{0,1\right\}$，动作集合为$\left\{+,-\right\}$，即时奖励$R\left(s,a\right)=-1$，折扣因子$\gamma =0.8$，学习率$\alpha =0.1$，环境的规则为：$0\stackrel{+}{}1$，$0\stackrel{-}{}0$，$1\stackrel{+}{}1$，$1\stackrel{-}{}0$，执行某一动作之后的状态转移概率是1，初始状态是0，初始化Q-Table为：

Q	+	-
0	0.0	0.0
1	0.0	0.0

智能体执行动作$+$之后，$Q\left(0,+\right)$会被更新为：
$$Q\left(0,+\right)=0.0+0.1\times \left[-1+0.8\max \left(Q\left(1,+\right),Q\left(1,-\right)\right)-0.0\right]=-0.1$$
进而Q-Table会被更新为：

Q	+	-
0	-0.1	0.0
1	0.0	0.0

注意事项

1. Q-Learning 是一个基于值函数迭代的方式，利用 Q 函数来寻找最优的 Action
2. 为了能够更好地更新 Q 值表，就需要更好地探索环境，因此需要多次执行随机策略以更好地“遍历”整个环境
3. 为了平衡探索与寻优，在经过一定回合的随机探索之后，需要智能体以一定的概率 ϵ 执行“最优”策略，并且 ϵ 应随着学习回合数的增加而增加
4. 算法收敛之后，也可以保持一定概率的探索，以防止陷入局部最优

局限性

Q-Learning算法是有自己的局限性的，主要体现在以下几点：

1. 当Q-Table的规模比较大时，算法迭代收敛时间非常长。
2. 如果智能体探索不充分，很有可能造成算法陷入局部最优。
3. 奖励函数设置如果不合理，很有可能陷入局部最优。
4. Q-Learning无法解决连续状态和连续动作的强化学习问题。

仿真

可以使用网上莫烦Python大神的代码，在OpenAI Gym下做仿真；也可以自己使用图形显示平台自己编写各种简单的仿真环境，然后编写代码测试。我使用的是OpenCV+PyTorch平台，代码一方面稍微有些长（因为还有绘图和调试程序），另一方面网上各种大神的代码，相比之下我的真的是没啥价值，如果有小伙伴想交流，可以私信。贴上一幅图，自己的仿真结果（Low得很…）。
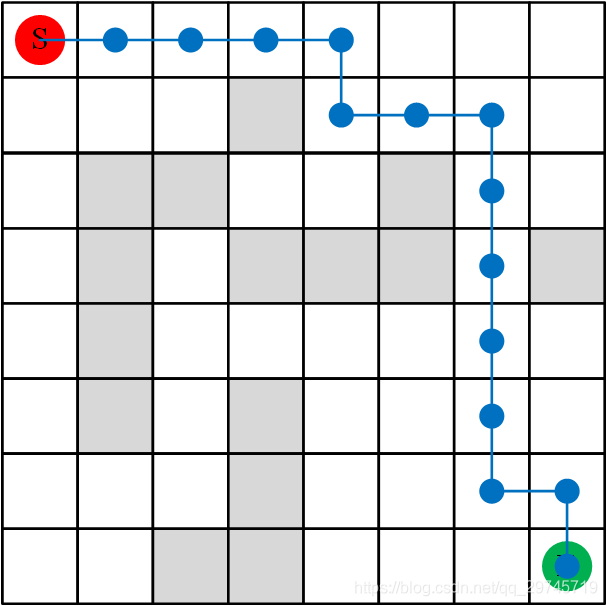迭代回合数：356
最优路径：$\left[0,0\right]\to \left[1,0\right]\to \left[2,0\right]\to \left[3,0\right]\to \left[4,0\right]\to \left[4,1\right]\to \left[5,1\right]\to \left[6,1\right]\to \left[6,2\right]\to \left[6,3\right]\to \left[6,4\right]\to \left[6,5\right]\to \left[6,6\right]\to \left[7,6\right]\to \left[7,7\right]$。