统计学习方法学习笔记-06-逻辑斯谛回归与最大熵模型01
首先介绍逻辑斯谛模型,然后介绍最大熵模型,最后讲述逻辑斯谛回归与最大熵模型的学习算法,包括改进的迭代尺度算法和拟牛顿法
逻辑斯谛回归模型
逻辑斯谛分布
设 X X X是连续随机变量,具有下列分布函数和密度函数: μ \mu μ是位置参数, γ > 0 \gamma \gt 0 γ>0是形状参数,越小,分布函数在中心增长得越快
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) / γ f ( x ) = F ′ ( x ) = e − ( x − μ ) / γ γ ( 1 + e − ( x − μ ) / γ ) 2 F(x) = P(X \leq x) = \frac{1}{1+e^{-(x - \mu) / \gamma}} \\ f(x) = F'(x) = \frac{e^{-(x - \mu) / \gamma}}{\gamma(1 + e^{-(x - \mu) / \gamma})^2} F(x)=P(X≤x)=1+e−(x−μ)/γ1f(x)=F′(x)=γ(1+e−(x−μ)/γ)2e−(x−μ)/γ
曲线如下:
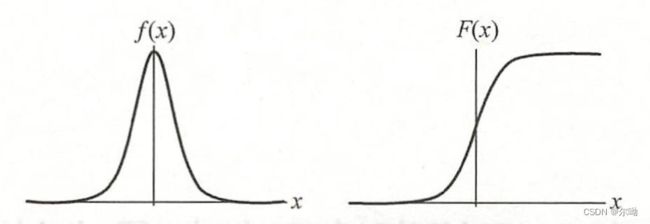
分布函数 F ( x ) F(x) F(x)是一条 S S S形曲线,该曲线以点 ( μ , 1 2 ) (\mu,\frac{1}{2}) (μ,21)为中心对称:
F ( − x + μ ) − 1 2 = − F ( x + μ ) + 1 2 F(-x + \mu) - \frac{1}{2} = -F(x + \mu) + \frac{1}{2} F(−x+μ)−21=−F(x+μ)+21
二项逻辑斯谛回归模型
- 二项逻辑斯谛回归模型是一种分类模型, x ∈ R n x \in R^n x∈Rn是输入, Y ∈ { 0 , 1 } Y \in \{0,1\} Y∈{0,1}, ω ∈ R n , b ∈ R \omega \in R^n,b\in R ω∈Rn,b∈R是参数, ω \omega ω是权值向量, b b b是偏置, ω ⋅ x \omega \cdot x ω⋅x是 ω , x \omega,x ω,x的内积
模型是如下的条件概率分布:
P ( Y = 1 ∣ x ) = e x p ( ω ⋅ x + b ) 1 + e x p ( ω ⋅ x + b ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( ω ⋅ x + b ) P(Y = 1|x) = \frac{exp(\omega \cdot x + b)}{1 + exp(\omega \cdot x + b)} \\ P(Y = 0|x) = \frac{1}{1 + exp(\omega \cdot x + b)} P(Y=1∣x)=1+exp(ω⋅x+b)exp(ω⋅x+b)P(Y=0∣x)=1+exp(ω⋅x+b)1 - 为了方便将权值向量和输入向量进行扩充: ω = ( ω ( 1 ) , ω ( 2 ) , ⋯ , ω ( n ) , b ) T , x = ( x ( 1 ) , x ( 2 ) , ⋯ , x ( n ) , 1 ) T \omega = (\omega^{(1)},\omega^{(2)},\cdots,\omega^{(n)},b)^T,x = (x^{(1)},x^{(2)},\cdots,x^{(n)},1)^T ω=(ω(1),ω(2),⋯,ω(n),b)T,x=(x(1),x(2),⋯,x(n),1)T,模型如下:
P ( Y = 1 ∣ x ) = e x p ( ω ⋅ x ) 1 + e x p ( ω ⋅ x ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( ω ⋅ x ) P(Y = 1|x) = \frac{exp(\omega \cdot x)}{1 + exp(\omega \cdot x)} \\ P(Y = 0|x) = \frac{1}{1 + exp(\omega \cdot x)} P(Y=1∣x)=1+exp(ω⋅x)exp(ω⋅x)P(Y=0∣x)=1+exp(ω⋅x)1 - 一个事件的几率:该事件发生与不发生的概率的比值 p 1 − p \frac{p}{1-p} 1−pp
- 该事件的对数几率是: l o g i t ( p ) = log p 1 − p logit(p) = \log \frac{p}{1-p} logit(p)=log1−pp
- 逻辑斯谛回归模型输出 Y = 1 Y = 1 Y=1的对数几率是 log P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = ω ⋅ x \log \frac{P(Y = 1|x)}{1 - P(Y = 1|x)} = \omega \cdot x log1−P(Y=1∣x)P(Y=1∣x)=ω⋅x,是输入 x x x的线性函数,通过逻辑斯谛回归模型可以将线性函数 ω ⋅ x \omega \cdot x ω⋅x转换为概率
模型参数估计
目的:逻辑斯谛回归模型学习 ω \omega ω的估计值,可以使用极大似然估计
给定训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T = \{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中 x i ∈ R n , y ∈ { 0 , 1 } x_i \in R^n,y \in \{0,1\} xi∈Rn,y∈{0,1}
设:
P ( Y = 1 ∣ x ) = π ( x ) , P ( Y = 0 ∣ x ) = 1 − π ( x ) P(Y = 1|x) = \pi(x),P(Y = 0|x) = 1 - \pi(x) P(Y=1∣x)=π(x),P(Y=0∣x)=1−π(x)
似然函数为:
∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i \prod_{i = 1}^N[\pi(x_i)]^{y_i}[1 - \pi(x_i)]^{1 - y_i} i=1∏N[π(xi)]yi[1−π(xi)]1−yi
对数似然函数为:
L ( ω ) = ∑ i = 1 N [ y i log π ( x i ) + ( 1 − y i ) log ( 1 − π ( x i ) ) ] = ∑ i = 1 N [ y i log π ( x i ) 1 − π ( x i ) + log ( 1 − π ( x i ) ) ] = ∑ i = 1 N [ y i ( ω ⋅ x i ) − log ( 1 + e x p ( ω ⋅ x i ) ) ] \begin{aligned} L(\omega) &= \sum_{i = 1}^N[y_i \log \pi(x_i) + (1 - y_i) \log (1 - \pi(x_i))] \\ &= \sum_{i = 1}^N\left[y_i\log \frac{\pi(x_i)}{1 - \pi(x_i)} + \log(1 - \pi(x_i))\right] \\ &= \sum_{i = 1}^N[y_i(\omega \cdot x_i) - \log(1 + exp(\omega \cdot x_i))] \end{aligned} L(ω)=i=1∑N[yilogπ(xi)+(1−yi)log(1−π(xi))]=i=1∑N[yilog1−π(xi)π(xi)+log(1−π(xi))]=i=1∑N[yi(ω⋅xi)−log(1+exp(ω⋅xi))]
对 L ( ω ) L(\omega) L(ω)求极大值,得到 ω \omega ω的估计值
问题转化为以对数似然函数为目标函数的最优化问题,可以采用梯度下降法及拟牛顿法
多项逻辑斯谛回归
此时离散型随机变量 Y Y Y的取值集合是 { 1 , 2 , ⋯ , K } \{1,2,\cdots,K\} {1,2,⋯,K},模型为:
P ( Y = k ∣ x ) = e x p ( ω k ⋅ x ) 1 + ∑ k = 1 K − 1 e x p ( ω k ⋅ x ) , k = 1 , 2 , ⋯ , K − 1 P ( Y = K ∣ x ) = 1 1 + ∑ k = 1 K − 1 e x p ( ω k ⋅ x ) P(Y = k|x) = \frac{exp(\omega_k \cdot x)}{1 + \sum_{k = 1}^{K - 1}exp(\omega_k \cdot x)},k = 1,2,\cdots,K-1 \\ P(Y = K|x) = \frac{1}{1 + \sum_{k = 1}^{K - 1}exp(\omega_k \cdot x)} P(Y=k∣x)=1+∑k=1K−1exp(ωk⋅x)exp(ωk⋅x),k=1,2,⋯,K−1P(Y=K∣x)=1+∑k=1K−1exp(ωk⋅x)1
x ∈ R n + 1 , ω k ∈ R n + 1 x \in R^{n + 1},\omega_k \in R^{n + 1} x∈Rn+1,ωk∈Rn+1
最大熵模型
最大熵模型由最大熵原理推导完成,首先叙述一般的最大熵原理,然后讲解最大熵模型的推导,最后给出最大熵模型学习的形式
最大熵原理
学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型,假设离散随机变量 X X X的概率分布是 P ( X ) P(X) P(X),其熵是:
H ( P ) = − ∑ x P ( x ) log P ( x ) H(P) = -\sum_xP(x)\log P(x) H(P)=−x∑P(x)logP(x)
熵满足 0 ≤ H ( P ) ≤ log ∣ X ∣ 0 \leq H(P) \leq \log |X| 0≤H(P)≤log∣X∣, ∣ X ∣ |X| ∣X∣是 X X X的取值个数,当 X X X的分布是均匀分布时右边的等号成立,也就是说 X X X服从均匀分布时熵最大;
直观的,最大熵原理认为要选择的概率模型首先必须满足已有的事实,即约束条件,在没有更多信息的情况下**,那些不确定的部分必须是等可能的,最大熵原理通过熵的最大化来表示等可能性**
最大熵模型的定义
假设分类模型是一个条件概率分布 P ( Y ∣ X ) , X ∈ X ⊆ R n P(Y|X),X \in \mathcal{X} \subseteq R^n P(Y∣X),X∈X⊆Rn表示输入, Y ∈ Y Y \in \mathcal{Y} Y∈Y表示输出, X , Y \mathcal{X},\mathcal{Y} X,Y分别是输入和输出的集合,这个模型表示的是对于给定的输入 X X X,以条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)输出 Y Y Y,训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T = \{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)},学习的目标是用最大熵原理选择最好的分类模型。
P ~ ( X = x , Y = y ) = ν ( X = x , Y = y ) N P ~ ( X = x ) = ν ( X = x ) N \tilde{P}(X = x,Y = y) = \frac{\nu(X = x,Y = y)}{N} \\ \tilde{P}(X = x) = \frac{\nu(X = x)}{N} P~(X=x,Y=y)=Nν(X=x,Y=y)P~(X=x)=Nν(X=x)
ν ( X = x , Y = y ) \nu(X = x,Y = y) ν(X=x,Y=y)表示的是训练样本中 ( x , y ) (x,y) (x,y)出现的频数, ν ( X = x ) \nu(X = x) ν(X=x)表示训练数据中输入 x x x出现的频数, N N N表示样本容量。
特征函数 f ( x , y ) f(x,y) f(x,y)描述输入 x x x和输出 y y y之间的某一个事实:
f ( x , y ) = { 1 x 和 y 满足某一事实 0 o t h e r w i s e f(x,y) = \begin{cases} 1 & x和y满足某一事实\\ 0 & otherwise \end{cases} f(x,y)={10x和y满足某一事实otherwise
特征函数 f ( x , y ) f(x,y) f(x,y)关于经验分布 P ~ ( X , Y ) \tilde{P}(X,Y) P~(X,Y)的期望值:
E P ~ ( f ) = ∑ x , y P ~ ( x , y ) f ( x , y ) E_{\tilde{P}}(f) = \sum_{x,y}\tilde{P}(x,y)f(x,y) EP~(f)=x,y∑P~(x,y)f(x,y)
特征函数 f ( x , y ) f(x,y) f(x,y)关于模型 P ( Y ∣ X ) P(Y|X) P(Y∣X)与经验分布 P ~ ( X ) \tilde{P}(X) P~(X)的期望值:
E P ( f ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) E_{{P}}(f) = \sum_{x,y}\tilde{P}(x)P(y|x)f(x,y) EP(f)=x,y∑P~(x)P(y∣x)f(x,y)
如果模型能获取训练数据中的信息,那么就可以假设这两个期望值相等
E P ~ ( f ) = E P ( f ) ∑ x , y P ~ ( x , y ) f ( x , y ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) E_{\tilde{P}}(f) = E_{{P}}(f) \\ \sum_{x,y}\tilde{P}(x,y)f(x,y) = \sum_{x,y}\tilde{P}(x)P(y|x)f(x,y) EP~(f)=EP(f)x,y∑P~(x,y)f(x,y)=x,y∑P~(x)P(y∣x)f(x,y)
我们将上式作为模型学习的约束条件,假如有 n n n个特征函数 f i ( x , y ) , i = 1 , 2 , ⋯ , n f_i(x,y),i = 1,2,\cdots,n fi(x,y),i=1,2,⋯,n,那么就有 n n n个约束条件
假设满足所有约束条件的模型集合为:
C ≡ { P ∈ P ∣ E P ( f i ) = E P ~ ( f i ) , i = 1 , 2 , ⋯ , n } \mathcal{C} \equiv \{P \in \mathcal{P}|E_P(f_i) = E_{\tilde{P}}(f_i),i = 1,2,\cdots,n\} C≡{P∈P∣EP(fi)=EP~(fi),i=1,2,⋯,n}
定义在条件概率分布上的条件熵为:
H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) H(P) = -\sum_{x,y}\tilde{P}(x)P(y|x) \log P(y |x) H(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)
集合模型 C \mathcal{C} C中条件熵 H ( P ) H(P) H(P)最大的模型称为最大熵模型
最大熵模型的学习(P100例题值得一看)
最大熵模型的学习过程就是求解最大熵模型的过程,最大熵模型的学习等价于约束最优化问题:
m a x P ∈ C H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) s . t . E P ( f i ) = E P ~ ( f i ) , i = 1 , 2 , ⋯ , n ∑ y P ( y ∣ x ) = 1 \mathop{max}\limits_{P \in \mathcal{C}}H(P) = -\sum_{x,y}\tilde{P}(x)P(y|x) \log P(y |x) \\ \begin{aligned} s.t. \ \ \ & E_P(f_i) = E_{\tilde{P}}(f_i),i = 1,2,\cdots,n \\ & \sum_{y}P(y|x) = 1 \end{aligned} P∈CmaxH(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)s.t. EP(fi)=EP~(fi),i=1,2,⋯,ny∑P(y∣x)=1
转化为等价的求最小值问题:
m i n P ∈ C − H ( P ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) s . t . E P ( f i ) − E P ~ ( f i ) = 0 , i = 1 , 2 , ⋯ , n ∑ y P ( y ∣ x ) = 1 \mathop{min}\limits_{P \in \mathcal{C}}-H(P) = \sum_{x,y}\tilde{P}(x)P(y|x) \log P(y |x) \\ \begin{aligned} s.t. \ \ \ & E_P(f_i) - E_{\tilde{P}}(f_i) = 0,i = 1,2,\cdots,n \\ & \sum_{y}P(y|x) = 1 \end{aligned} P∈Cmin−H(P)=x,y∑P~(x)P(y∣x)logP(y∣x)s.t. EP(fi)−EP~(fi)=0,i=1,2,⋯,ny∑P(y∣x)=1
将约束最优化的原始问题转换为无约束最优化的对偶问题,首先引进拉格朗日乘子 ω 0 , ω 1 , ω 2 , ⋯ , ω n \omega_0,\omega_1,\omega_2,\cdots,\omega_n ω0,ω1,ω2,⋯,ωn,定义拉格朗日函数 L ( P , ω ) L(P,\omega) L(P,ω):
L ( P , ω ) ≡ − H ( P ) + ω 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n ω i ( E P ~ ( f i ) − E P ( f i ) ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) + ω 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n ω i ( ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x , y P ~ ( x ) P ( y ∣ x ) f i ( x , y ) ) \begin{aligned} L(P,\omega) &\equiv -H(P) + \omega_0\left(1 - \sum_yP(y|x)\right) + \sum_{i = 1}^n\omega_i(E_{\tilde{P}}(f_i) - E_P(f_i)) \\ &= \sum_{x,y}\tilde{P}(x)P(y|x) \log P(y |x) + \omega_0\left(1 - \sum_yP(y|x)\right) + \sum_{i = 1}^n\omega_i\left(\sum_{x,y}\tilde{P}(x,y)f_i(x,y) - \sum_{x,y}\tilde{P}(x)P(y|x)f_i(x,y)\right) \end{aligned} L(P,ω)≡−H(P)+ω0(1−y∑P(y∣x))+i=1∑nωi(EP~(fi)−EP(fi))=x,y∑P~(x)P(y∣x)logP(y∣x)+ω0(1−y∑P(y∣x))+i=1∑nωi(x,y∑P~(x,y)fi(x,y)−x,y∑P~(x)P(y∣x)fi(x,y))
最优化的原始问题是:
m i n P ∈ C m a x ω L ( P , ω ) \mathop{min}\limits_{P \in \mathcal{C}} \mathop{max}\limits_{\omega} L(P,\omega) P∈CminωmaxL(P,ω)
对偶问题是:
m a x ω m i n P ∈ C L ( P , ω ) \mathop{max}\limits_{\omega} \mathop{min}\limits_{P \in \mathcal{C}} L(P,\omega) ωmaxP∈CminL(P,ω)
由于拉格朗日函数是 P P P的凸函数,原始问题的解与对偶问题的解是等价的
首先求解对偶问题内部的极小化问题 m i n P ∈ C L ( P , ω ) \mathop{min}\limits_{P \in \mathcal{C}} L(P,\omega) P∈CminL(P,ω), m i n P ∈ C L ( P , ω ) \mathop{min}\limits_{P \in \mathcal{C}} L(P,\omega) P∈CminL(P,ω)是 ω \omega ω的函数,将其记作
Ψ ( ω ) = m i n P ∈ C L ( P , ω ) = L ( P ω , ω ) \Psi(\omega) = \mathop{min}\limits_{P \in \mathcal{C}} L(P,\omega) = L(P_{\omega},\omega) Ψ(ω)=P∈CminL(P,ω)=L(Pω,ω)
将其解记作:
P ω = a r g m i n P ∈ C L ( P , ω ) = P ω ( y ∣ x ) P_\omega = arg \mathop{min}\limits_{P \in \mathcal{C}} L(P,\omega) = P_\omega(y|x) Pω=argP∈CminL(P,ω)=Pω(y∣x)
具体地,求 L ( P , ω ) L(P,\omega) L(P,ω)对 P ( y ∣ x ) P(y|x) P(y∣x)的偏导数
∂ L ( P , ω ) ∂ P ( y ∣ x ) = ( ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) + ω 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n ω i ( ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x , y P ~ ( x ) P ( y ∣ x ) f i ( x , y ) ) ) P ( y ∣ x ) ′ = ∑ x , y P ~ ( x ) ( 1 + log P ( y ∣ x ) ) + ∑ y ω 0 + ∑ x , y ( P ~ ( x ) ∑ i = 1 n ω i f i ( x , y ) ) = ∑ x , y P ~ ( x ) ( log P ( y ∣ x ) + 1 − ω 0 − ∑ i = 1 n ω i f i ( x , y ) ) \begin{aligned} \frac{\partial L(P,\omega)}{\partial P(y|x)} &= \left(\sum_{x,y}\tilde{P}(x)P(y|x) \log P(y |x) + \omega_0\left(1 - \sum_yP(y|x)\right) + \sum_{i = 1}^n\omega_i\left(\sum_{x,y}\tilde{P}(x,y)f_i(x,y) - \sum_{x,y}\tilde{P}(x)P(y|x)f_i(x,y)\right)\right)'_{P(y|x)} \\ &= \sum_{x,y}\tilde{P}(x)(1 + \log P(y |x)) + \sum_y\omega_0 + \sum_{x,y}\left(\tilde{P}(x)\sum_{i = 1}^n\omega_if_i(x,y)\right) \\ &= \sum_{x,y}\tilde P(x) \left( \log P(y|x) + 1 - \omega_0 - \sum_{i = 1}^n \omega_if_i(x,y)\right) \end{aligned} ∂P(y∣x)∂L(P,ω)=(x,y∑P~(x)P(y∣x)logP(y∣x)+ω0(1−y∑P(y∣x))+i=1∑nωi(x,y∑P~(x,y)fi(x,y)−x,y∑P~(x)P(y∣x)fi(x,y)))P(y∣x)′=x,y∑P~(x)(1+logP(y∣x))+y∑ω0+x,y∑(P~(x)i=1∑nωifi(x,y))=x,y∑P~(x)(logP(y∣x)+1−ω0−i=1∑nωifi(x,y))
令偏导数等于0,在 P ~ ( x ) > 0 \tilde P(x) \gt 0 P~(x)>0的情况下解得
P ( y ∣ x ) = e x p ( ∑ i = 1 n ω i f i ( x , y ) + ω 0 − 1 ) = e x p ( ∑ i = 1 n ω i f i ( x , y ) ) e x p ( 1 − ω 0 ) P(y|x) = exp \left( \sum_{i = 1}^n \omega_if_i(x,y) + \omega_0 - 1 \right) = \frac{exp \left( \sum_{i = 1}^n \omega_if_i(x,y) \right)}{exp(1 - \omega_0)} P(y∣x)=exp(i=1∑nωifi(x,y)+ω0−1)=exp(1−ω0)exp(∑i=1nωifi(x,y))
由于 ∑ y P ( y ∣ x ) = 1 \sum_y P(y|x) = 1 ∑yP(y∣x)=1:
P ω ( y ∣ x ) = 1 Z ω ( x ) e x p ( ∑ i = 1 n ω i f i ( x , y ) ) P_\omega(y|x) = \frac{1}{Z_\omega(x)}exp \left( \sum_{i = 1}^n \omega_if_i(x,y) \right) Pω(y∣x)=Zω(x)1exp(i=1∑nωifi(x,y))
其中: Z ω ( x ) Z_\omega(x) Zω(x)被称为规范化因子
Z ω ( x ) = ∑ y e x p ( ∑ i = 1 n ω i f i ( x , y ) ) Z_\omega(x) = \sum_yexp \left( \sum_{i = 1}^n \omega_if_i(x,y) \right) Zω(x)=y∑exp(i=1∑nωifi(x,y))
P ω = P ω ( y ∣ x ) P_\omega = P_\omega(y|x) Pω=Pω(y∣x)就是最大熵模型
之后将求解得到的最大熵模型带到拉格朗日函数中得到包含 ω \omega ω的函数,求关于 ω \omega ω的极大化问题,分别对 ω 1 , ω 2 , ⋯ , ω n \omega_1,\omega_2,\cdots,\omega_n ω1,ω2,⋯,ωn求导,令偏导数为0求出 ω \omega ω的值,将得出的 ω \omega ω值带到最大熵模型中得到最大熵模型的结果。