机器学习模型度量方法，分类及回归模型评估

如何度量模型的性能

对于分类和回归两类监督学习，分别有各自的评判标准
分类：预测的变量的离散的
回归：预测的变量的连续的

一、分类模型的评估

在对比不同模型的能力时，使用不同的性能度量时往往会导致不同的判断结果。因为不同的度量指标侧重点不同。

1. 准确率/精度（Accuracy）、查准率 / 精确率（Precision）、查全率 / 召回率（Recall）

对于二分类问题：

查准率表现为预测为正的样本中有多少是真的正样本
查全率表现为所有真的正样本中到底有多少被检测出来。

查准率和查全率的应用场景：

在审判犯罪嫌疑人时，我们希望司法系统的查准率越高越好，即尽量不要冤枉无辜者，因为误判为正样本的后果很严重；

对于银行的欺诈检测系统来说，通常希望它的查全率越高越好，即尽量把欺诈账户识别出来，因为漏检会带来很大损失，而误判为正样本则影响不大。

这意味着模型的好坏是相对的，什么样的模型是好的，不仅取决于算法和数据，还取决于任务需求。

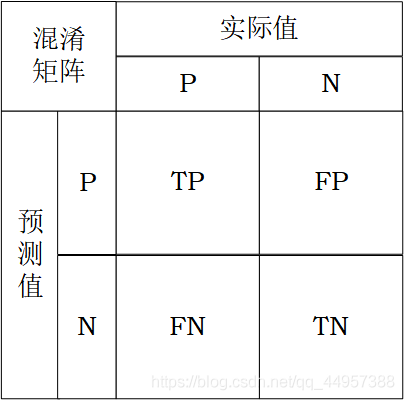
2. 混淆矩阵

混淆矩阵的每一列代表预测值，每一行代表的是实际类别。
这个名字来源于它可以非常容易的表明多个类别是否有混淆（一个class被预测成另一个class）。

对于二分类：

对于多分类：

假设有一个用来对Dog、Cat、Tiger进行分类的系统，混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27只动物：3只狗， 6只猫， 12只老虎。预测结果的混淆矩阵如下图：

实际有12只老虎，有3只被误判成狗，4只被误判成猫

所有正确的预测结果都在对角线上，所以从混淆矩阵中可以很方便直观的看出哪里有错误。

3. $F1$和$F\beta$

$F1$基于查准率与查全率的调和平均定义的，更接近于两个数较小的那个，所以查准率和查全率接近时，$F1$值最大。

$\frac{2}{F1}=\frac{1}{Precision}+\frac{1}{Recall}$

在一些应用中，对查准率和查全率的重视程度有所不同，因此就有了$F\beta$，$F\beta$是基于查准率与查全率的加权调和平均

$F\beta =\frac{(1+{\beta }^2)\ast Precision\ast Recall}{{\beta }^2\ast Precision+Recall},\beta >0$

$\beta$表示查全率对查准率的相对重要性。

$\beta =1$时，退化为标准的$F1$；$\beta >1$时，查全率有更大的影响；$\beta <1$时，查准率有更大的影响。

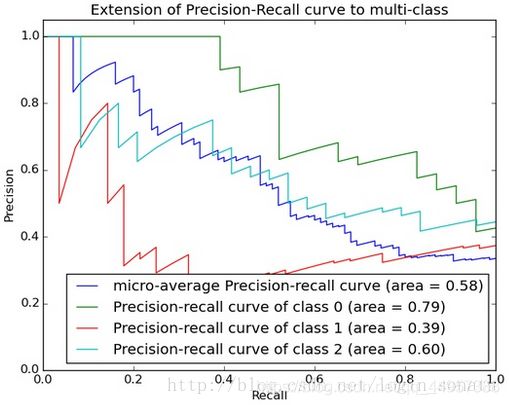
4. PR曲线

PR曲线的横坐标是查准率，纵坐标是查全率

PR曲线越光滑越好（中间两根蓝色的好），上边的比下边的好（绿线比红线好）。

当比较两个模型的优劣时，有时PR曲线会相交，因此为了直观反映哪个模型更好，常常要用$F1$或$F\beta$比较，针对不同的场景，有不同的评价标准。

如上图，当查准率和查全率的值接近时，$F1$值最大，此时画连接$(0,0)$和$(1,1)$的直线，直线和PR曲线重合的地方的$F1$，是这条PR曲线最大的$F1$

PR曲线的下面积为平均精度(AP)，它是PR曲线的积分，用来评估目标检测模型的性能。一个越好的分类器，AP值越高。

现在来看看改变阈值对查全率和查准率的影响

很多学习器对样本的预测是生成一个实值或概率值，并设定一个分类阈值，然后将预测值与该阈值进行比较，大于阈值的为正类，小于阈值为负类。

在不同的应用任务中，我们可根据任务需求采用不同的阈值。

如果我们增大这个阈值，大于阈值的正类样本和负类样本都会变少，小于阈值的正类样本和负类样本都会变多。

大于阈值的正类样本 对应 正确预测的正类(TN)，其变少，所以查全率降低

大于阈值的负类样本 对应 被误判为正类的样本(FP)，变少了，大于阈值的样本 对应 所有预测为正类的样本(TN+FP)，也变少了且下降的更快，所以查准率提高

类似的，如果我们减小这个阀值，查全率提高，查准率降低。

一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

即真正例率和假正例率随阈值的改变趋势相反，所以PR曲线是向下的。

PR曲线的意义在于，可以直观看出查准率随着查全率增大的变化。如果曲线越接近右上角，就说明随着Recall的增加，Precision往下掉的速度不明显。这说明如果需要的话，可以调整阈值以增加Recall，而不用担心Precision掉的太厉害。

5. ROC曲线

横坐标是“假正例率”（FPR），纵坐标是“真正例率”（TPR，即查全率）

FPR反映模型把负例预测为正例的能力

TPR反映模型把正例预测为正例的能力

ROC曲线越光滑越好，越靠近左上角越好

阈值确定时，FP（大于阈值的负类样本）和TP（大于阈值的正类样本）也确定了。

所以对于每个分类器，一定的阈值对应一定的真正例率和假正例率，即ROC曲线上的一个点，将不断改变阈值得到的点链接起来，就得到ROC曲线。

现在来看看改变阈值对真正例率和假正例率的影响

如果我们增大阈值，大于阈值的正类样本和负类样本都会变少

大于阈值的正类样本 对应 预测正确的正类，其变少，真正例率下降

大于阈值的负类样本 对应 被误判为正类的样本，其变少，假正例率下降

类似的，如果我们减小阀值，真正例率和假正例率都提高。

即真正例率和假正例率随阈值的改变趋势相同，所以ROC曲线是向上的。

阈值最大为1，所有样本被预测为负，对应ROC曲线的$(0,0)$
阈值最小为0，所有样本被预测为正，对应ROC曲线的$(1,1)$

一般情况下，ROC曲线都应该处于$(0,0)$和$(1,1)$连线的上方。

ROC和PR：

ROC曲线兼顾正例和负例的权衡。因为TPR聚焦于正例，FPR聚焦于负例。PR曲线的两个指标查准率和查全率都聚焦于正例。

在实际的数据集中经常会出现类不平衡现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同。当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变，而PR曲线会变化很大。

当正负样本数量差距不大的情况下，ROC和PR的趋势是差不多的，但是在正负样本分布极不均衡的情况下，PR比ROC更能真实的反映出实际情况，因为此时ROC曲线看起来似乎很好，但是在PR上却效果一般。

PR曲线和ROC曲线应用场景：

• ROC曲线适用于评估分类器的整体性能，以及需要剔除类别不平衡影响的情况；而PR曲线适用于评估更看重正例的情况。

• 如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响，则ROC曲线比较适合。

• 在信息检索、推荐中，希望Precision较大，用户希望排名靠前的推荐是自己想要的结果，所以评估时PR曲线比较合适。

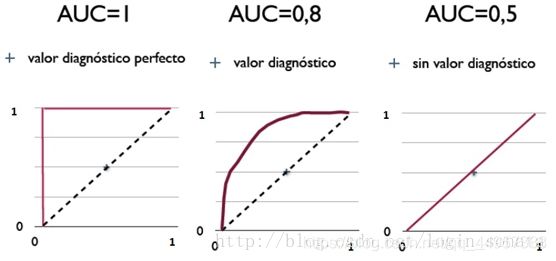
6. AUC值

AUC（Area Under Curve）被定义为ROC曲线下的面积(ROC的积分)，通常在0.5 - 1之间。

ROC曲线越靠近左上角，AUC值越大，分类器的性能越好。

AUC评价：

AUC = 1，采用这个预测模型时，不管设定什么阈值都能完全准确预测。绝大多数预测的场合，不存在这种分类器。

0.5 < AUC < 1，优于随机猜测。这个分类器设定合适的阈值，能有预测价值。

AUC = 0.5，跟随机猜测一样（例：丢硬币），模型没有预测价值。

AUC < 0.5，比随机猜测还差；但总是反预测，就优于随机猜测，因此不存在AUC < 0.5的情况。

二、回归模型的评估

回归算法的模型评估与分类算法的模型评估不同，在分类算法中，评判是否预测到了正确的分类；在回归算法中，评判是否预测到了正确的数值、以及是否拟合到了足够的信息。

1. 平均绝对误差MAE（Mean Absolute Error）
   
   缺点：虽然MSE能获得一个评价值，但是你并不知道这个值代表模型拟合是优还是劣，只有通过对比才能达到效果。

2. 平均平方误差MSE（Mean Squared Error）

   这也是线性回归中最常用的损失函数
   

3. 均方根误差（RMSE）

   由于MSE与我们的目标变量的量纲不一致，为了保证量纲一致性，我们需要对MSE进行开方
   
   缺点：平均误差对异常值比较敏感，异常值的出现会使RMSE的误差较大（如果有一个预测值与真实值相差很大，RMSE就会很大）。

4. $R^2$(决定系数)

   $R^2$判断的是预测模型和真实数据的拟合程度，最佳值为1，可为负值。
   
   其中，$f(x_i)$为真实标签，$y_i$为预测结果，$\overline{y_i}$为样本均值。

• 分母为原始数据的离散程度，方差。

• 分子为预测数据和原始数据的误差，残差平方和，即模型没有拟合到的信息。

• 两者相除可以消除原始数据离散程度的影响。

  如果$R^2$是0，说明模型没有拟合能力，预测值都是 $\overline{y_i}$

  如果$R^2$是1，说明模型预测完全正确。

  总之，$R^2$越接近1，表明这个模型对数据拟合的越好；$R^2$越接近0，表明模型拟合的越差

  缺点：数据集的样本越大，R²越大，因此，不同数据集的模型结果比较会有一定的误差

sklearn自带的回归模型评估指标

mean_absolute_error(y_true, y_pred) #MAE

mean_squared_error(y_true, y_pred[, …]) #MSE

r2_score(y_true, y_pred[, …]) #R^2

explained_variance_score(y_true, y_pred) #可解释方差

mean_squared_log_error(y_true, y_pred) #均值平方对数误差

median_absolute_error(y_true, y_pred) #中位数绝对误差

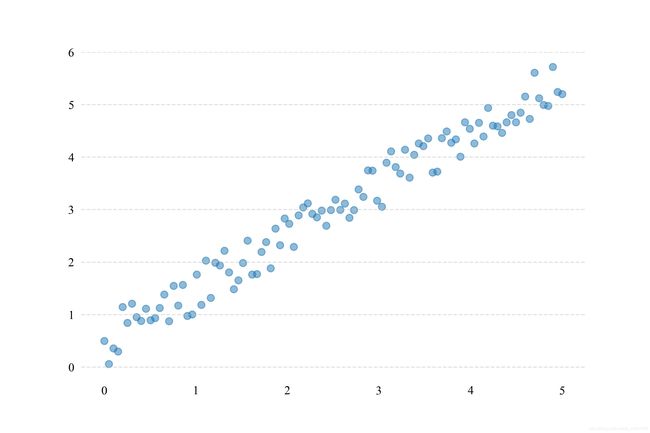
下面是一些样本点

下面的三条线，分别对应三个回归模型的结果

可以看出，红色的线拟合效果比较好，紫色的线没有拟合能力，绿色的线最差

下面是红色的线对应模型的几种评估结果：

mean_absolute_error(y_true,y_pred1)#平均绝对误差

结果：0.24248035286300917

mean_squared_error(y_true,y_pred1)#均方误差

结果：0.07919872929290986

r2_score(y_true,y_pred1)

结果：0.9633942147205354

下面是绿色的线对应模型的几种评估结果：

mean_absolute_error(y_true,y_pred2)#平均绝对误差

结果：2.5184719922947116

mean_squared_error(y_true,y_pred2)#均方误差

结果：8.498868923661782

r2_score(y_true,y_pred2)

结果：-2.9281914459419114