基于R语言一元线性回归模型实例及代码

题目描述

所用数据集——faithful(MASS包)

# 加载数据包及查看问题背景
library(MASS)
data("faithful")
?data

Waiting time between eruptions and the duration of the eruption for the Old Faithful geyser in Yellowstone National Park, Wyoming, USA.
（美国怀俄明州黄石国家公园老忠实间歇泉喷发之间的等待时间和喷发持续时间。）
Format
A data frame with 272 observations on 2 variables.
[,1] eruptions numeric Eruption time in mins
[,2] waiting numeric Waiting time to next eruption (in mins)
Details
A closer look at faithful$eruptions reveals that these are heavily rounded times originally in seconds, where multiples of 5 are more frequent than expected under non-human measurement.

数据特征及可视化

可视化(visualization)在统计里是重要的，随着计算工具的进步，对于一个未知模型，先利用图像进行直观感受不失为一种有效的方法，这个过程也能讲你积累的统计直觉充分发挥出来，进而启发你选择恰当的模型。相反，数据特征的作用并不是很大，广泛来说。方差展示稳定性，均值展示一般水平，但，然后呢？
这里强烈推荐的是plot(dataset),因为这道题只有两个变量，所以输出结果只有一张散点图，我们换一个数据集试试

library(MASS)
data("iris")
plot(iris)

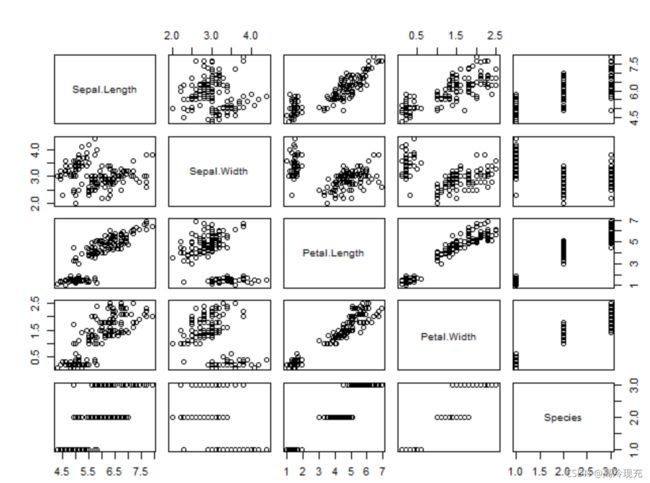
这个数据集里一共5个变量，故理论上有5*5张图，但自己与自己是没意义的，减去5张，y与x的散点图和x与y的散点图是对称的，也就剪掉一半，实际上只剩10张图，对于这个数据集来说，有效的图其实更少，我们可以看到有些图尽是一些横线或竖线，这是因为里面有个变量是分类变量，最后我们只需看6张图。为了方便叙述，我们用坐标$(x,y),x,y\in \{1,2,3,4,5\}$表示我们要说的图，可以看到$(1,2)$是比较杂乱的，图$(3,4)$呈上升带状，说明 Petal.Length和 Petal.Width 有明显的正相关关系。对于其他图，有一条上升带状，并且有明显的分类，具体的造成原因就得联系问题背景等进行下一步的探索。
OK，回到原题目，我们把图画出来

明显的正相关函数，顺其自然地，我们考虑最简单的一元线性模型

建立模型与初步评价

通过可视化，我们决定尝试下面模型
$$\mathrm{e}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}={\beta }_0+{\beta }_1\cdot \mathrm{w}\mathrm{a}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}+\epsilon$$
利用R自带的lm()得到模型，summary是个强大而实用的函数，可以对我们的模型进行各方面的考察，学会解读summary出来的结果，是十分重要的

model=lm(faithful$eruptions~faithful$waiting)
summary(model)
# 得到结果如下

Call:
lm(formula = eruptions ~ waiting)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.29917 -0.37689  0.03508  0.34909  1.19329 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.874016   0.160143  -11.70   <2e-16 ***
waiting      0.075628   0.002219   34.09   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4965 on 270 degrees of freedom
Multiple R-squared:  0.8115,	Adjusted R-squared:  0.8108 
F-statistic:  1162 on 1 and 270 DF,  p-value: < 2.2e-16

我们的结论是：从 $p$ 值来看，截距项和一次项系数都是显著的，没有充分理由拒绝接受最小二乘得到的拟合值。拟合优度为0.8108，不算很高。由 $F$ 检验的结果，可以认为方程在 $p=0.05$ 的水平上通过整体的显著性检验，我们接受这个模型的假设

（自己写lm()代码）

建议初学者可以自行尝试一下
如果用的是这样的形式，在算参数的估计值时我们可以先中心化数据，这里只给出计算参数的部分

myownlm <- function(x,y){
  if(!is.vector(x)) x=as.vector(x)
  if(!is.vector(y)) y=as.vector(y)
  x1=x-mean(x)
  beta1<-(t(x1)%*%y)/(t(x1)%*%x1)
  beta0<-mean(y)-beta1*mean(x)
  result<-c(beta0,beta1)
  return(result)
}

而我采用的形式是
$$Y=X\beta +\epsilon$$
这样算其实并不快，主要我学习的参考书是这种模型，后续章节也是以这种形式出现，我们需要构造这样的矩阵：第一列全为1，第二列才是数据包里的waiting数据

myownlm <- function(x,y,x.pred){
  if(!is.vector(x)) x=as.vector(x)
  if(!is.vector(y)) y=as.vector(y)
  if(!is.numeric(x.pred))x.pred=as.vector(x.pred)
  free=length(x)-2
  # 构造第一列为1的X
  x_temp=c(1:length(x))*0+1
  x=matrix(c(x_temp,x),ncol=2)
  # 利用公式（*）
  beta=solve(t(x)%*%x)%*%t(x)%*%y
  return(beta)
}

(*)：$\beta =(X^{\mathbf{T}}X{)}^{-1}{X}^{\mathbf{T}}Y$

显著性检验

整体显著性检验

数学理论

这个地方有点难度，首先我们得先介绍约束最小二乘，其实就是在原本的回归线性假设下加上一个约束 $A\beta =b$，$\beta$ 最后的形式这里不赘述，但我们需要意识到加了约束后产生的影响：$\beta$ 的变化范围减小，因而残差平方和 $RS{S}_H$ 变大，于是总有 $RS{S}_H\ge RSS$

一般线性假设，对于正态线性回归模型，$y=X\beta +e,e\sim N(0,{\sigma }^{2}I),X\in {\mathbb{R}}^{n\times p},\beta \in {\mathbb{R}}^{p\times 1}（1）$,我们的对参数的检验问题可写为 $H:A\beta =b,A\in {\mathbb{R}}^{m\times p}(2)$
我们有以下结论：
(a) $RSS/{\sigma }^2\sim {\chi }_{n-p}^2$
(b) 若（2）假设成立，则 $\frac{(RS{S}_H-RSS)}{{\sigma }^2}\sim {\chi }_m^2$
(c ) $RSS\perp RS{S}_H$
(d) (2)成立时，
$$F_H=\frac{(RS{S}_H-RSS)/m}{RSS/(n-p)}\sim F_{m,n-p}\text{\hspace{1em}(*)}$$
证明过程略

所谓整体显著性检验，就是检验假设：所有的回归系数为0，即检验
$$H:{\beta }_1=\cdots ={\beta }_{p-1}=0\text{\hspace{1em}(3)}$$
将（1）写成分量形式
$$y_i={\beta }_0+x_{i1}+\cdots +x_{i,p-1}{\beta }_{p-1}+e_i,e_i\sim N(0,{\sigma }^2),i=1,\cdots ,n\text{\hspace{1em}(4)}$$
关键的一点来了：把（3）看成是（2）的一种特殊情形，我们就能将这个检验带回到我们约束最小二乘时的检验，此时有
$$A=(0I_{p-1}),b=0$$
将（3）代入（4），有
$$y_i={\beta }_0+e_i,i=1,\cdots ,n$$
此时 ${\beta }_0$的最小二乘估计为 $\bar{y}$,容易算得对应得残差平方和为
$$RS{S}_H=y^{\prime }y-{\beta }_0^{\ast }{1}^{\prime }y=\sum _{i=1}^n(y_i-\bar{y}{)}^2$$
而由残差分解式，我们知道 $TSS=RSS+S{S}_{回}$，检验统计量可改写为
$$F_H=\frac{S{S}_{回}/m}{RSS/(n-p)}\sim F_{m,n-p}$$

系数显著性检验

参数矩阵 $\beta$得最小二乘估计为 $\hat{\beta }=(X^{\prime }X{)}^{-1}{X}^{\prime }y$，由 $e\sim N(0,{\sigma }^{2}I)$，可以容易推出 $\hat{\beta }\sim N(\beta ,{\sigma }^2(X^{\prime }X{)}^{-1})$，若记 $C_{p\times p}=(c_{ij})=(X^{\prime }X{)}^{-1}$，则有
$${\hat{\beta }}_i\sim N({\beta }_i,{\sigma }^2{c}_{ii})$$
假如我们的假设检验为
$$H_i:{\beta }_i=p$$
若假设成立，则有，${\hat{\beta }}_i-p\sim N(0,{\sigma }^2{c}_{ii})$，此时构造检验统计量
$$\frac{{\hat{\beta }}_i-p}{\sigma \sqrt{c_{ii}}}\sim N(0,1)$$
但 $\sigma$是未知的，利用 ${\hat{\sigma }}^2=RSS/(n-p)$以及 $RSS$与 ${\hat{\beta }}_i$独立的事实，进而构造t统计量
$$t_i=\frac{{\hat{\beta }}_i}{\hat{\sigma }\sqrt{c_{ii}}}\sim t_{n-p}$$
对给定的置信水平 $\alpha$，当 $|t_i|>t_{n-p}(\frac{\alpha }{2})$时拒绝原假设，否则接受，或者说没有充分理由拒绝

代码实现系统显著性检验

关于整体显著性检验，实际上，summary里面的F-statistic就是做这个用的。
下面我们来判断是否接受 ${\beta }_1=0.05$的假设，给出代码如下(有些在之前就赋值了，完整代码见附录)

free=270
x_temp=c(1:length(waiting))*0+1
x=matrix(c(x_temp,waiting),ncol=2)
y=eruptions
y.fit=result[1]+result[2]*waiting 
sigma.estimate=sqrt(sum((y-y.fit)*(y-y.fit))/free)
c_ii=solve(t(x)%*%x)[2,2]
t_1=(result[2]-0.05)/(sqrt(c_ii)*sigma.estimate)
t_1
if(abs(t_1)>qt(1-0.05/2,df=free)){print("Refused")
}else{print("accept")}

回归诊断

利用最小二乘估计得到的参数建立在数据的误差$\epsilon$服从正态分布的假设前提下。回归诊断有两方面的工作，第一就是通过残差量验证我们的拟合模型是否符合 $\mathbf{G}\mathbf{a}\mathbf{u}\mathbf{s}\mathbf{s}-\mathbf{M}\mathbf{a}\mathbf{r}\mathbf{k}\mathbf{o}\mathbf{v}$假设，称为残差分析；第二就是探查对参数估计或预测有异常大的影响的数据。
首先我们画出残差图，(代码放在最后),一是看散点是否大部分落在[-2,2]之间，而是看散点的分布是否均匀，是否会呈现漏斗状之类的

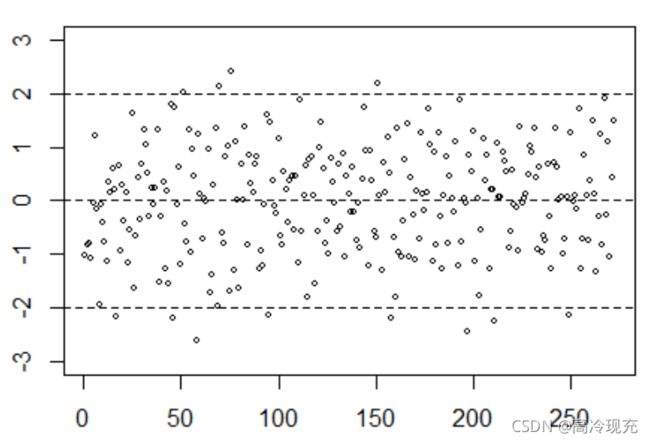
可以看到，学生化残差图的结果还是令人满意的，但这仅仅是我们的直观感受，它的比较好的作用在于当图像呈现其他趋势时，其趋势对我们接下来做数据变换往往具有启发性。所以，我们要量化我们的主观感受，对残差做一次shapiro检验

> shapiro.test(rstudent)

	Shapiro-Wilk normality test

data:  rstudent
W = 0.9927, p-value = 0.2035

我们接受 $\mathbf{G}\mathbf{a}\mathbf{u}\mathbf{s}\mathbf{s}-\mathbf{M}\mathbf{a}\mathbf{r}\mathbf{k}\mathbf{o}\mathbf{v}$假设

异常点检验

使用Cook统计量，具体内容不介绍

Cook=rstudent*(h_ii/(1-h_ii))/2
plot(c(1:272),Cook,type='h',xlab = "waiting",ylab = "Cook")
title(main = "Cook Statictis")
abline(0,0)
# 异常点的数量自己规定，也不一定非得10个，剔除太多对原始数据影响太大，太少又没有达到优化目的
ordercook=order(abs(Cook),decreasing = TRUE)[1:10]
points(as.vector(ordercook),Cook[ordercook])
# 找到异常点的索引
> ordercook
 [1] 158 265 161 197 203 242 160 269  66 170

也可以用R自带的函数进行检验，画出来的图像更美观

模型预测

在R中实用predict()对新的变量进行预测，这里有一个很坑的地方必须提一下

predict(model,data.frame(waiting=80),interval = "confidence")
predict(model,data.frame(waiting=80),interval = "prediction")

如果这里不小心写成

predict(model,data.frame(x=80),interval = "confidence")

你将会看见诡异的结果如下：

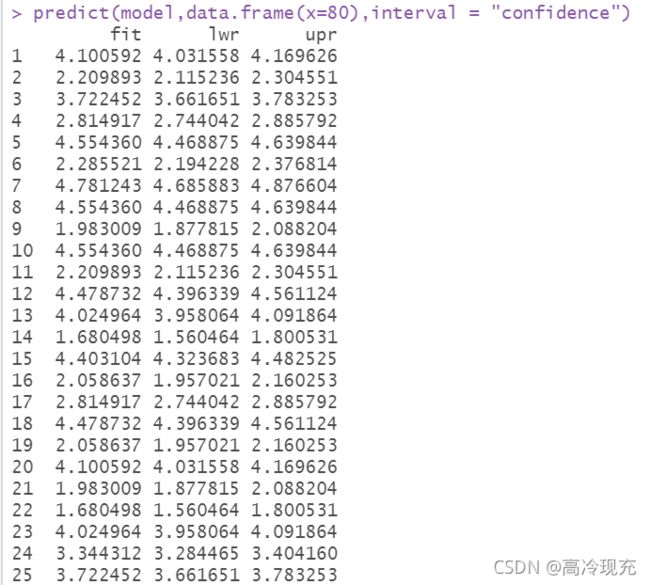
这是因为predict()识别不了x，你要把自变量完完整整的名字还给它。如果写成x，他会认为你没有要预测的值，进而把原来数据集的数据按照model拟合一遍，给出的结果正是原有数据的拟合值。这个问题看似不容易犯，但要是没经验搞错了，很难察觉是名字的原因。

我们在刚刚的myownlm基础上修改一下，直接上代码

myownlmnew <- function(x,y,x.pred){
  if(!is.vector(x)) x=as.vector(x)
  if(!is.vector(y)) y=as.vector(y)
  if(!is.numeric(x.pred))x.pred=as.vector(x.pred)
  free=length(x)-2
  x_temp=c(1:length(x))*0+1
  x=matrix(c(x_temp,x),ncol=2)
  beta=solve(t(x)%*%x)%*%t(x)%*%y
  x.pred=c(1,x.pred)
  y.pred=t(x.pred)%*%beta
  y.fit=x%*%beta
  sigma.estimate=sqrt(sum((y-y.fit)*(y-y.fit))/free)
  temp=t(x.pred)%*%solve(t(x)%*%x)%*%x.pred
  temp1=qt(1-0.05/2,df=free)*sigma.estimate*sqrt(temp)
  temp2=qt(1-0.05/2,df=free)*sigma.estimate*sqrt(1+temp)
  result=data.frame(intercept=beta[1],slope=beta[2],pred=y.pred,
                    confidence_lwr=c(y.pred-temp1),confidence_upr=c(y.pred+temp1),
                    prediction_lwr=c(y.pred-temp2),prediction_upr=c(y.pred+temp2))
  return(result)
}

后记

这只是一个简单的例子，文章对于数据的处理方法也很基础。事实上，这些方法都是灵活的，没有那么好的事，说某种模型就是最好的，要是这样，我们的世界该是多么单纯啊。拟合模型的使用目的是做预测，但不是对原数据得拟合度越高，这个模型就越有用，既然追求无限接近于1的模型，直接用很高阶的函数或者傅里叶变换不就得了，直接等于1，但是这样的模型有用吗？它是没用的。关于回归的学习还有很多，有兴趣的人还是得学好基础，不要误用滥用。

附录

完整R代码

library(MASS)
data("faithful")
?data

eruptions=faithful$eruptions
waiting=faithful$waiting
plot(x=waiting,y=eruptions,cex=0.8,xlab = "Waiting",ylab = "Eruptions")

cor(faithful)

mean(eruptions)
mean(waiting)
var(eruptions)
var(waiting)
median(eruptions)
median(waiting)
max(eruptions)-min(eruptions)
max(waiting)-min(waiting)

library(ggplot2)
p=ggplot(data=faithful,aes(x=waiting))
p+geom_histogram(bins=35)

# myownlm()
myownlm <- function(x,y){
  if(!is.vector(x)) x=as.vector(x)
  if(!is.vector(y)) y=as.vector(y)
  x1=x-mean(x)
  beta1<-(t(x1)%*%y)/(t(x1)%*%x1)
  beta0<-mean(y)-beta1*mean(x)
  result<-c(beta0,beta1)
  return(result)
}
# 运行结果
result=myownlm(waiting,eruptions)
result

summary(lm(eruptions~waiting))

plot(x=waiting,y=eruptions,cex=0.8,xlab = "Waiting",ylab = "Eruptions")
abline(result[1],result[2])

y.fit=result[1]+result[2]*waiting
RSS=sum((eruptions-y.fit)*(eruptions-y.fit))
TSS=sum((eruptions-mean(eruptions))*(eruptions-mean(eruptions)))
SS_re=sum((y.fit-mean(eruptions))*(y.fit-mean(eruptions)))

myownlmnew <- function(x,y,x.pred){
  if(!is.vector(x)) x=as.vector(x)
  if(!is.vector(y)) y=as.vector(y)
  if(!is.numeric(x.pred))x.pred=as.vector(x.pred)
  free=length(x)-2
  x_temp=c(1:length(x))*0+1
  x=matrix(c(x_temp,x),ncol=2)
  beta=solve(t(x)%*%x)%*%t(x)%*%y
  x.pred=c(1,x.pred)
  y.pred=t(x.pred)%*%beta
  y.fit=x%*%beta
  sigma.estimate=sqrt(sum((y-y.fit)*(y-y.fit))/free)
  temp=t(x.pred)%*%solve(t(x)%*%x)%*%x.pred
  temp1=qt(1-0.05/2,df=free)*sigma.estimate*sqrt(temp)
  temp2=qt(1-0.05/2,df=free)*sigma.estimate*sqrt(1+temp)
  result=data.frame(intercept=beta[1],slope=beta[2],pred=y.pred,
                    confidence_lwr=c(y.pred-temp1),confidence_upr=c(y.pred+temp1),
                    prediction_lwr=c(y.pred-temp2),prediction_upr=c(y.pred+temp2))
  return(result)
}

result2=myownlmnew(waiting,eruptions,80)
result2

model=lm(eruptions~waiting)
predict(model,data.frame(waiting=80),interval = "confidence")
predict(model,data.frame(waiting=80),interval = "prediction")

free=270
x_temp=c(1:length(waiting))*0+1
x=matrix(c(x_temp,waiting),ncol=2)
y=eruptions
y.fit=-1.87402+0.07563*waiting 
sigma.estimate=sqrt(sum((y-y.fit)*(y-y.fit))/270)
c_ii=solve(t(x)%*%x)[2,2]
t_1=0.05/(sqrt(c_ii)*sigma.estimate)
t_1
if(abs(t_1)>qt(1-0.05/2,df=free)){print("Refused")
}else{print("accept")}

error=y-y.fit
sigma.estimate=sqrt(sum((y-y.fit)*(y-y.fit))/free)
H=x%*%solve(t(x)%*%x)%*%t(x)
h_ii=as.vector(diag(H))
rstudent=error/(sigma.estimate*sqrt(1-h_ii))
plot(c(1:272),rstudent,main="Residual Diagram",cex=0.6,xlab = "waiting",ylim = c(-3,3),ylab = "error(student)")
abline(h=c(-2,0,2),lty=2)
Cook=rstudent*(h_ii/(1-h_ii))/2
plot(c(1:272),Cook,type='h',xlab = "waiting",ylab = "Cook")
title(main = "Cook Statictis")
abline(0,0)
ordercook=order(abs(Cook),decreasing = TRUE)[1:10]
points(as.vector(ordercook),Cook[ordercook])
shapiro.test(rstudent)